A peste negra foi uma das mais devastadoras pandemias na história da humanidade. Segundo algumas estimativas, terá dizimado cerca de um terço da população da Europa e da Ásia no século XIV. Tendo surgido pela primeira vez em Portugal em 1348, a peste foi recorrente no nosso país até finais do século XVII. Em Inglaterra, o último grande surto de peste ocorreu nos anos de 1665/1666 e ficou conhecido como a Grande Peste de Londres.

Vitimou cerca de 15% dos habitantes da capital inglesa. O facto de se terem registado e mantido estatísticas semanais de mortalidade fornece-nos informação essencial sobre a progressão da doença (FIGURA 2). John Graunt (1620-1674) utilizou-as para analisar os dados e tirar várias conclusões sobre a epidemia, registadas no seu livro Natural and Political Observations Made Upon the Bills of Mortality (Observações naturais e políticas baseadas nos registos de mortalidade), que conheceu cinco edições.

O primeiro resultado em epidemiologia matemática que se conhece é devido a Daniel Bernoulli (1700-1782), filho e sobrinho de dois matemáticos famosos, Johann e Jakob. Daniel formou-se em medicina, tendo-se posteriormente dedicado à matemática. Em 1760, apresentou à Academia das Ciências de Paris uma memória intitulada Essai d’une nouvelle analyse da la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir (Ensaio de uma nova análise da mortalidade causada pela varíola e das vantagens da inoculação para a impedir), onde defendia, recorrendo a um modelo matemático, a inoculação contra a varíola (FIGURA 3).

No século XX, outra devastadora pandemia dizimou 3 a 5% da população mundial: a gripe pneumónica de 1918. Estima-se que cerca de 500 milhões de pessoas tenham sido infetadas, um quinto das quais terá sucumbido. A guerra na Europa favoreceu a propagação da doença, não só pelas condições de insalubridade a que os soldados estavam sujeitos, mas também pelas deficiências de nutrição sofridas pelas populações durante o conflito. Mais próximas e ainda bem presentes na memória podemos referir a pandemia de SIDA, surgida na década de 80 do século passado, a gripe A (H1N1) em 2009/2010 e o surto de ébola de 2014-2016. Exemplos de doenças infeciosas causadas por coronavírus são a MERS (Middle Eastern Respiratory Syndrome) com surto em 2012, causada por MERS-CoV, a SARS (Severe Acute Respiratory Syndrome) de 2002-2004, causada por SARS-CoV-1 e a atual COVID-19, causada por SARS-CoV-2.

Os alicerces da moderna abordagem à epidemiologia matemática foram lançados por A.G. McKendrick (1876-1943) e W.O. Kermack (1898-1970) em três artigos publicados em 1927, 1932 e 1933^{1, 2}. Partindo de suposições relativamente simples, o seu modelo mostrava um comportamento similar ao observado em muitas epidemias, como a peste negra ou a gripe: aparecimento súbito, crescimento rápido e desaparecimento, ficando parte da população incólume.

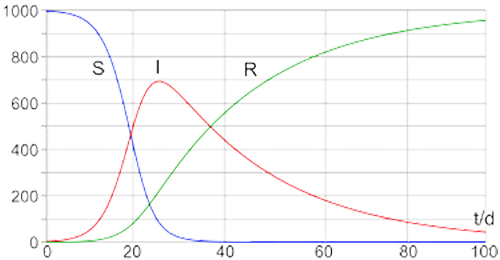
O modelo proposto por McKendrick e Kermack dividia uma população fechada de \(N\) indivíduos em três compartimentos: \(S\) – suscetíveis, \(I\) – infeciosos e \(R\) – recuperados. Admitia um número de contactos suficientes para que um indivíduo transmitisse a infeção a βN elementos por unidade de tempo, recuperando os indivíduos infetados a uma taxa \(γI\) por unidade de tempo. A dinâmica do modelo \(SIR\) é dada pelo sistema de equações diferenciais da FIGURA 5. O correspondente diagrama de fluxo é \(S\underset{\beta }{\rightarrow}I\underset{\gamma }{\rightarrow}R\).

Numa população inicialmente suscetível, um indivíduo infecioso transmitirá a doença a uma taxa de \(βN\) num período \(1_{\gamma }\), infetando assim \(R_{0}=\beta N_{/\gamma }\) indivíduos em média. \(R_{0}\) diz-se o número básico de reprodução e determina a dinâmica da epidemia: se R0 > 1 a epidemia propaga-se, se \(R_{0}<1\) a epidemia extingue-se. Compreende-se intuitivamente que se o indivíduo transmite a infeção a menos de um elemento em média, então o número de casos terá de decrescer com o tempo.

O gráfico da FIGURA 5 ilustra a evolução de uma epidemia modelada pelo modelo \(SIR\). A população suscetível (linha azul) diminui à medida que o número de infetados (linha vermelha) aumenta até atingir um pico e começar a diminuir. Esta diminuição verifica-se porque há uma diminuição do número de suscetíveis e um aumento do número de recuperados (linha verde).

\(\frac{dS}{dt}=-\beta SI\)

\(\frac{dI}{dt}=\beta SI-\gamma I\)

\(\frac{dR}{dt}=\gamma I\)

Os modelos compartimentais deterministas podem, de um modo geral, ser dados por uma equação vetorial da forma \(\frac{dX}{dt}=F\left ( X \right )\), onde \(X=\left ( X_{1}\left ( t \right ),X_{2}\left ( t \right ),...,X_{n}\left ( t \right ) \right )\) e \(F\left ( X \right )=\left ( F_{1}\left ( X \right ),\left ( X \right ),...,F_{n}\left ( X \right ) \right )\).

No caso particular do modelo SIR descrito acima temos \(n=3,X=\left ( S\left ( t \right ),I\left ( t \right ),R\left ( t \right ) \right ),F_{1}\left ( S,I,R \right )=\beta SI,F_{2}\left ( S,I,R \right )=\beta SI-\gamma I\) e \(F_{3}\left ( S,I,R \right )=\gamma I\).

Observe-se que é possível reduzir o sistema em uma equação se considerarmos uma população de dimensão \(N\) constante.

Há situações nas quais um modelo mais simples que o \(SIR\) pode ser adequado. O modelo \(SI\) , com apenas dois compartimentos (\(n=2\)), no qual os indivíduos suscetíveis, uma vez infetados assim permanecem, serve como modelo do herpes. Tem como solução a conhecida curva logística. O modelo \(SIS\), também com dois compartimentos, no qual os indivíduos infetados não adquirem imunidade, voltando a ficar suscetíveis após a infeção, ilustra o que sucede nos casos de constipação ou de gripe. É também possível determinar uma solução analítica explícita para este modelo. A inclusão de mais ou menos compartimentos permite modelar diferentes situações e realçar aspetos que se julgue importante incluir na modelação. A um aumento do grau de complexidade corresponderá um maior número de compartimentos na qual está dividida a população em estudo. Não existem soluções analíticas para os modelos mais elaborados, sendo necessário recorrer a simulações computacionais. O método de Euler, por exemplo, permite obter as soluções numéricas das equações diferenciais no caso dos modelos deterministas.

A erradicação da varíola, certificada em 1979, foi declarada pela Organização Mundial de Saúde (OMS) em 1980. Tal foi possível graças a extensas campanhas de vacinação e ao facto de ser necessário imunizar apenas cerca de 75% da população para se atingir a imunidade de grupo, um valor baixo se comparado, por exemplo, com os 93% necessários para o sarampo. (Sobre isto veja-se o parágrafo 7 do artigo Modelo \(SIR\) em epidemiologia, de João Nuno Tavares, publicado no número de junho de 2017 desta mesma revista³, onde o autor discute vários aspetos matemáticos do modelo.) Existem, no entanto, algumas amostras de vírus da varíola armazenadas em laboratório, para fins de investigação, o que levanta receios de que possa ser utilizado como arma biológica num ataque terrorista. A libertação do vírus numa população quase completamente suscetível teria efeitos devastadores, porventura semelhantes aos da COVID-19. Consequentemente, são ainda estudados vários modelos para a varíola, nos quais se incluem medidas de controlo como, por exemplo, a vacinação⁴. Um modelo possível é o \(SEIR\): aos três compartimentos do \(SIR\) acrescenta-se um quarto, \(E\), para os indivíduos expostos, que estão infetados mas ainda não transmitem a doença. Apesar da sua simplicidade e do reduzido número de equações (\(n=4\)), o modelo ajusta-se bem aos dados históricos que se possuem sobre os surtos de varíola.

Os modelos compartimentais podem também ser usados na modelação das chamadas doenças endémicas, doenças que persistem numa determinada região e em que o surgimento de novos casos se dá sem importação de infeções exteriores à população. Atualmente, o dengue é um dos graves problemas de saúde pública com que a sociedade se defronta. Doença infeciosa transmitida principalmente pela fêmea do mosquito Aedes aegypti, é endémica em mais de 100 países e estima-se que cerca de 55% da população mundial esteja em risco de a contrair. O primeiro surto em Portugal ocorreu na ilha da Madeira em 2012. Desde 2016 que está licenciado em vários países o uso de uma vacina desenvolvida pelo laboratório francês Sanofi Pasteur, tendo a OMS recomendado, à altura do lançamento da vacina no mercado, a sua utilização para indivíduos entre os 9 e os 45 anos de idade em países onde a doença fosse altamente endémica.

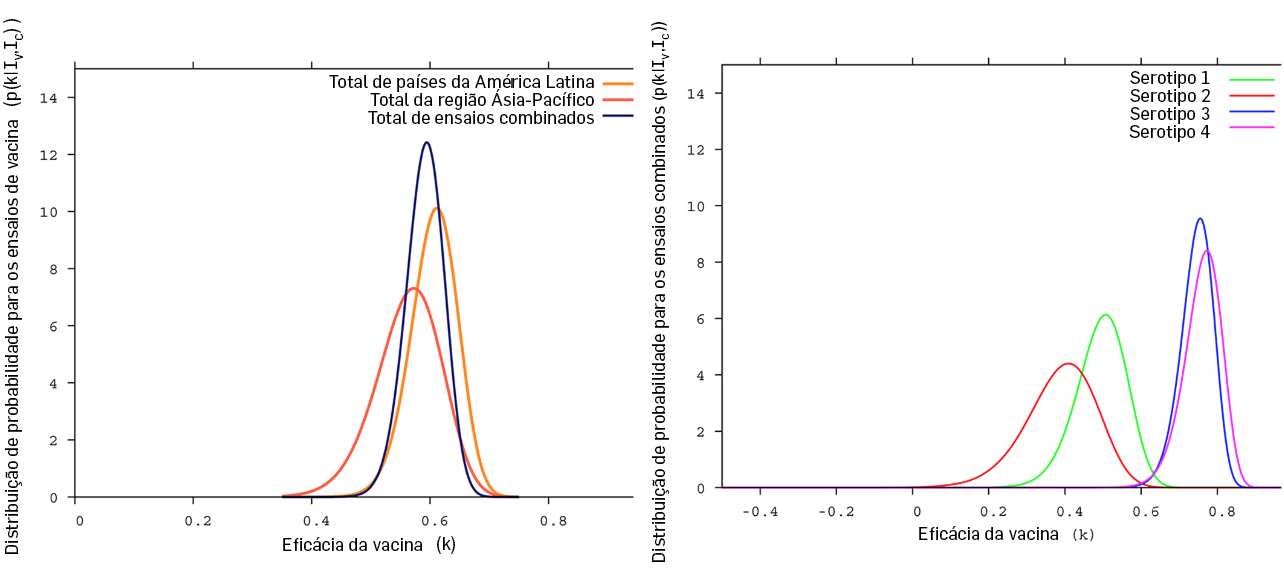
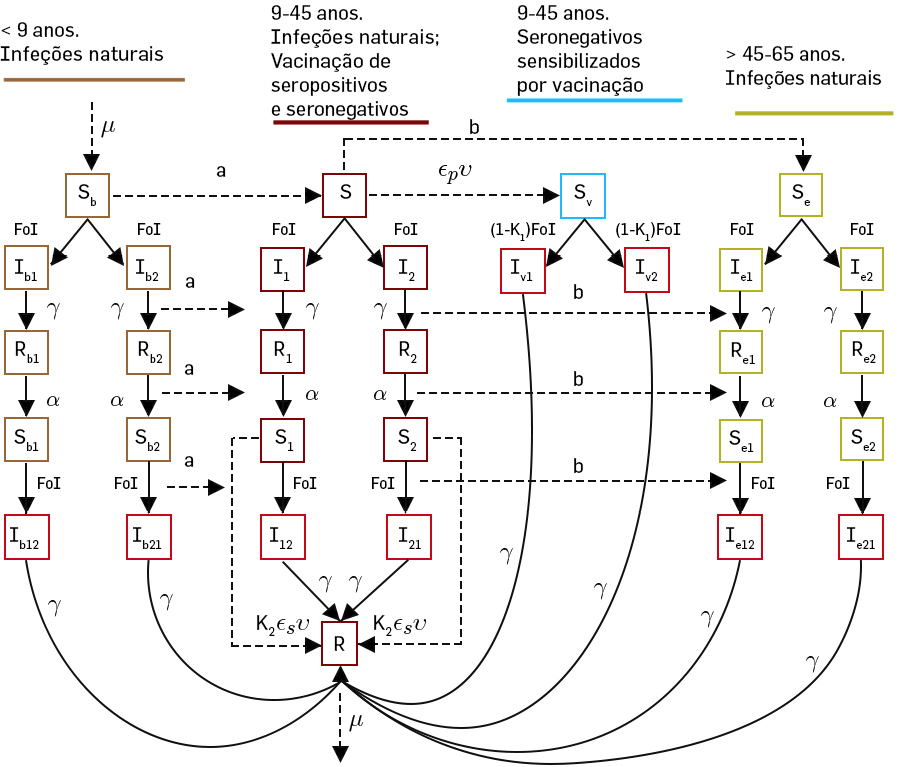
Os resultados estatísticos dos ensaios clínicos publicados foram reproduzidos em Portugal (FIGURA 6), tendo os investigadores analisado os riscos inerentes àquela recomendação. Usando um modelo de tipo \(SIR\) com estrutura etária, com 33 equações diferenciais (\(n=33\)), cujo diagrama se apresenta na FIGURA 7, concluíram que a eficácia da vacina e o risco relativo de hospitalização após inoculação depende da condição serotípica do indivíduo e não da sua idade⁵. Em 2018, a OMS alterou as suas orientações, passando a recomendar a vacina apenas para indivíduos que já tenham tido contacto com a doença ou para maiores de 9 anos em populações altamente endémicas.

A modelação matemática pode ser feita com recurso a outras técnicas, como as estocásticas ou as estatísticas. Por exemplo, observando os dados oficiais disponíveis, uma análise cuidadosa mostrou que a sazonalidade desempenha um papel importante na transmissão do dengue no Brasil, sendo a densidade de casos residual durante o inverno no hemisfério sul (meados de junho a meados de setembro). Assim, foi possível concluir não ser provável que os adeptos de futebol fossem infetados durante o Mundial de 2014 que decorreu naquele país, o que de facto se verificou⁶.

A modelação matemática em epidemiologia tem como objetivo, não só compreender a evolução da doença e os mecanismos subjacentes à sua dinâmica, mas também: fazer previsões quanto à progressão e duração da epidemia, ao número de infetados e ao número de mortos; estimar vários parâmetros epidemiológicos como, por exemplo, a taxa de infeção, o número básico de reprodução e a taxa de letalidade; analisar de que modo a adoção de medidas de controlo como o distanciamento social ou a vacinação podem afetar a progressão da epidemia.

Nada disso é fácil enquanto decorre um surto, sobretudo quando está em causa uma nova doença acerca da qual muito se desconhece, como sucede com a COVID-19. Inúmeros fatores dificultam a estimação de parâmetros fundamentais para a modelação matemática e nos resultados dos modelos a fiabilidade numérica dos parâmetros é crucial para a validação dos mesmos. Veja-se o exemplo da taxa de letalidade, definida como a razão entre o número de óbitos causados pela doença e o número total de infetados. Existem grandes diferenças nas políticas de testagem, não só entre os diversos países, como nas diferentes fases da doença. Numa fase inicial, a escassez de testes levou a que fossem testados apenas os casos sintomáticos suspeitos. A consequente subestimação do número total de infetados enviesa a estimação da taxa de letalidade. Atualmente, vários grupos trabalham na modelação da COVID-19. Muitos estarão certamente a analisar modelos do tipo \(SIR\), com mais ou menos compartimentos consoante os aspetos da doença que julguem importante evidenciar. Não será exagero afirmar que nem Kermack nem McKendrick podiam imaginar a importância que o seu modelo viria a adquirir quando o publicaram há quase cem anos.