Em 1772, o astrónomo alemão Johann Daniel Titius (FIGURA 1), em Wittenberg, redigiu uma carta ao colega Johann Elert Bode (FIGURA 2), em Berlim, onde mostrava uma relação interessante entre as distâncias médias dos planetas em relação ao Sol. Esta relação permitia determinar as posições médias expressas em unidades astronómicas dos planetas conhecidos desde a Antiga Babilónia até então, ou seja, Mercúrio até Saturno (recorde-se que uma unidade astronómica, ua, corresponde à distância média entre a Terra e o Sol, e é sensivelmente igual a 149 600 000 km, ou seja, aproximadamente 150 milhões de km).

De facto, Bode adotou rapidamente esta fórmula, sem fazer referência ao seu autor, e argumentou que deveria existir um planeta à distância de 2,8 ua, algures entre Marte e Júpiter. Com efeito, só em 1801, Giuseppe Piazzi, da Sicília, encontrou o primeiro asteroide, denominado Ceres, da hoje conhecida Cintura de Asteroides, entre Marte e Júpiter, precisamente a uma distância de 2,8 ua em relação ao Sol. De facto, esta cintura de asteroides parece ter resultado da desintegração de um planetoide que, por via do forte campo gravitacional de Júpiter, não conseguiu manter-se estável.

Devido ao entusiasmo nesta relação que, aparentemente, explicava as distâncias médias dos planetas em relação ao Sol, procurou-se descobrir outros planetas para outros termos dessa sequência, ou seja, além de Saturno. Assim, foi através desta fórmula empírica que William Herschal descobriu Urano, o primeiro planeta a ser detetado com recurso a um telescópio, em 1781, na distância prevista pela mesma. Este facto reforçou a “validade” da mesma e a fórmula passou a ser designada por lei.

Todavia, existiam perturbações na órbita de Urano cuja origem permanecia desconhecida. De facto, apesar de corretamente se poder considerar o conjunto de efeitos gravitacionais de Júpiter e Neptuno sobre Urano, este não seria suficiente para explicar as observações. Uma vez que a lei empírica de Titius-Bode previa com bastante precisão os planetas até Urano e a cintura de astertoides, o astrónomo inglês John Coach Adams e o alemão Urbain Jean Joseph Leverrier propuseram a existência de um planeta adicional, o que poderia solucionar o problema. Com efeito, em 1846, foi descoberto um oitavo planeta no Sistema Solar – Neptuno, pelo astrónomo inglês Johann Gottfried Galle. Contudo, o desvio entre a distância real medida e a prevista pela lei de Titius-Bode era muito grande, traduzindo-se num erro de cerca de 27%. Surge então inevitavelmente a questão: deixaria esta lei de ser válida?

Com a descoberta posterior de Plutão, em 1930 pelo astrónomo inglês Clyde W. Tombaugh, a diferença foi mais evidente, o que revelava um erro gigante de cerca de 96%¹.

Assim, apesar da coincidência da previsão com as distâncias reais da maioria dos planetas do Sistema Solar, esta relação empírica deixou de ser válida devido às enormes discrepâncias com Neptuno e Plutão, ainda que este último seja um planeta anão.

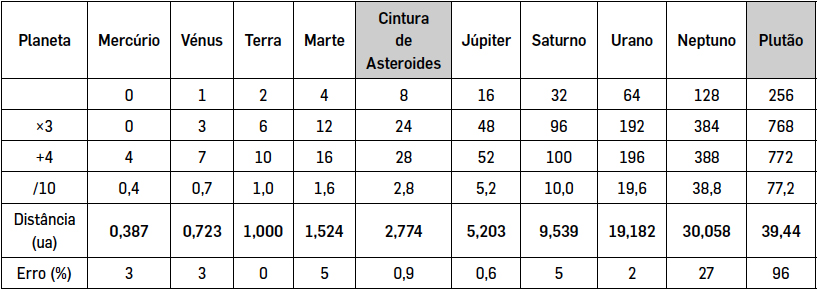
Não deixando de ser apenas uma feliz coincidência para alguns planetas, esta relação merece ser explorada de seguida com algum pormenor. Passemos, então, a ver em concreto esta lei de Titius-Bode, que é uma lei empírica que parte de uma progressão de razão 2 a partir do segundo termo, sendo que o primeiro é zero e onde, seguidamente, algumas operações simples são efetuadas, como a multiplicação por três, a adição de quatro unidades e a divisão por dez, exemplificadas na TABELA 1.

Na realidade, cada termo da série, após o primeiro, pode ser dado pela fórmula: \(d_{n}=\frac{3\times 2^{n}+4}{10}\), em que \(n= 0, 1, 2, 3, 4, ...\). Podemos, inclusive, admitir que o primeiro termo corresponde ao limite \(\underset{n\rightarrow -\infty }{lim}d_{n}\), o que leva à crítica levantada por Carl Frederich Gauss de que implicaria existir uma miríade de planetas entre Mercúrio e Vénus, uma vez que os inteiros negativos também deveriam estar presentes na fórmula. Também uma outra observação merece atenção: será que Plutão deveria ocupar a posição de Neptuno na fórmula, uma vez que a distância de Plutão de 39,44 ua está muito mais próxima do valor previsto para \(n=7\) na fórmula anterior? Isso implicaria que Neptuno tivesse sido capturado pelo Sistema Solar após a sua formação de tal modo que a sua interação gravitacional houvesse afastado Plutão da sua órbita inicial. Contudo, esta argumentação não parece ser verosímil à luz dos dados atuais, em que Plutão não apresenta as características para ser planeta principal, mas sim um planeta anão.

De facto, o entusiasmo na relação de Titius-Bode ainda persiste, de tal modo que novas formulações daquela têm sido avançadas com o intuito de aproximar as previsões das observações, tais como, por exemplo, os trabalhos de Blagg², Richardson³ e Ragnarsson⁴; apesar de não existirem motivos de natureza física mais profunda para a veracidade da lei e de não ser válida para Neptuno e para o planeta anão Plutão. Na realidade, esta relação pode ser encarada como a situação análoga à geometrização do Universo no modelo geocêntrico de esferas concêntricas de Ptolomeu que, apesar de belo esteticamente e de descrever alguns fenómenos, não correspondia à realidade, nem explicava todos as observações. Assim, esta regra empírica é amplamente aceite como curiosidade científica.