Descrição do problema

Um avião voa com uma velocidade \(V\), superior à velocidade do som, \(S\). Em cada instante, o motor do avião emite um som que se propaga no espaço, com velocidade \(S\), em todas as direções, sob a forma de ondas esféricas — estas esferas chamam-se as frentes de onda. Quando atingem o solo, intersetam-no em círculos cujo raio vai crescendo à medida que o tempo avança. Se um habitante da região sobrevoada pelo avião estiver dentro destes círculos, ele ouvirá o ruído dos motores do avião.

Objetivo

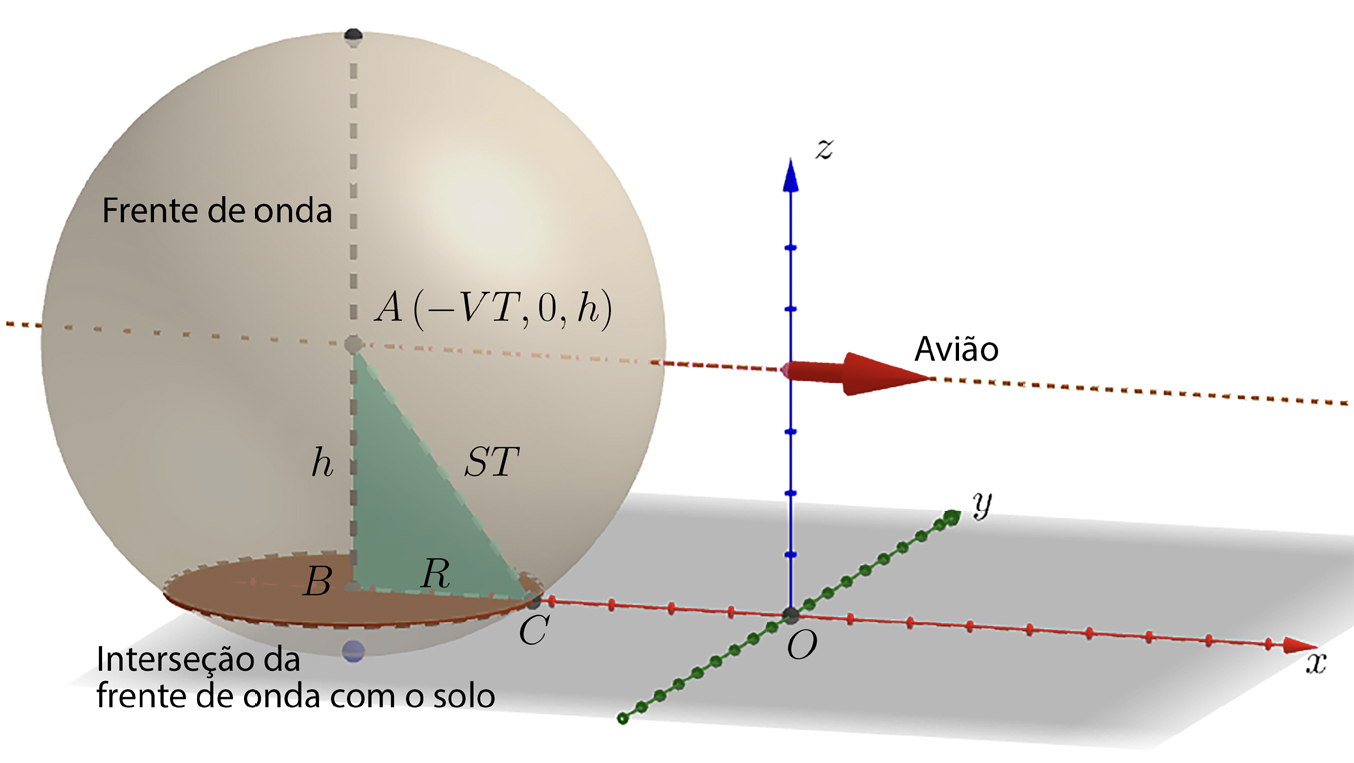
Analisar a zona de audibilidade num certo instante. Por outras palavras, fixamos um instante, digamos, o instante \(0\) (congelamos o tempo nesse instante), onde o avião está no ponto \((0, 0, h)\), e vemos como é a região do solo onde o avião foi ouvido (FIGURA 1).

Dados do problema:

• A altura \(h > 0\) do voo (suposta constante), medida em km.
• A velocidade \(V\) do avião (suposta constante), medida em km/h.
• A velocidade \(S\) de propagação do som (suposta também constante), medida em km/h.
• O avião desloca-se em movimento retilíneo uniforme, ao longo da reta paralela ao eixo dos \(x\)’s, no plano \(Oxz\), a uma altura \(h\) do plano do solo — o plano \(Oxy\). O avião voa da esquerda para a direita, no sentido positivo do eixo dos \(x\)’s. Supomos ainda que o voo é supersónico: \(V > S\).

Cálculos

Analisemos então a zona de audibilidade no instante \(0\). Neste instante o avião está no ponto \((0, 0, h)\), por cima da origem das coordenadas, \(O\). \(T > 0\) horas mais cedo o avião estava no ponto \(A = (−V T, 0, h)\) (FIGURA 1). No ponto \(A\), o motor do avião emitiu um som que se prapaga em todas as direções com velocidade \(S <\)\( V\). A frente de onda tem pois a forma de uma esfera cujo raio cresce com velocidade \(S\).

Qual o raio dessa esfera no instante \(0\)?

Como passaram \(T\) horas, até o avião chegar ao ponto \((0, 0, h)\), é claro que esse raio é igual a \(ST\). Essa esfera, no instante \(t = 0\), interseta o solo segundo uma circunferência centrada em \((−V T, 0, 0)\), e cujo raio é \((R=\sqrt{\left ( ST \right )^{2}-h^{2}}\)), como se deduz facilmente, aplicando o teorema de Pitágoras ao triângulo retângulo \(ABC\), e atendendo a que \(\overline{AB}=h\) e \(\overline{AC}=ST\) (FIGURA 1).

Generalização

O mesmo acontece em cada instante \(T:0<\)\(t\leq T\) — nesse instante o avião está no ponto \((−V t, 0, h)\) e, nesse ponto, o motor do avião emite um som que se prapaga em todas as direções com velocidade \(S\). A frente de onda correspondente tem mais uma vez a forma de uma esfera cujo raio cresce com velocidade \(S <\)\( V\). Essa esfera, no instante \(t = 0\), tem um raio igual a \(St\) e interseta o plano do solo segundo uma circunferência \(Ct\), centrada em \((−V t, 0, 0)\) e cujo raio é \(\sqrt{\left ( St \right )^{2}-h^{2}}\).

No plano \(Oxy\), a equação dessa circunferência é

\(C_{t}:\left ( x+Vt \right )^{2}+y^{2}=\left ( St \right )^{2}-h^{2}\) (1)

Zona de audibilidade

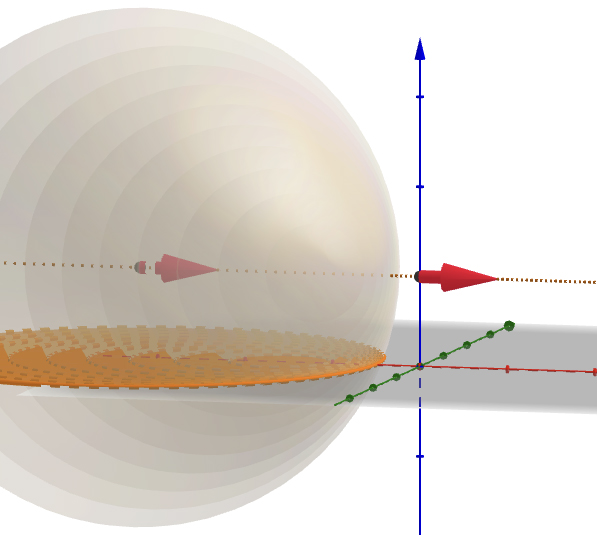
É agora claro que a zona de audibilidade, no instante \(0\) é constituída por todos os pontos do solo que estão dentro dos círculos delimitados por todas estas circunferências \((C_{t}\)), para \(t:0<\)\(t\leq T\) (FIGURA 2), isto é, por todos os pontos \((x, y)\) do solo, que satisfazem as inequações (uma para cada \(t\)):

\(\left ( x+Vt \right )^{2}+y^{2}\leq \left ( St \right )^{2}-h^{2},\; \; \; \forall t:0\leq t\leq T\) (2)

ou, fazendo as contas:

\(\left ( V^{2}-S^{2} \right )t^{2}+2Vxt+\left ( x^{2}+y^{2}+h^{2} \right )\leq 0\; \; \; \forall t:0\leq t\leq T\) (3)

Para cada \(t\), esta é uma inequação do segundo grau em \(t\). Quais as condições em que admite solução? A resposta está dada no teorema seguinte, cuja demonstração é simples:

Teorema

Considere um polinómio quadrático da forma:

\(at^{2}+bt+c\)

com coeficientes \(a > 0\) e \(c > 0\). Para que exista um \(t\geq 0\) que satisfaça a inequação:

\(at^{2}+bt+c\leq 0\)

é necessário e suficiente que:

1. \(b<\)\(0\)
2. \(b^{2}-4ac\geq 0\)

No nosso caso, a inequação é (3) com:

\(a=V^{2}-S^{2}>0,\; \; \; b=2Vx\) e \(c=x^{2}+y^{2}+h^{2}>0\)

Aplicando os critérios do teorema, concluímos que:

1. \(b=2Vx<\)\(0\; \; \; \; \; \Leftrightarrow \; \; \; \; \; x<\)\(0\)
2. \(b^{2}-4ac\geq 0\; \; \; \; \; \Leftrightarrow \; \; \; \; \; \left ( 2Vx \right )^{2}-4\left ( V^{2}-S^{2} \right )\left ( x^{2}+y^{2}+h^{2} \right )\geq 0\)

Esta última desigualdade pode ser escrita na forma:

\(\frac{x^{2}}{\left [ \left ( V^{2}-S^{2} \right )/S^{2} \right ]}-\frac{y^{2}}{h^{2}}\geq 1\)

ou, fazendo \(k=\frac{V}{S}h\), na forma:

\(\frac{x^{2}}{k^{2}-h^{2}}-\frac{y^{2}}{h^{2}}\geq 1\) (4)

Conclusões

1. A zona de audibilidade no instante \(t = 0\) consiste de todos os pontos \((x, y)\) do solo, que satisfazem:



\(\frac{x^{2}}{h^{2}-h^{2}}-\frac{y^{2}}{h^{2}}\geq 1\) e \(x<\)\(0\) (5)



2. A hipérbole de equação:



\(\frac{x^{2}}{k^{2}-h^{2}}-\frac{y^{2}}{h^{2}}=1\) (6)

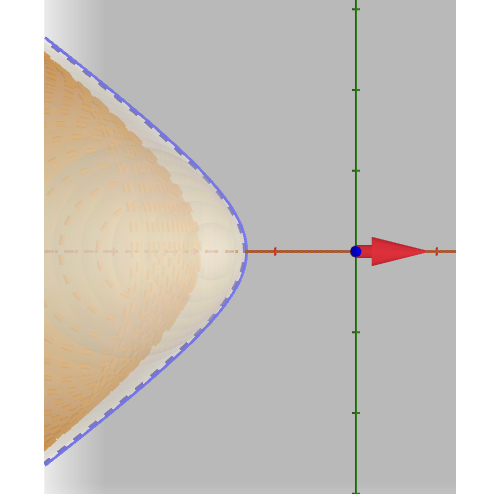
é a envolvente das circunferências \(C_{t}\), dadas por (1) (FIGURA 3).