Motivação

Como aproximar $e^{0,1}$?

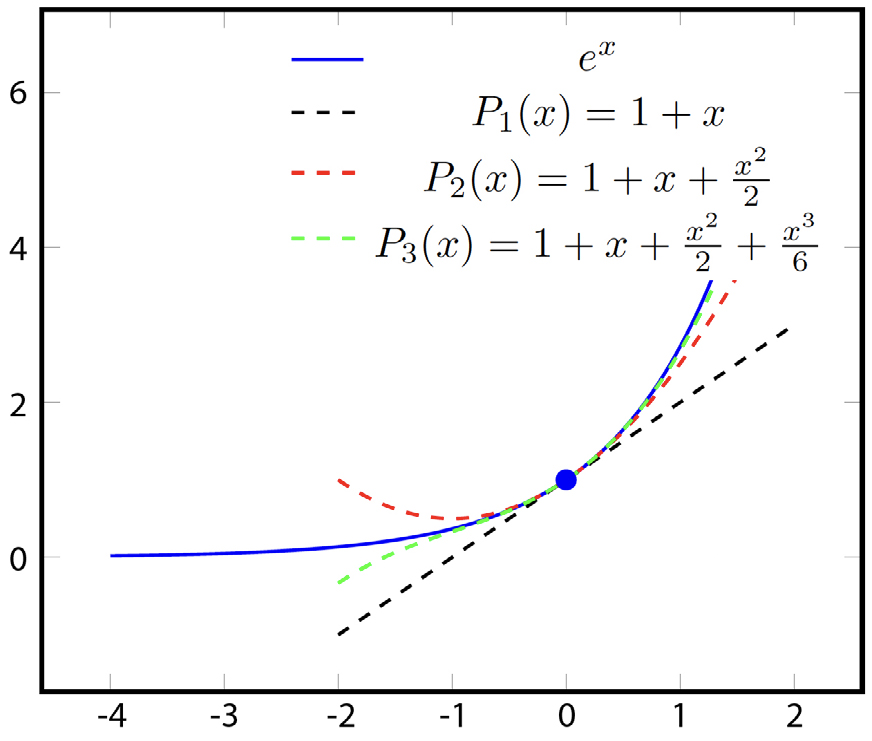
Considere-se $f (x) = e^x$ uma função infinitamente derivável em $0$. Ora, sabe-se que $f (0) = e^0 = 1$. Como a derivada da função exponencial é a própria função exponencial, então $f′ (0) = e^0 = 1$. Sabendo a imagem de $f$ e da sua derivada na origem, pode- se construir a reta tangente a $f$ em $0: y = f (0) + f′ (0) x = 1 + x$. Para pontos $x$ próximos da origem, a reta tangente permite-nos obter uma boa aproximação para $f (x)$. Ou seja, $e^{0,1}\approx e^{0}+e^{0}\times 0,1=1,1$. Ora o valor fornecido pelo computador é: $1,105170918075648$, pelo que se tem uma casa decimal correta.

Como melhorar? Bem, se no caso anterior se construir a reta tangente, polinómio de grau 1, $P_1 (x)$, tal que $f (0) = P_1 (0)$ e $f′ (0) = P′1 (0)$, então pode-se tentar construir um polinómio de grau 2 na condição de adicionalmente satisfazer $f"\left ( 0 \right )=P_{2}^{"}\left ( 0 \right )$. Assim, sendo $P_2 (x) = a + bx + cx^2$, tem-se que $P_2\left ( 0 \right )=a,P_{2}^{'}\left ( 0 \right )=b$ e $P_{2}^{"}\left ( 0 \right )=2c$. Pelo que $a = e^0 = 1$, $b = e^0 = 1$ e $2c = e^0 = 1$, donde o polinómio de segundo grau que verifica as três condições anteriores é $P_2\left ( x \right )=1+x+\frac{1}{2}x^{2}$. Pode-se então aproximar “melhor” $e^{0,1}$ através de $P_2 (0,1) = 1+0,1 + 0, 005 = 1, 105$, e passa-se a ter três casas decimais coincidentes.

Este processo pode ser continuado para um polinómio de grau $n$ centrado em $0$, $0$, $0,P_n\left ( x \right )=1+x+\frac{1}{2}x^{2}+\frac{1}{3}x^{3}+\cdots+\frac{1}{n!}x^{n}$, que se designa por polinómio de Taylor de grau $n$ centrado em 0 (FIGURA 1).

Série de Taylor

Seja $f (x)$ uma função infinitamente derivável. O polinómio de Taylor de grau $n$ centrado em $x_0\in \mathbb{R}$ vem dado por

$P_n\left ( x \right )=\sum_{k=0}^{n}\frac{f^{\left ( k \right )}\left ( x_0 \right )}{k!}\left ( x-x_o \right )^{k}$

sendo $f^{\left ( k \right )}$ a derivada de ordem $k$ de $f$. Na verdade, o valor de $n$ pode crescer até ao infinito (e mais além...). Define-se série de Taylor da função $f$ centrada em $x_0$ e avaliada em $x$ à soma infinita

$f\left ( x \right )=\sum_{k=0}^{\infty }\frac{f^{\left ( k \right )}\left ( x_0 \right )}{k!}\left ( x-x_0 \right )^{k}$.

Para a função exponencial, tem-se

$e^{x}=\sum_{k=0}^{\infty }\frac{e^{x_{0}}}{k!}\left ( x-x_0 \right )^{k}$.

Quando a série se desenvolve em torno de $x_0 = 0$ é designada por série de Maclaurin. A aproximação pelo polinómio de Taylor resulta então de truncar a série de Taylor num número finito de termos.

Várias questões se podem levantar:

• Para aproximar o valor de uma função num ponto, qual o valor de $x_0$ a escolher? A função pode estar definida para todo o real, mas apenas na vizinhança de $x_0$ a aproximação polinomial deve dar bons resultados. Como melhorar a aproximação?
• Que condições devem ser verificadas para que a série seja convergente? Na verdade poderá não haver convergência para um dado valor de $x_0$, e polinómios com elevado grau trazem problemas ao cálculo numérico: crescimento rápido de $n!$ (fração a convergir para zero muito rapidamente) e potências muito elevadas de $\left ( x-x_0 \right )^{k}$.

Para melhorar o cálculo numérico pode-se evitar o cálculo explícito das potências e fatorial, basta verificar (método de Horner) que

$e^{x}=1+x(1+\frac{x}{2}(1+\frac{x}{3}(1+\cdots$

pode ser usado para exprimir a série de Taylor da função exponencial em torno de $0$.

Análise do erro

Sendo $P_n (x)$ o polinómio de Taylor de grau $n$ centrado em $x_0$, pode-se definir o erro absoluto em aproximar $f (x)$ por $P_n (x)$:

$R_n\left ( x \right )=\left | f\left ( x \right )-P_n\left ( x \right ) \right |$.

No caso da função exponencial

$R_n\left ( x \right )=\left | \frac{e^{\left ( n+1 \right )c}}{\left ( n+1 \right )!}\left ( x-x_0 \right )^{n+1} \right |$

$=\left | e^{c}\frac{e^{\left ( n+1 \right )}}{\left ( n+1 \right )!}\left ( x-x_0 \right )^{n+1} \right |$

sendo $c$ um valor real que satisfaz $x_0 \leq c \leq x$. Ora como a função exponencial é crescente, então atinge o maior valor no extremo direito do intervalo $[x_0, x]$. Então, o erro absoluto é majorado por

$R_n\left ( x \right )\leq \left | e^{x}\frac{\left ( x-x_0 \right )^{n+1}}{\left ( n+1 \right )!} \right |$

e o relativo por

$\frac{R_n\left ( x \right )}{e^{x}}\leq \left | \frac{\left ( x-x_0 \right )^{n+1}}{\left ( n+1 \right )!} \right |$.

Note-se que $\left | P_{n+1}\left ( x \right )-P_n\left ( x \right ) \right |=\left | \frac{\left ( x-x_0 \right )^{n+1}}{\left ( n+1 \right )!} \right |$, e o erro relativo em $P_n (x)$ é majorado pelo termo de ordem $n + 1$ da série de Taylor. Assim, pode-se determinar quantos termos $n$ terão de ser considerados para que uma precisão de $\textrm{tol}$ seja verificada: $\left | \frac{\left ( x-x_0 \right )^{n}}{n!} \right |\leq \textrm{tol}$.

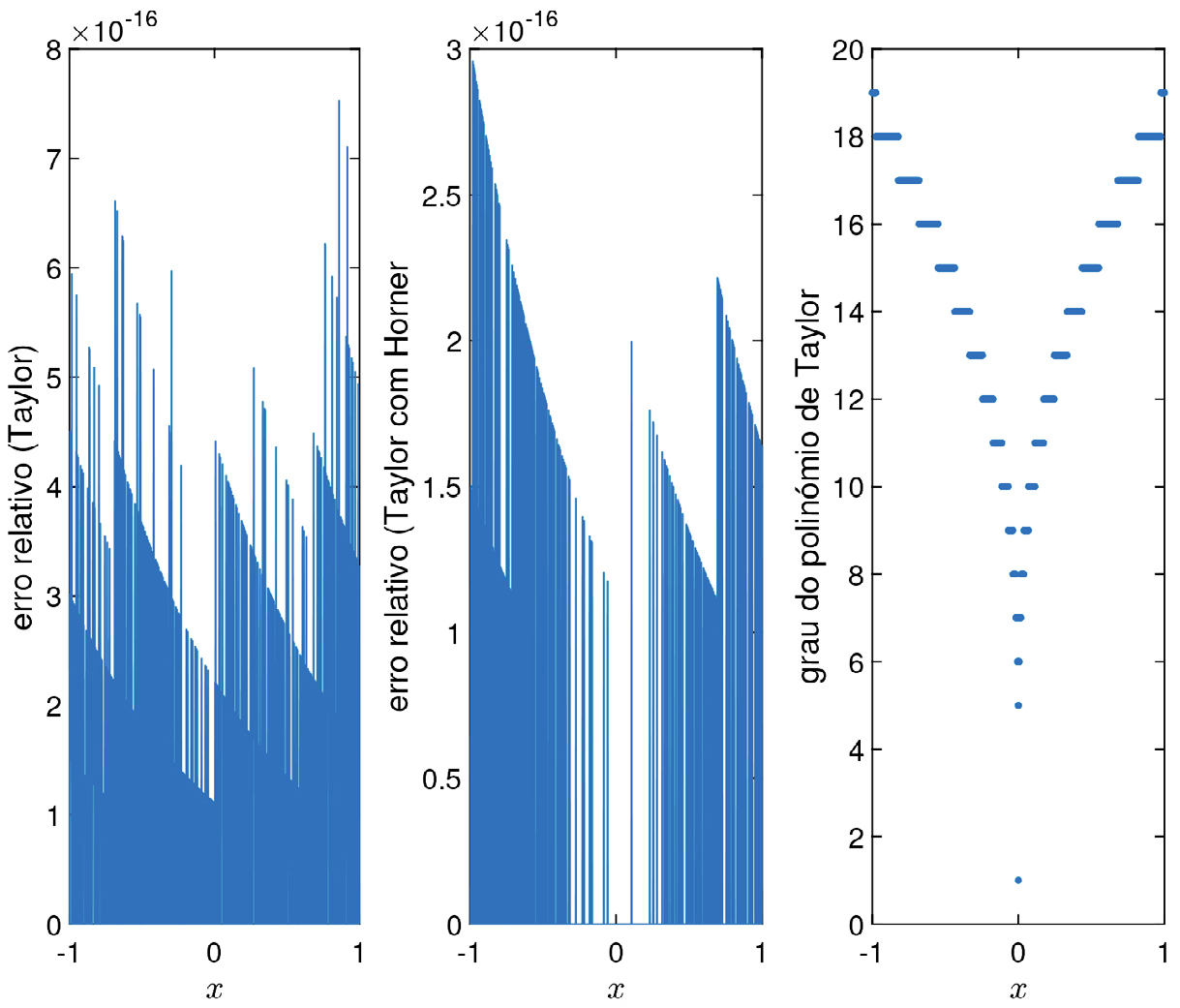
Na FIGURA 2 mostram-se os erros relativos ao aproximar $e^{x}$, para $x\in \left [ -1,1 \right ]$, usando polinómios de Taylor de grau $n$, centrados em $0$, a satisfazer $\left | \frac{x^{n}}{n!} \right |\leq 10^{-16}$. À medida que o valor que se pretende aproximar se afasta de $0$, o grau do polinómio a usar vai aumentando, mas a qualidade da aproximação vai sendo menos boa. Isso é cada vez mais evidente quanto maior for a amplitude de valores a considerar para $x$ (FIGURA 3).

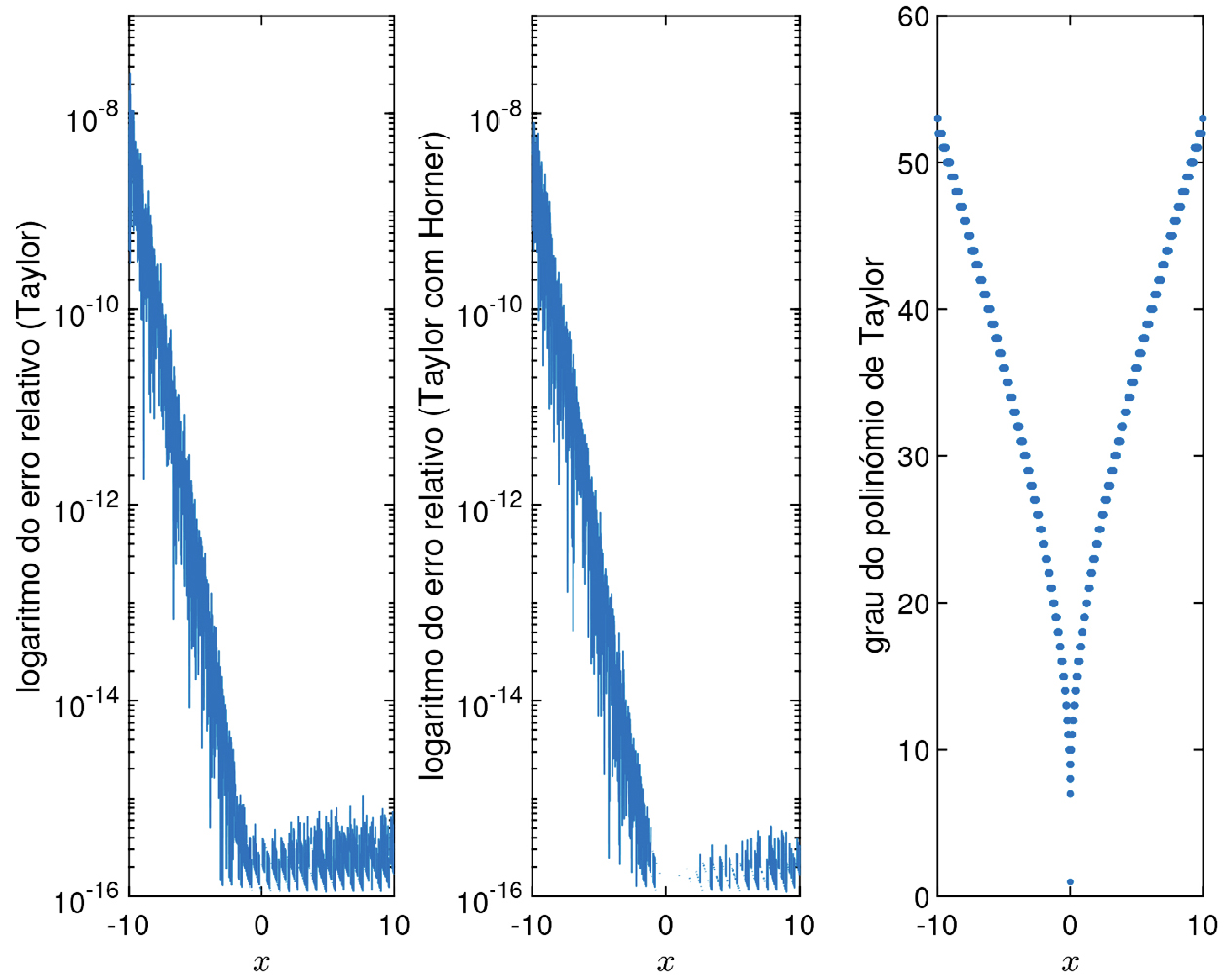
Redução da distância do argumento de aproximação

Pode-se recorrer a propriedades das funções para focar a aproximação e assim evitar usar grau polinomial elevado e com perda de qualidade de aproximação.

No caso da função exponencial sabe-se que $P_n\left ( x \right )=\sum_{k=0}^{n}\frac{x^{k}}{k!}$ pode ser uma boa aproximação de $ex$ desde que $x$ seja próximo de $0$. Então uma ideia seria a de “trazer” a aproximação de $e^x$ para “perto” de $e^0$. Ora se se considerar $x=l\textrm{In}2+r$ para um inteiro positivo $l$ e um real $r$ com $\left | r \right |\leq \frac{1}{2}\textrm{In}2$ (valor suficientemente próximo de zero) então, $e^{x}=e^{l\textrm{In}2+r}=2^{l}e^{r}$.

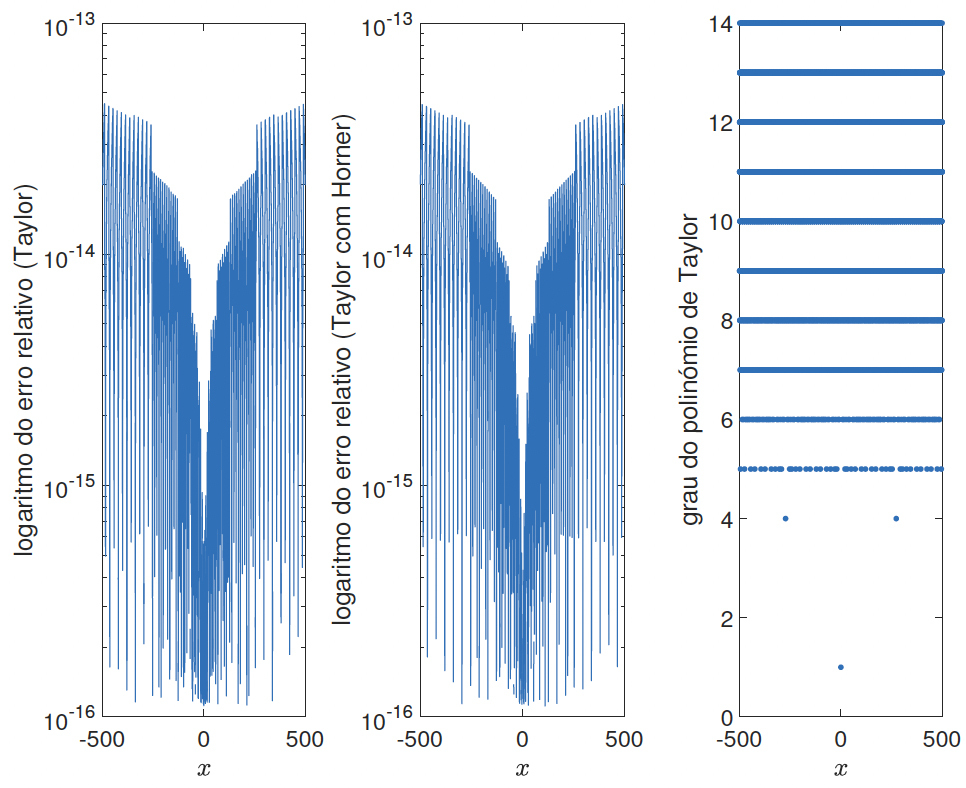
Resulta imediato que se pode aproximar $e^x$ à custa da aproximação de Maclaurin da exponencial em $r$ e de $2(l)$ que é fácil e eficiente de calcular. Para que l seja inteiro e $\left | r \right |\leq \frac{x^{n}}{n!}$, de $l=\frac{x}{\textrm{In}2}-\frac{r}{\textrm{In}2}$ pode-se impor que $l=\left \lceil \frac{x}{\textrm{In}2}-\frac{1}{2} \right \rceil$ (arredondamento para cima). Sabendo $l$ e $x$ calcula-se $r$ e usa-se $2^lP_n (r)$ para aproximar $e^x = 2^le^r$. Da FIGURA 4 ilustra-se que, o erro relativo (em escala logarítmica) é muito bom mesmo para valores distantes de $0$ sendo que, o grau polinomial usado foi no máximo de 14.

As aproximações são já muito boas: note-se que para aproximar $e^{500}\approx 1, 03610^{217}$ se está a cometer um erro relativo de $2\times 10^{-14}$ (i.e., erro na décima quarta casa decimal de um número imensamente grande).

Pode-se fazer ainda melhor recorrendo a abordagens mais sofisticadas e eficientes de efetuar a redução da distância do argumento de aproximação, mas sobretudo, considerando outras aproximações, como interpolação polinomial. Estas matérias de teoria de aproximação e de implementação em computador são abordadas em análise numérica e matemática computacional.

O número de Euler

Antes de terminar vai-se destacar que a aritmética efetuada num computador é em precisão finita. Num computador os números racionais têm de ser armazenados num espaço que é finito, em oposição à sua infinitude. Os computadores trabalham numa base 2, resultando daí que muitos números racionais não têm representação exata. Por exemplo, a fração decimal $0,1$ não tem representação exata em base 2 mas tem em base 10 $\left ( 0,1=1\times 10^{-1} \right )$.

A representação de números reais em computador segue, desde 1985, a norma IEEE-754 na utilização da aritmética binária para números de vírgula flutuante, relativo ao armazenamento, métodos de arredondamento, ocorrência de underflow/overflow e realização das operações aritméticas básicas. Um sistema de vírgula flutuante permite representar, com um número fixo de dígitos, números racionais com diferentes ordens de magnitude. A representação finita em base 2 usa 3 componentes: o sinal, o expoente e a mantissa: $\left [ \pm \right ]\left [ \textrm{mantissa} \right ]\times 2^{\left [ \textrm{expoente} \right ]}$. O sistema a 64-bits (dupla precisão) usa 1 bit para o sinal, 11 para o expoente e 52 para a mantissa (sendo de 8 bits para o expoente e de 23 bits para a mantissa em precisão simples). O real $0,1$ tem a seguinte representação binária em 64- bits: sinal $(0)$, expoente ($01111111011$) e mantissa 1001100110011001100110011001100110011001100110011010), a que corresponde, de volta à base 10, a melhor representação possível de

$0.100000000000000005551115123126$.

É curioso testar no vosso computador que $0,1 + 0, 2 − 0,3 = 5, 5511 \times 10^{-17}$ e não $0$. Na verdade para o computador tal resultado deve ser considerado 0, pois o cálculo em precisão dupla fornece uma precisão relativa de cerca de 16 dígitos decimais.

A precisão de computador pode ser calculada através do épsilon de máquina: o menor número que separa 1 do próximo número representável (2, 2204 \times 10^{-16}). O épsilon de um número maior é também maior: o de $100000$ é $1, 4552 \times 10^{-11}$. Assim se efetuarem no vosso computador ou numa calculadora o seguinte cálculo $10^{12}-10^{12}+10^{-5}$ o resultado será o esperado $10^{-5}$, pois ao subtrair dois números com a mesma representação e adicionarem um terceiro, resulta o terceiro. Mas, a propriedade associativa não existe em vírgula flutuante: o cálculo de $10^{12}-10^{-5}+10^{12}$ vale $0$. Note-se que o épsilon de $10^{12}$ é $1,2207 \times 10^{-4}$ e portanto $10^{12}+10^{-5}=10^{12}$. O próximo número representável após $10^{12}$ é $10^{12}+1,2207\times 10^{-4}$. Por este facto, os números reais em computador não são uniformemente espaçados. No standard IEEE 754, existe maior representatividade próximo de 0 do que para valores muito grandes em valor absoluto.

Sabe-se que e é irracional e que pode ser aproximado por $\lim_{n\rightarrow \infty }\left ( 1+\frac{1}{n} \right )^{n}$ e que portanto este limite corresponde à soma da série de Taylor da função exponencial em torno de $1:e=\sum_{k=0}^{\infty }\frac{1}{k!}$.

A TABELA 1 mostra as aproximações calculadas para e via polinómios de Taylor e através de $\left ( 1+\frac{1}{n} \right )^{n}$, para valores crescentes de n. Ora com um polinómio de Taylor centrado na origem de grau 19 obtém-se quase a precisão máquina, sendo que para graus maiores não há melhoria na aproximação. Já para o cálculo via a expressão do limite, com $n = 100000$ tem-se ainda um erro na sexta casa decimal. Poder-se-ia pensar que o erro relativo baixaria consistentemente para valores crescentes de $n$. Tal não é o caso atendendo aos erros numéricos, que não vão permitir melhorar a aproximação de e com a expressão $\left ( 1+\frac{1}{n} \right )^{n}$

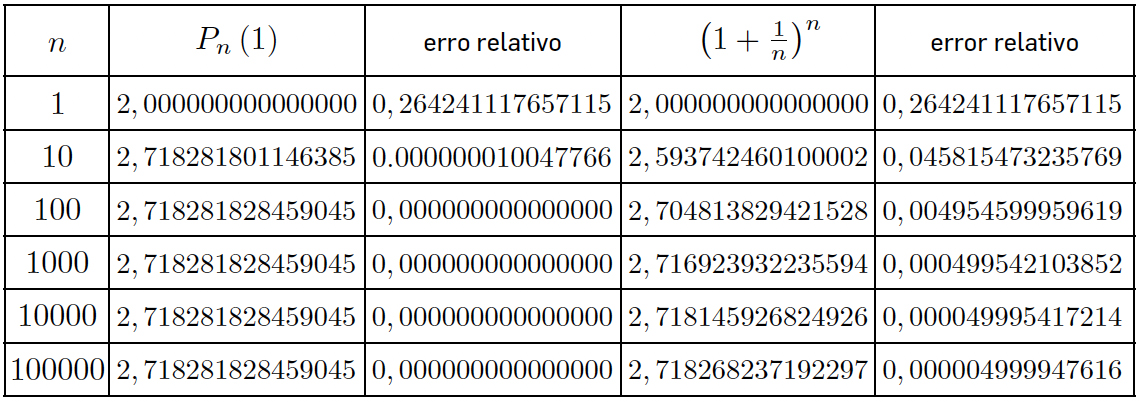
Por exemplo, para $n = 10^{15}$ a aproximação calculada é... $3, 03503520654926!$ (com erro relativo $0,116527055720995$).