Envolventes
📧
- CMUP/ Universidade do Porto
Referência Tavares, J., (2022) Envolventes, Rev. Ciência Elem., V10(1):007
DOI http://doi.org/10.24927/rce2022.007
Palavras-chave Espaço, equação de posição, retas, funções, curvas, planos, referencial cartesiano, ponto característico
Resumo
Neste curto artigo vamos explorar um processo dinâmico de produzir superfícies regradas planas, a partir do movimento de retas num plano, que geram, por sua vez, curvas especiais, como envolventes, evolutas e outras, sob certas condições técnicas que não são especificadas, para manter o artigo num nível elementar. A generalização natural consiste em gerar superfícies regradas no espaço, usadas, por exemplo, em obras arquitetónicas de Calatrava e outros.
Um modelo
Os padrões que vamos analisar neste artigo têm todos uma característica comum: são formados pelas diversas posições de uma reta \(R\) que se desloca no plano, com um movimento que depende de uma variável \(t\) (tempo), que varia num certo intervalo \(T\). Por outras palavras, em cada instante \(t\in T\), a reta \(R\) ocupa uma posição que designamos por \(R(t)\), e o padrão é formado por todas essas retas \(\left \{ R\left ( t \right ) \right \}_{t\in T}\).
Como se sabe, a equação de uma reta no plano, quando neste se fixa um referencial cartesiano, é da forma:
\(ax+by+c=0\)
Como a reta se move com o tempo \(t\), a equação da sua posição no instante \(t\) será pois do tipo:
\(a(t)x+b(t)y+c(t)=0\)
onde \(a (t)\), \(b (t)\) e \(c (t)\) são funções de \(t\), bem determinadas pela lei do movimento de \(R\) (vamos supôr que \(R(0) = R\)). Vejamos um exemplo concreto.
Um exemplo concreto
\(R\left ( t \right ):\; \; \; \; \; \left ( 1-2t \right )x+y+2t\left ( t-1 \right )=0\)
Aqui as funções \(a\), \(b\) e \(c\) são respetivamente, \(a (t) = 1 − 2t\), \(b (t) \equiv 1\) e \(c (t) = 2t (t − 1)\). Suponhamos ainda que t varia no intervalo \(T = [−5, 5]\). O padrão é o seguinte (veja o applet Geogebra na versão online):
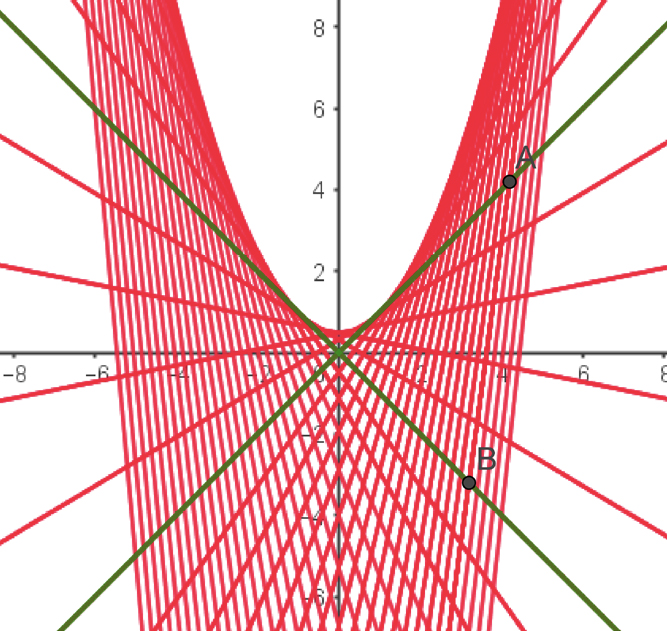
Neste exemplo as retas \(\left \{ R\left ( t \right ) \right \}_{t}\) parecem envolver uma parábola. O exemplo foi construído da seguinte maneira: considerámos as duas retas \(y = x\) e \(y = −x\) (as bissetrizes dos quadrantes) no plano. Sobre a reta \(y = x\), desloca-se um ponto \(A\), para cima, com velocidade uniforme, partindo do ponto \((−5,−5)\), no instante \(t = −5\). No instante \(t\geq -5\), o ponto \(A\) estará na posição \(A(t) = (t, t)\). Sobre a reta \(y = −x\) desloca-se, para baixo, um outro ponto \(B\), com a mesma velocidade uniforme, partindo do ponto \((−6, 6)\), no instante \(t = −5\). O ponto \(B\) no instante \(t\geq -5\) estará na posição \(B (t) = (−1 + t, 1 − t)\).
Para cada \(t\) no intervalo \(T = [−5, 5]\), a reta \(R(t)\) é a que une os pontos \(A(t)\) e \(B (t)\). A sua equação é:
\(\left ( 1-2t \right )x+y+2t\left ( t-1 \right )=0\)
como o leitor poderá verificar sem qualquer dificuldade — exatamente a equação que ilustrámos na secção anterior. Eis algumas questões:
- como podemos mostrar com rigor que as retas \(R(t)\) envolvem uma parábola?
- o que significa envolver?
- como calculamos a equação dessa parábola?
Antes de responder a estas e outras questões, vamos analisar mais alguns exemplos.
Mais exemplos
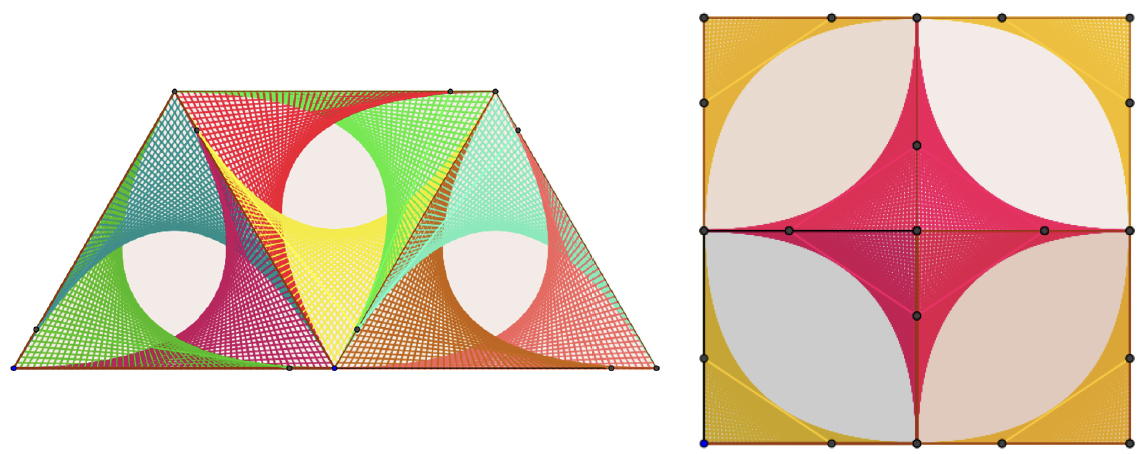
Os exemplos seguintes são obtidos juntando vários módulos idênticos ao descrito na secção anterior. Assim, na FIGURA 2A), à esquerda (e no applet da versão online) temos três módulos, formando um triângulo equilátero, cada um deles envolvendo uma parábola. Já na FIGURA 2B) temos quatro módulos, formando um quadrado, cada um deles envolvendo uma parábola.
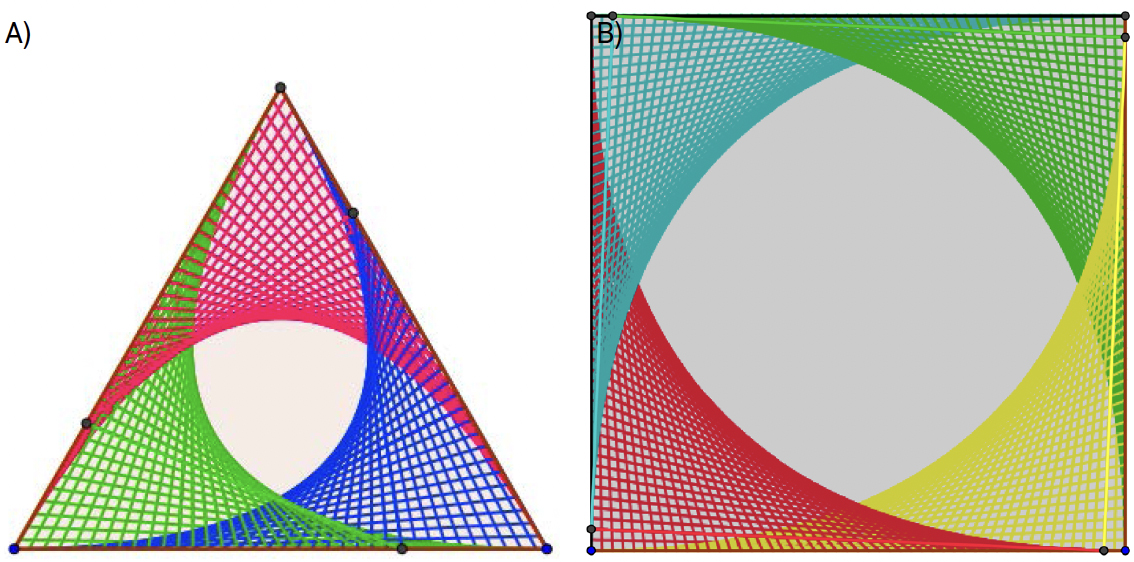
O leitor não terá dificuldade em descrever como são formados nas FIGURAS 2A) e 2B) (ver os applets na versão online). Espera-se que se sinta suficientemente estimulado para construir os seus próprios exemplos com Geogebra, ou qualquer outro programa de Geometria Dinâmica. Mãos à obra, então!
A teoria — Definição de envolvente
Considere de novo uma família de retas \(\left \{ T\left ( t \right ) \right \}_{t}\), que continuamos a imaginar como as sucessivas posições resultantes de um determinado movimento de uma reta dada \(R\). A envolvente da família de retas \(\left \{ T\left ( t \right ) \right \}_{t\in T}\) é uma curva \(E\) que, em cada um dos seus pontos, é tangente a alguma das retas \(R(t)\). Para explicar como calculamos a envolvente, vamos de novo usar o exemplo concreto que considerámos no início:
\(R\left ( t \right )\doteq \left ( 1-2t \right )x+y+2t\left ( t-1 \right )=0\)
Ponto característico
Fixemos um instante \(t\) arbitrário e a reta \(R(t)\). Para um \(h > 0\) muito pequeno, consideremos a reta \(R(t + h)\). Qual a equação desta reta? É evidentemente:
\(R(t + h) = (1 − 2 (t + h)) x + y +2 (t + h) ((t + h) − 1) = 0\)
Estas duas retas intersetam-se num ponto situado na reta \(R(t)\). O problema é determinar (com \(t\) fixo), a posição limite deste ponto, quando \(h\rightarrow 0\). A este ponto limite chama-se o ponto característico \(C (t)\) da reta \(R(t)\) (FIGURA 4).
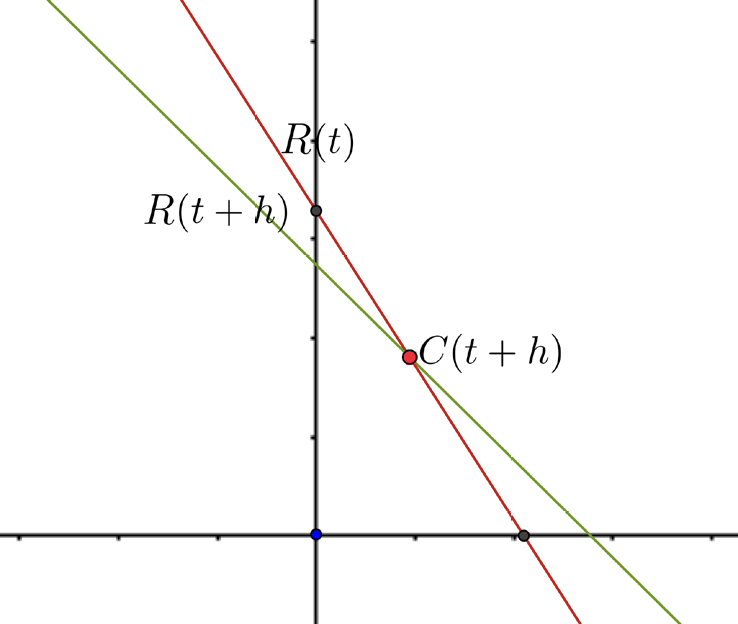
Envolvente
Quando \(t\) varia, o ponto característico \(C (t)\) descreve uma curva que é exatamente a envolvente das retas \(R(t)\). No exemplo que temos vindo a tratar, será uma parábola.
Vejamos então como calcular a equação da envolvente. Para um \(t\) fixo e um \(h\) muito pequeno, mas diferente de \(0\), o ponto de interseção das duas retas próximas \(R(t)\) e \(R(t + h)\), calcula-se procurando a solução \((x, y)\) das duas equações seguintes:
\(\left\{\begin{matrix} R\left ( t \right ) & = & \left ( 1-2t \right )+x+y+2t\left ( t-1 \right ) & = & 0\\ R\left ( t+h \right ) & = & \left ( 1-2\left ( t+h \right )\right )x+y+2\left ( t+h \right )\left (\left ( t+h \right )-1 \right ) & = & 0 \end{matrix}\right.\)
Mas não podemos fazer \(h = 0\) nestas equações — senão elas coincidiam e haveria uma infinidade de soluções. Em vez disso, substituímos o sistema anterior pelo equivalente (não esqueça que \(h\neq 0\)):
\(\left\{\begin{matrix} R\left ( t \right ) & = & 0\\ \frac{R\left ( t+h \right )-R\left ( t \right )}{h} & = & 0 \end{matrix}\right.\)
Fazemos agora \(h\rightarrow 0\) na segunda equação, com \(t\) fixo, e representamos o resultado por \(\partial _{t}R\left ( t \right )\):
\(\lim_{h\rightarrow 0}\frac{R\left ( t+h \right )-R\left ( t \right )}{h}=\partial _{t}R\left ( t \right )\)
A equação da envolvente calcula-se finalmente, eliminando t nas duas equações seguintes:
\(\left\{\begin{matrix} R\left ( t \right ) & = & 0\\ \partial _tR\left ( t \right ) & = & 0 \end{matrix}\right.\)
que são, no nosso exemplo concreto:
\(\left\{\begin{matrix} \left ( 1-2t \right )x+y+2t\left ( t-1 \right ) & = & 0\\ -2x+2\left ( t-1 \right )+2t & = & 0 \end{matrix}\right.\)
A segunda equação dá \(t = (1 + x) /2\), valor que substituímos na primeira, para obter a equação da envolvente:
\(y=\frac{1+x^{2}}{2}\)
Exemplo de Steiner
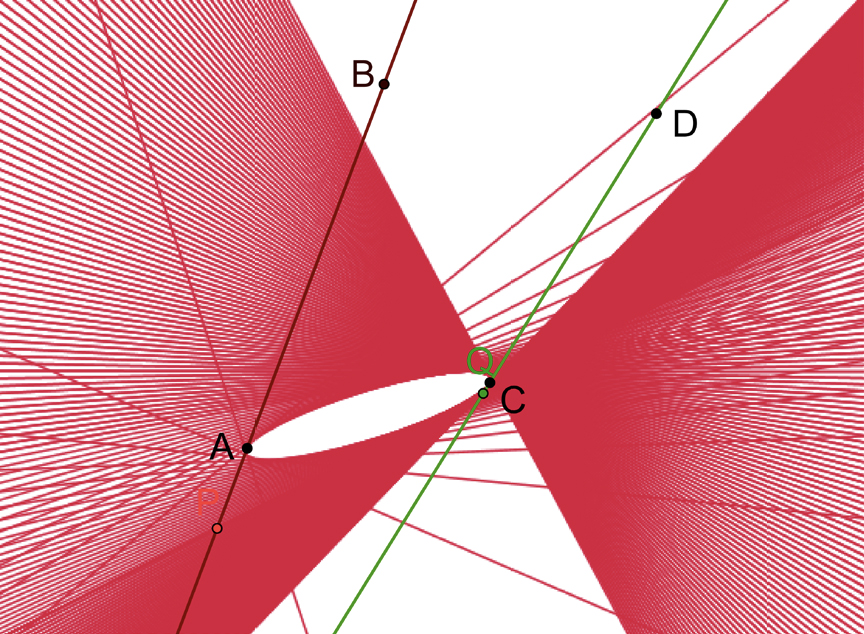
Consideremos duas retas — uma definida por dois pontos \(A\) e \(B\), e outra definida por dois pontos \(C\) e \(D\). Para cada \(t\) definimos dois pontos:
\(P(t)=A+t\frac{\overrightarrow{AB}}{\left \| \overrightarrow{AB} \right \|}\) na reta \(AB\), e \(Q(t)=C+\frac{1}{t}\frac{\overrightarrow{CD}}{\left \| \overrightarrow{CD} \right \|}\) na reta \(CD\)
e ainda a reta \(R(t)\) definida pelos dois pontos \(P (t)\) e \(Q(t)\). É possível provar que a envolvente dessas retas é uma elipse (FIGURA 5 e o applet na versão online):
Evoluta de uma curva plana
Consideremos uma curva \(\alpha (t)\), com \(\alpha'\left ( t \right )\neq0\). Para cada \(t, \alpha (t)\) admite uma reta tangente bem definida e portanto uma reta normal \(N (t)\), também bem definida. Pondo \(\alpha (t) = (x (t) , y (t))\), então a reta normal \(N (t)\) é definida pela condição seguinte:
\(\left ( X-x\left ( t \right ),Y-y(t) \right )\cdot\left ( x'\left ( t \right ),y'\left ( t \right ) \right )=0\)
Aqui \((X, Y )\) representa um ponto genérico sobre a reta \(N (t)\). A equação de \(N (t)\) é pois:
\(x'(t)\left ( X-x(t) \right )+y'\left ( t \right )\left ( Y-y\left ( t \right ) \right )=0\)
A envolvente das retas normais \(N (t)\) chama-se a evoluta da curva \(\alpha\). Na FIGURA 6 (veja os applets na versão online), mostram-se as evolutas de uma elipse e de uma parábola.
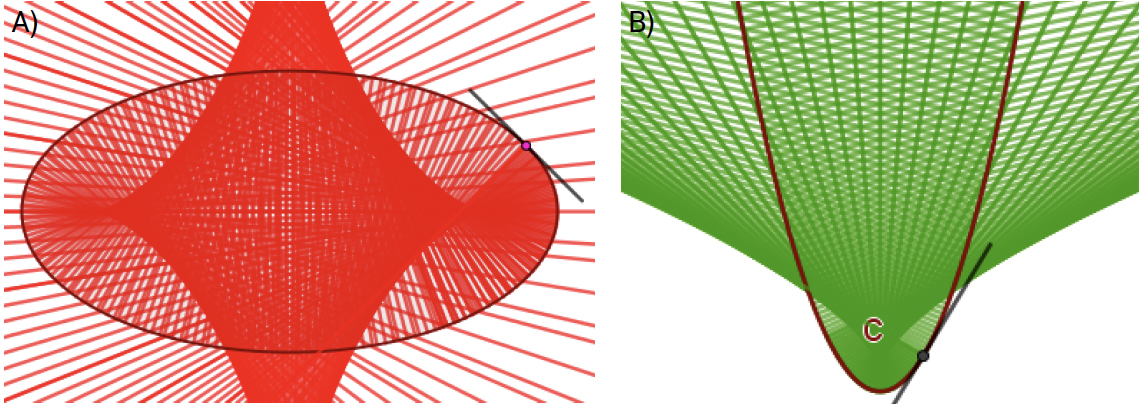
Referências
- 1 PEDIGO, J. et al., Wonderful Curves Sampler Quilt Block Book: 30 Blocks, 14 Projects, Endless Possibilities, Landauer Publishing, ISBN-10: 9781947163720.
- 2 BOLTYANSKY, V., Envelopes. Popular lectures in mathematics, Pergamon Press and MIR Editions. 1964.
- 3 HANNA, G. & JAHNKE, H. N., Arguments from Physics in Mathematical Proofs: An Educational Perspective, For the Learning of Mathematics, 22, 3, pp. 38-45.
Este artigo já foi visualizado 1765 vezes.



