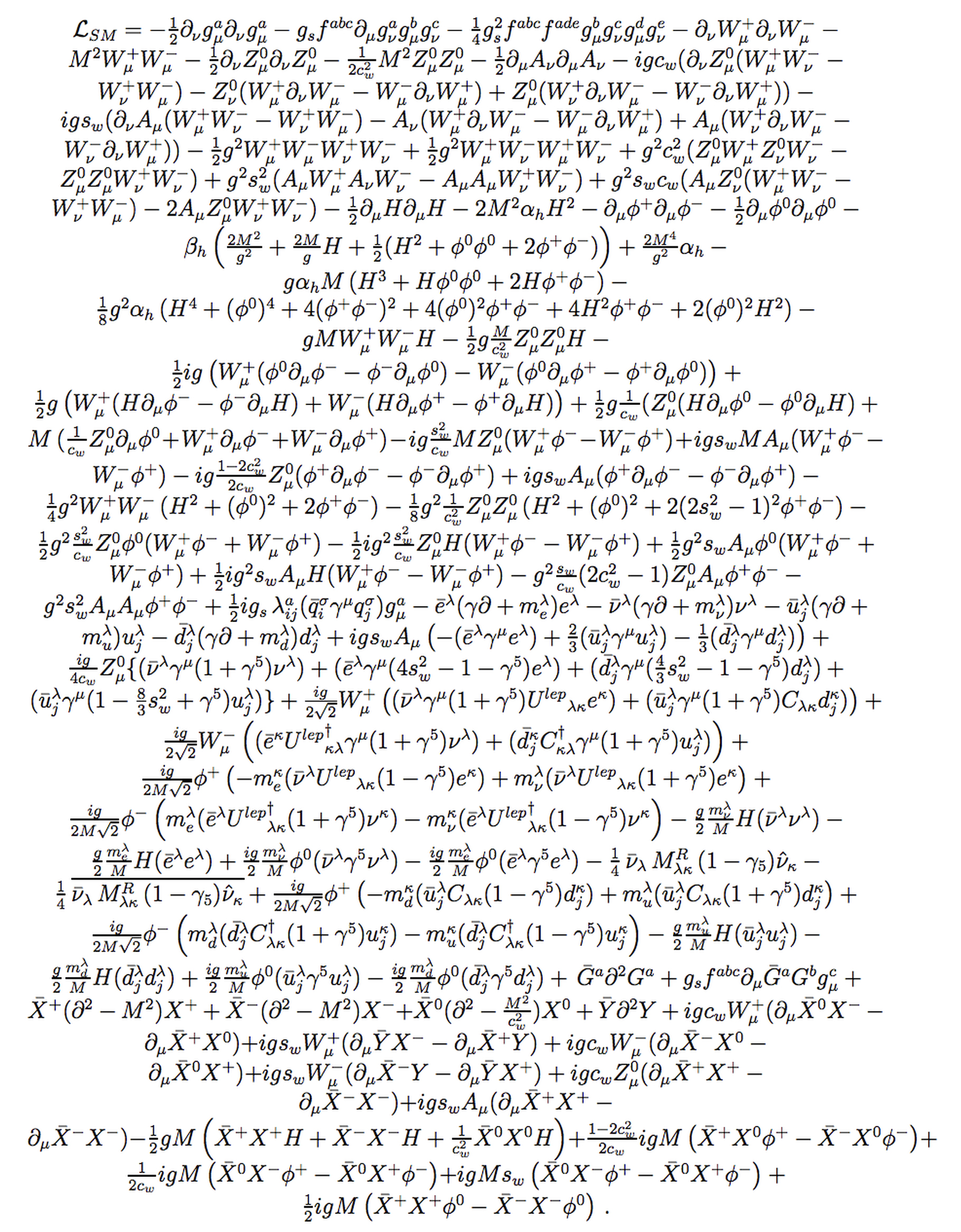
A imagem de destaque deste número da RCE, mostra o Lagrangeano do modelo padrão que incorpora o nosso conhecimento de todos os diferentes tipos de partículas elementares encontradas na natureza.

A evidente complexidade desta fórmula matemática, motivou o grande matemático Alain Connes, Medalha Fields em 1982, a encontrar um modelo alternativo que fosse de interpretação muito mais simples.

A abordagem de Connes (On the fine structure of spacetime), distinta da abordagem tradicional da comunidade da física de partículas, consiste em identificar uma estrutura de espaço-tempo que poderia dar origem ao Modelo Padrão acoplado à gravidade – para alguns a última teoria de tudo!

Esta é uma história fascinante de interação entre matemáticos e físicos, na busca incessante de uma teoria de grande unificação, cuja solução poderá estar em novas e revolucionárias abordagens. Mas o caminho percorrido é já, por ele próprio, uma conquista verdadeiramente extraordinária das capacidades da mente humana.

João Nuno Tavares
DM/ Universidade do Porto

A complexidade da fórmula apresentada, revela uma beleza estética surpreendente.

A Matemática contém uma forma inefável de beleza, refletida nas estruturas que cria e que refletem padrões subtis, de outro modo inacessíveis, que fazem parte da própria textura do universo, assim como na ordem e no rigor com que organiza o conhecimento que vai acumulando. Os matemáticos há muito que comparam a experiência da beleza matemática à da beleza visual e musical.

Uma fórmula matemática é bela. Pode despertar a mesma sensação de beleza que desperta a escrita baseada em alfabetos simbólicos (mandarim, árabe) ou figurativos (egípcio). O neurocientista Semir Zeki sugere que, ao considerar a beleza, os matemáticos podem estabelecer uma conexão profunda entre o cérebro humano e o mundo natural — a experiência da beleza pode ser um indicador da verdade sobre o universo, diz.

Muitos matemáticos dizem que lutam pela beleza da mesma forma que um compositor ou um pintor fariam.

António Machiavelo
DM/ Universidade do Porto