A teoria do Big Bang é o modelo amplamente mais aceite pela comunidade científica para explicar a origem do Universo, tendo várias comprovações observacionais que vão desde a existência de uma radiação cósmica de fundo à previsão da nucleossíntese primordial e abundância relativa de elementos químicos leves. Todavia, existiam outras questões para as quais a teoria anterior não dava uma explicação satisfatória, nomeadamente os problemas do horizonte, da planura, da ausência de defeitos topológicos e da formação de estruturas.

O primeiro problema tem a ver com o seguinte: porque é que as estruturas no Universo parecem praticamente iguais em qualquer lugar e em qualquer direção que se observe, isto é, porque parece o Universo homogéneo e isotrópico? Na realidade, vemos que a temperatura do Universo hoje é sensivelmente a mesma em qualquer par de regiões opostas entre si na radiação cósmica de fundo. Mas isso seria impossível, uma vez que não houve tempo suficiente no passado para que as partículas de luz, os fotões, interagissem entre si num processo de termalização, pois estas só desacoplaram da matéria cerca de 380 mil anos após o Big Bang. Assim, qualquer região separada de outra por 2 graus no Universo seria causalmente desconexa.

O segundo problema tem a ver com a curvatura espacial do Universo ser plana. Assim, parece haver condições iniciais do Universo muito especiais para que ele fosse e/ou se mantivesse espacialmente plano, uma vez que pequenos desvios levariam a cenários bastante diferentes da evolução do Universo: valores acima de uma dada densidade crítica levariam a um Universo muito denso e que colapsaria num Big Crunch; valores abaixo dessa densidade promoveriam um Universo essencialmente vazio onde a gravidade não conseguiria formar as estruturas que observamos no Cosmos.

O terceiro problema do modelo quente do Big Bang diz respeito à ausência de defeitos topológicos observáveis no Universo. Com efeito, a Física do Universo primordial depende muito da Física de Partículas, uma vez que se supõe, na Teoria da Grande Unificação, que em muito altas energias as quatro interações fundamentais se juntam num único grupo de simetria. Em particular, na Física de Partículas existem diversas situações nas quais defeitos topológicos ocorrem, como por exemplo quando ocorre uma transição de fase e correspondente quebra de simetria, algo que seria natural de acontecer com o arrefecimento do Universo à medida que ele se expande. Exemplos destes defeitos são as texturas, parede de domínio, as cordas cósmicas ou os monopólos, que correspondem a defeitos a 3, 2, 1 e 0 dimensões, respetivamente. Em particular, o cálculo do número de monopólos produzidos, por exemplo, na quebra de simetria eletrofraca demonstra que aqueles seriam a forma dominante de energia, algo que não se observa em nenhum local do Universo.

Por seu turno, o quarto problema tem a ver com as inomogeneidades locais do Universo. Isto é, nós observamos galáxias, sistemas planetários, estrelas, entre outros, porque houve possibilidade de colapso gravitacional devido a desvios da homogeneidade a larga escala. Adicionalmente, também se observam grandes vazios, regiões sem matéria, em virtude da atração gravitacional em regiões vizinhas.

A resposta a estes problemas surge com o paradigma inflacionário que implica um período de expansão quase exponencial do espaço-tempo após o Big Bang. Diversos contributos e classes de modelos foram propostos. Em 1979 e 1980, o físico soviético Alexei Starobinsky notou que correções quânticas à teoria da Relatividade Geral deveriam ser importantes no Universo primordial, sendo que tipicamente eram termos quadráticos da curvatura escalar no funcional ação de Einstein-Hilbert. Ora, isto significa que quando as curvaturas são elevadas, tal como no Universo primordial, então os termos quadráticos comportar-se-iam como uma constante cosmológica, descrevendo um estado do Universo muito simétrico designado de Sitter, sendo na realidade substituto da singularidade inicial^{1, 2}. De facto, este modelo de Starobinsky, quando analisado no vazio (sem matéria), corresponde a um modelo particular da classe de teorias alternativas da gravidade proposta para explicar a matéria escura e a energia escura, nomeadamente as chamadas teorias f(R).

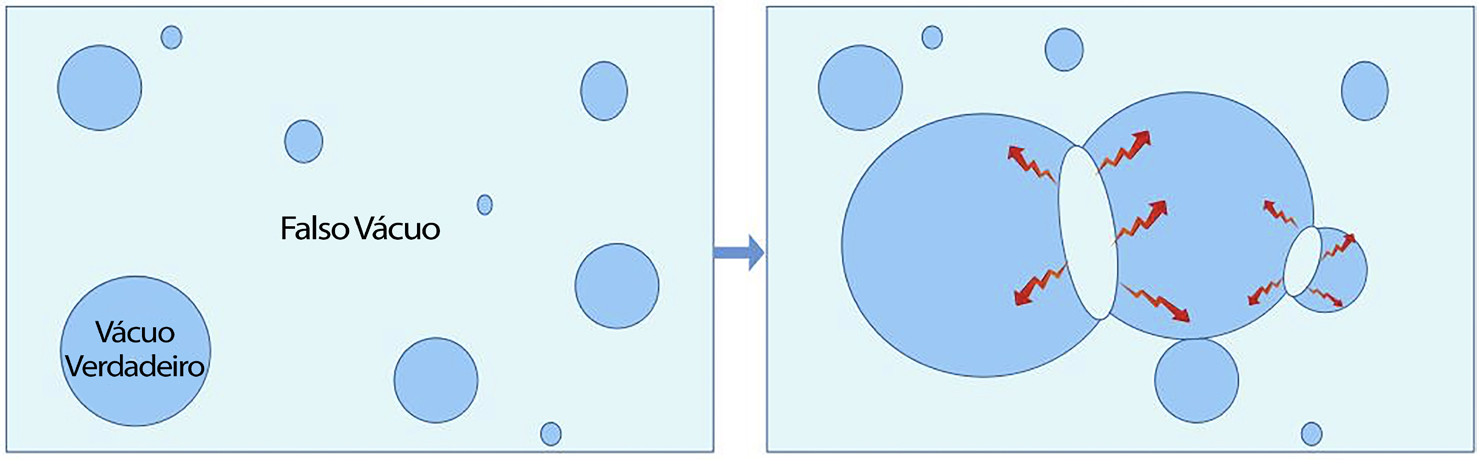
Simultaneamente, e de forma independente, o físico norte-americano Alan Guth publicou um estudo, em 1981, enquanto investigava o problema da não observação de monópolos magnéticos no Universo, em que mostrou que existindo um estado metaestável de falso vácuo de energia positiva, que funcionaria como uma constante cosmológica, então o Cosmos, ao arrefecer após o Big Bang, ficaria “preso” nesse estado e teria, necessariamente, de sofrer uma expansão acelerada³. Rapidamente percebeu a implicação desta conclusão, nomeadamente que muitos dos problemas do modelo quente do Big Bang seriam resolvidos, e designou esta fase como inflação. Mas como ocorreria essa expansão? Na realidade, um estado de falso vácuo que se expanda exponencialmente permite que o verdadeiro vácuo (estado de menor energia) apareça por via de nucleação de bolhas, como na FIGURA 1, sendo que a perda de energia dentro das bolhas é compensada pela energia na superfície das mesmas (semelhante a uma tensão superficial dos fluidos). Esta energia é libertada nos processos de colisão entre bolhas. O processo continua até que todas as bolhas tenham colidido e o espaço esteja totalmente no verdadeiro vácuo. Contudo, para que a inflação tenha tempo suficiente para resolver os problemas do Big Bang quente, tem de haver poucos processos de nucleação de bolhas e as colisões serem raras, algo característico numa expansão exponencial. Assim, não haveria energia suficiente para que o Universo reaquecesse, tornando-o excessivamente frio e incompatível com as observações.

De facto, existem outros intervenientes pioneiros nos estudos iniciais de uma fase inflacionária, muitas vezes esquecidos nas tramas e urdumes da malha da história: o astrofísico grego Demosthenes Kazanas, o físico japonês Katsuhiko Sato e o seu colaborador e físico norte-americano Martin Einhorn^{4, 5}. O primeiro havia sugerido, em 1980, que uma transição de fase no Universo primordial associada a uma quebra espontânea de simetria de uma Teoria de Grande Unificação poderia levar a uma expansão exponencial e, se durasse um tempo suficiente, potencialmente explicaria a isotropia observada do Universo⁶. Por seu turno, Katsuhiko Sato, em 1981, sugeriu que uma expansão acelerada poderia eliminar o problema das paredes de domínio⁷ e, no mesmo ano, em colaboração com Einhorn publicou um modelo que resolvia o problema dos monopólos magnéticos⁸. Este último modelo, semelhante ao de Guth, também padecia dos mesmos problemas: um valor muito específico para a constante cosmológica e muitas bolhas de verdadeiro vácuo para que o período inflacionário resolvesse os problemas do modelo do Big Bang quente restantes.

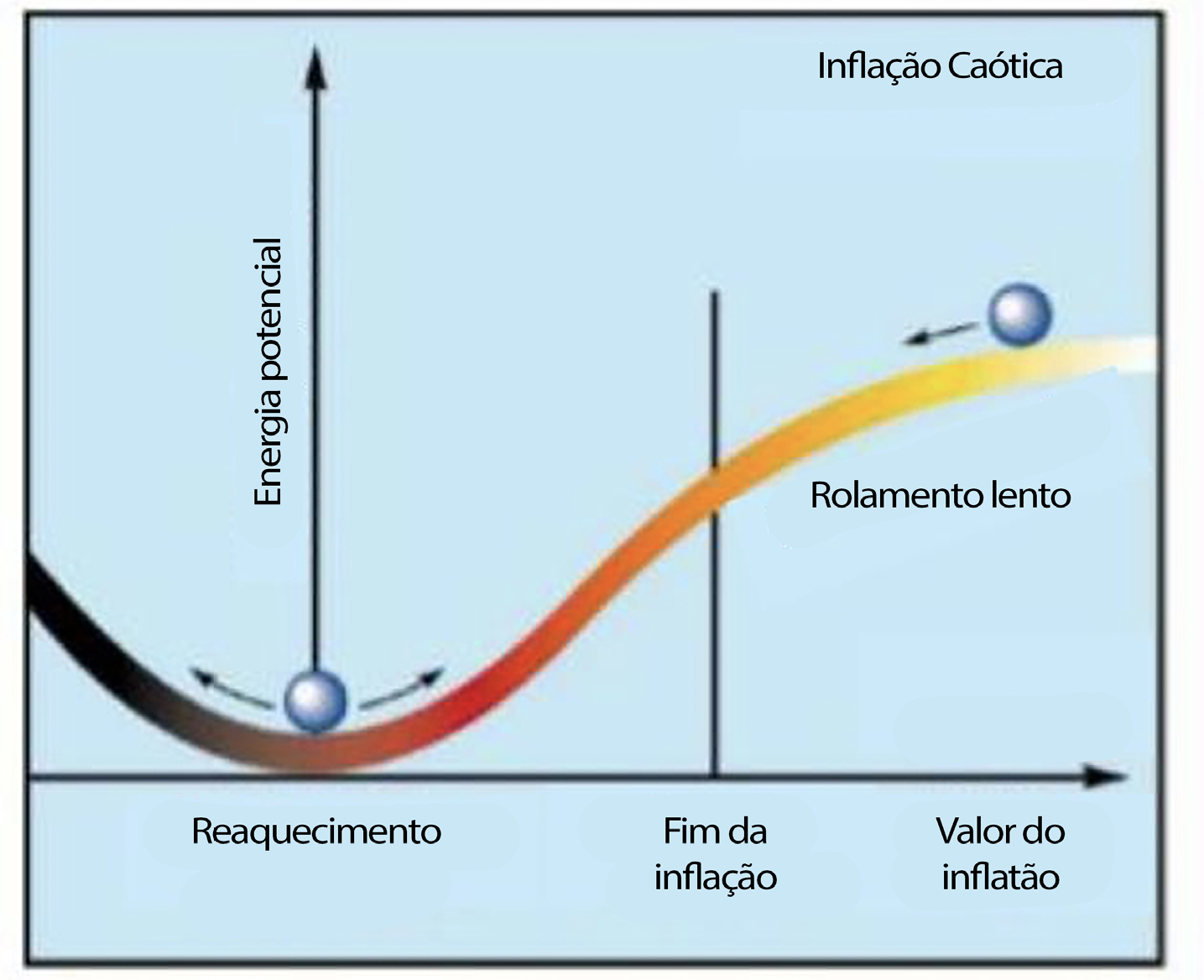
O físico russo Andrei Linde propôs uma solução para o problema da colisão das bolhas em 1982⁹, assim como o fizeram, independentemente, os físicos Andreas Albrecht e Paul Steinhardt num artigo no mesmo ano¹⁰. Esta nova solução passou a ser conhecida como Nova Inflação ou Inflação de “rolamento lento” (slow-roll inflation na terminologia inglesa), e, por conseguinte, a formulação anterior passou a ser chamada de Velha Inflação. Assim, a nova ideia parte da consideração de um dado campo escalar, cuja flutuação quântica associada é a partícula inflatão, que rola muito lentamente ao longo do seu potencial em direção ao mínimo do mesmo. Durante este processo, o Universo expande e, quando o inflatão desce a parte mais pronunciada do seu potencial, a inflação termina e começa o processo de reaquecimento. Este modelo tem a vantagem de resolver os problemas da Velha Inflação, proporcionando uma “saída limpa” (graceful exit na terminologia inglesa), todavia introduzindo outros, nomeadamente, a assumpção de que o Universo teve de estar num estado pré-inflacionário extremamente quente e que a inflação estava intimamente ligada a uma transição de fase cosmológica.

Um ano mais tarde, em 1983, Linde propôs um cenário mais geral que os dois cenários anteriores aqui discutidos: a inflação caótica¹¹ (FIGURA 2). Este modelo foi criado com base nas ideias e conclusões de Steinhardt de que o cenário da Nova Inflação poderia incluir a possibilidade de o processo inflacionário ser eterno, isto é, numa dada região poder terminar, mas noutra região do espaço continuar a expandir-se, e nas conclusões de Alexander Vilenkin de que efeitos quânticos promovem essa possibilidade de inflação eterna¹². Assim, a proposta de inflação caótica de Linde tem a vantagem de não requerer a existência de um equilíbrio térmico inicial.

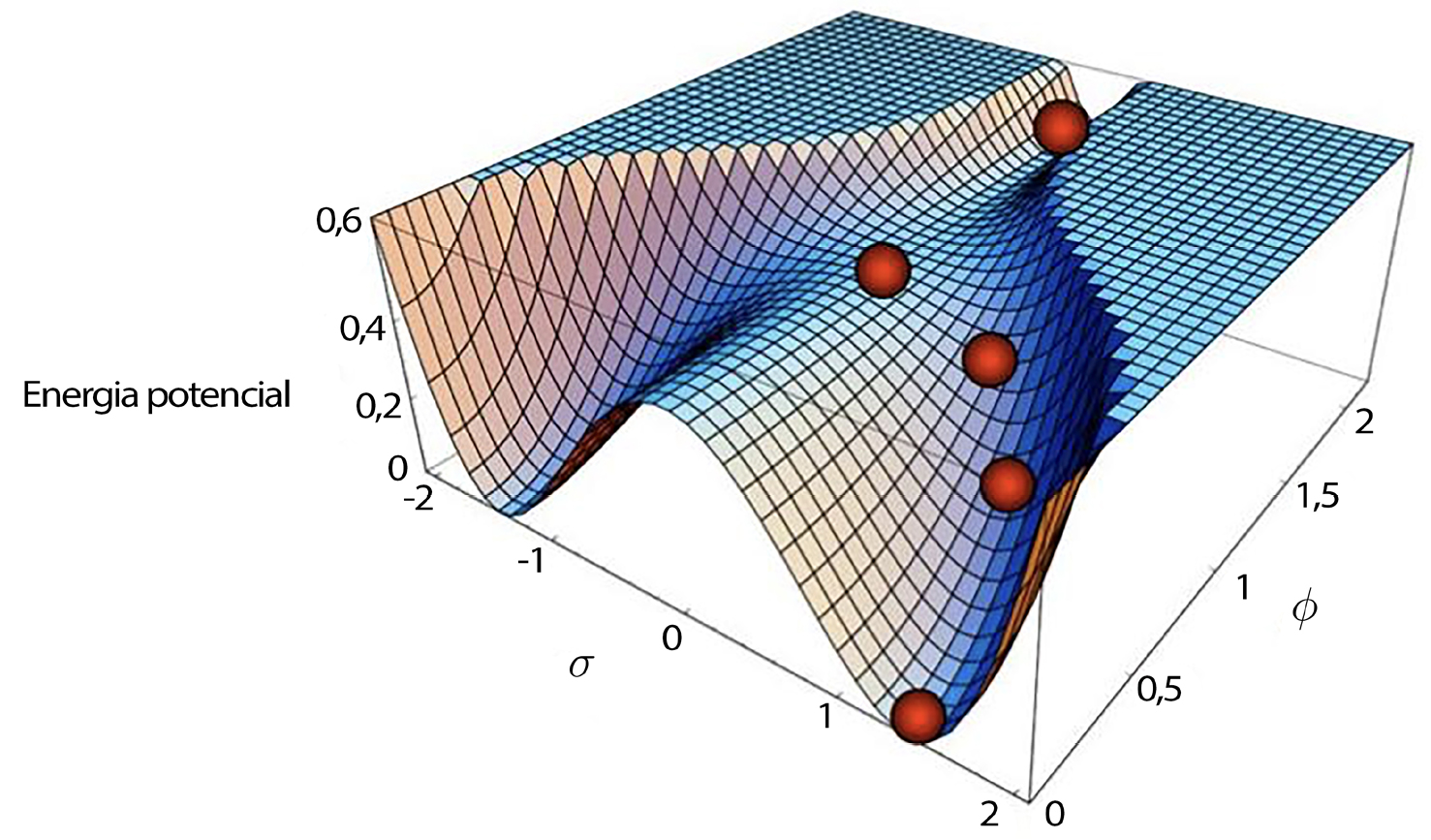
Em 1994, Linde propôs um outro modelo inflacionário: a inflação híbrida, na qual um dado campo escalar rola rapidamente devido à presença de um campo adicional, sendo que a inflação termina naturalmente quando termina o slow-roll¹⁴ (FIGURA 3).

Quando a inflação termina, existe um período chamado reaquecimento (reheating na terminologia inglesa), uma vez que o inflatão decai em partículas do Modelo Padrão da Física de Partículas que preenchem o Universo. Assim, a radiação eletromagnética emitida é a componente dominante desta fase cósmica. Assim, as flutuações quânticas inflacionárias adquirem dimensões cosmológicas, sendo as sementes da formação de estruturas do nosso Universo.

Sendo a inflação cósmica um paradigma e não uma teoria, significa que existem muitos modelos que prevêem uma fase inicial de rápida expansão. Felizmente, há também dados observacionais muito precisos que permitem excluir ou constranger um dado modelo, principalmente pelos dados da radiação cósmica de fundo obtidos pelas missões COBE, WMAP e, mais recentemente, Planck. Assim, esta época cósmica é particularmente relevante para estudar modelos gravitacionais de altas energias ou que permitem explicar os problemas da matéria escura e da energia escura^{16, 17, 18}.