A Aritmética, a Álgebra, a Geometria, a Trigonometria, a Cosmografia e a Geografia Matemática são disciplinas que fizeram parte do ensino e sofreram várias reformulações ao longo dos séculos XIX e XX, tendo havido uma fusão destas áreas no final da década de quarenta do século XX até à década de setenta. A Trigonometria, que estava incluída na aplicação à Topografia, foi a que menos alterações sofreu.

Os métodos de ensino da Matemática e as reformas na educação, na passagem do século XIX para o século XX, foram tema de debates internacionais e nacionais. Neste período, encontravam- se, nos manuais, descrições de instrumentos utilizados na época e do modo como eram usados. Posteriormente, estas descrições transformaram-se em pequenas notas informativas, reduzindo-se o número de problemas de aplicação da Trigonometria¹.

Em Portugal, José Joaquim Manso-Preto dedica a segunda parte do seu manual² à descrição e uso de instrumentos utilizados nas operações trigonométricas. O grafómetro, na opinião daquele autor, é um dos principais instrumentos para trabalhar no terreno, sendo o fio de prumo e o nível de bolha de ar referidos como auxiliares das medições com ele. Na época, conhecer e saber utilizar instrumentos era condição necessária para a aprovação de candidatos à docência da Matemática e, nas primeiras décadas do século XX, discutiu-se a possibilidade de introduzir no ensino da Matemática a moderna orientação de utilização do “método de laboratório”¹. Com este método pretendia-se que os alunos construíssem instrumentos simples e que os utilizassem em medições de alturas, leitura de ângulos, etc.. O relato desta experiência foi feito por Ruy da Silva Leitão e encontra-se publicado na Gazeta de Matemática³.

Grafómetro.

O grafómetro (FIGURA 1) é um instrumento usado para medir ângulos do qual podemos dizer que é uma consequência da evolução da Dioptra e um antecessor imediato do teodolito. Desde a sua invenção em 1597, tem sido destacado pela sua simplicidade e resistência. Foi ainda, utilizado por agrimensores e geómetras, desde meados do século XVII ao final do século XIX, em várias operações como medições de terrenos, entre outras⁴. A sua invenção foi atribuída a Philippe Danfrie⁵, um inventor e fabricante de instrumentos matemáticos em metal e papel, datilógrafo, editor e autor. Cerca de quarenta anos após o aparecimento do primeiro instrumento, Danfrie escreveu, projetou e publicou um tratado sobre o grafómetro — Declaration de l’usage du graphometre⁶.

Segundo uma descrição de José Joaquim Manso-Preto² o instrumento (FIGURA 1) consiste num semicírculo \(ADB\), normalmente em latão, designado por limbo e está dividido em 180 graus. Designa-se por linha de fé a reta traçada sobre o diâmetro \(ACB\) e que passa nos pontos 0 e 180 graus. Tem, para além do diâmetro fixo, um outro \(EE′\), formado por uma peça metálica em forma de régua que é móvel em torno de \(C\) e em que a sua extremidade \(E\) pode percorrer todas as divisões do limbo — designa-se por alidade.

Podemos ainda ver aplicadas perpendicularmente duas pínulas (FIGURA 2) nas extremidades do diâmetro fixo e da alidade. Estas duas peças metálicas retangulares apresentam duas aberturas, uma fenda e outra mais larga, que é atravessada por um fio fino de seda ou metal colocado sobre o prolongamento da fenda com o objetivo de estabelecer os alinhamentos.

Na parte de baixo (FIGURA 1) encontra-se uma esfera contida em dois hemisférios ocos \(G\), que se podem apertar ou alargar por meio de um parafuso de pressão. Esta peça, designada por joelho, permite dar ao grafómetro todas as posições que se pretenda. O instrumento é sustentado sobre um pé \(TSUVZ\), composto por três pernas \(U\), \(V\), \(Z\) móveis em \(S\). No centro do instrumento encontra-se uma bússola para orientar os objetos.

Medir com um grafómetro.

Pedro-Manso explica que para, por exemplo, medir o ângulo \(FCH\) (FIGURA 3) formado pelos ângulos de visão tirados pelo ponto \(C\) para os objetos \(F\) e \(H\), coloca-se o centro do grafómetro no ponto \(C\), designado por centro da estação, e gira-se o plano do limbo até que fique na direção do plano que passa pelos pontos \(C\), \(F\) e \(H\). De seguida, dirigem-se os fios (que passam pelas pínulas) do diâmetro fixo e da alidade para cada um dos objetos de forma que os objetos fiquem no cruzamento dos dois fios. O arco compreendido entre os dois diâmetros do instrumento será a medida do ângulo \(FCH\). A fiabilidade da leitura do instrumento pode ser testada medindo os três ângulos internos de um triângulo, cujos vértices sejam três pontos sobre o terreno, e ver se a soma dos ângulos observados é 180 graus.

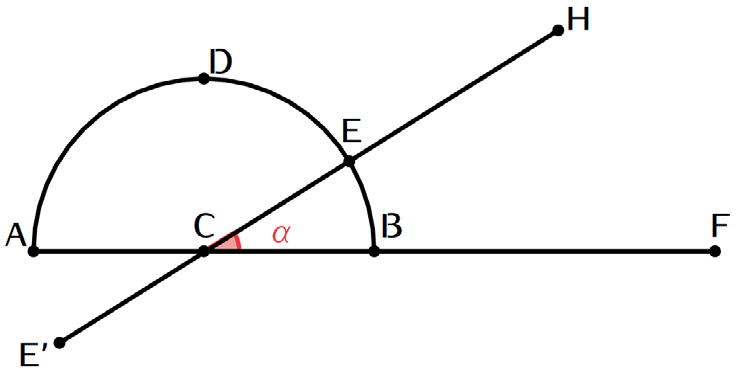
Aplicações — problemas da Topografia.

O papel inicial da Trigonometria está associado à resolução de problemas que podiam ser relacionados com triângulos e o seu estudo desenvolveu-se a partir da necessidade sentida por diversos povos em áreas como a Navegação, Agrimensura e Topografia. Os primeiros indícios surgiram na Babilónia com o cálculo de razões entre números e entre lados de triângulos semelhantes⁷. A Trigonometria define-se como sendo a parte da Matemática que ensina a medir os lados e os ângulos dos triângulos, chegando mesmo a ser considerada uma extensão da Geometria.

No entanto, a grande instigadora do desenvolvimento da Trigonometria foi a Astronomia. O astrónomo grego Hiparco (190 a.C.—120 a.C.), fortemente influenciado pela Matemática Babilónica, é geralmente descrito como o “pai da Trigonometria” uma vez que construiu a que se pode chamar de primeira tabela trigonométrica, mas foi Ptolomeu (125 a.C.) quem, baseado nos trabalhos de Hiparco, apresenta um verdadeiro tratado de Trigonometria plana e esférica — o Almagesto⁷.

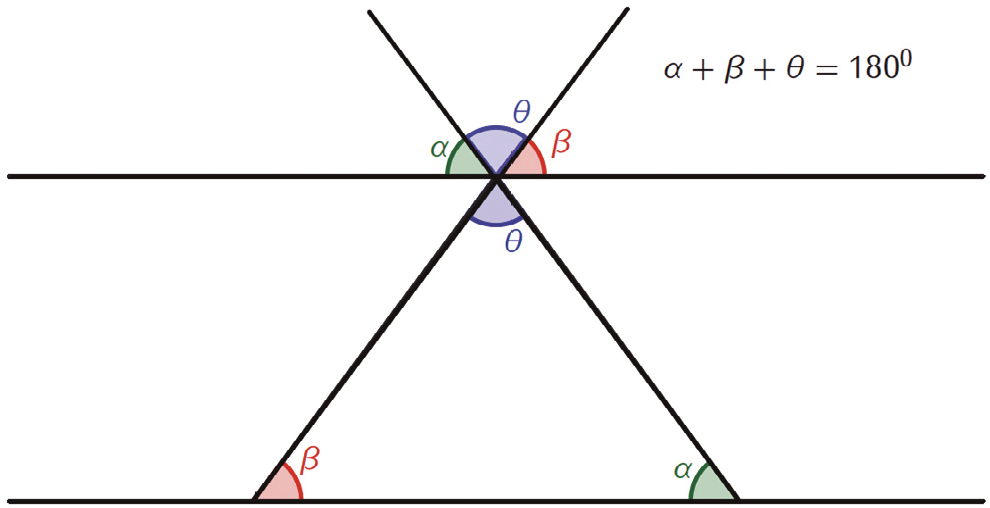
Na Trigonometria plana consideramos triângulos formados sobre um plano pela interseção de três linhas. Os três ângulos são designados por \(A\), \(B\) e \(C\), e os lados opostos por \(a\), \(b\) e \(c\). Para apoiar a resolução das aplicações selecionadas, destaca-se três teoremas enunciados por Manso — Preto²:

1. “Em todo o triângulo (...) a soma dos três ângulos internos equivale a dois retos.” (FIGURA 4).
2. “Em todo o triângulo retângulo, um cateto é igual à hipotenusa multiplicada pelo seno do ângulo oposto ao mesmo cateto.”.








Considere a FIGURA 5. Seja \(ACB\) um triângulo retângulo em \(A\), \(BD = 1\) e \(DE\) perpendicular a \(AB\) no ponto \(E\) (será o seno do ângulo \(ABC\)).









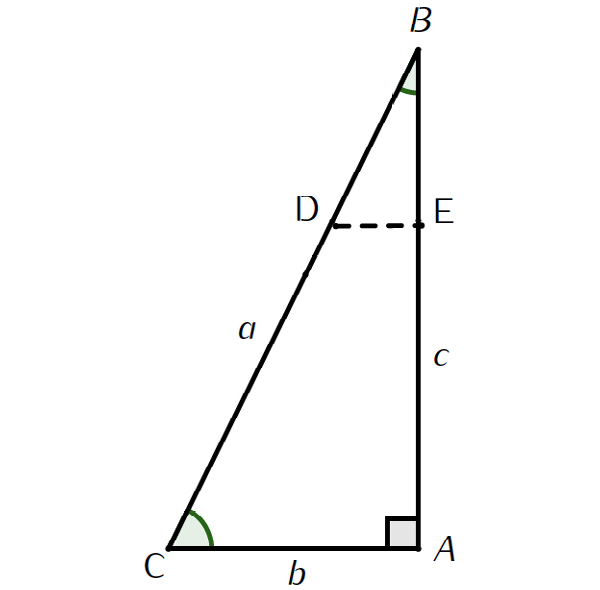
Uma vez que os triângulos \(ABC\) e \(EBD\) são semelhantes, temos:




\(\frac{BD}{DE}=\frac{BC}{AC}\)




ou,




\(\frac{1}{\textrm{sen}(B)}=\frac{a}{b}\Leftrightarrow b=a\;\textrm{sen}(B)\)




Analogamente,




\(\frac{1}{\textrm{sen}(C)}=\frac{a}{c}\Leftrightarrow c=a\;\textrm{sen}(C)\)



3. “Em todo o triângulo (...) os lados são proporcionais aos senos dos ângulos opostos.”.

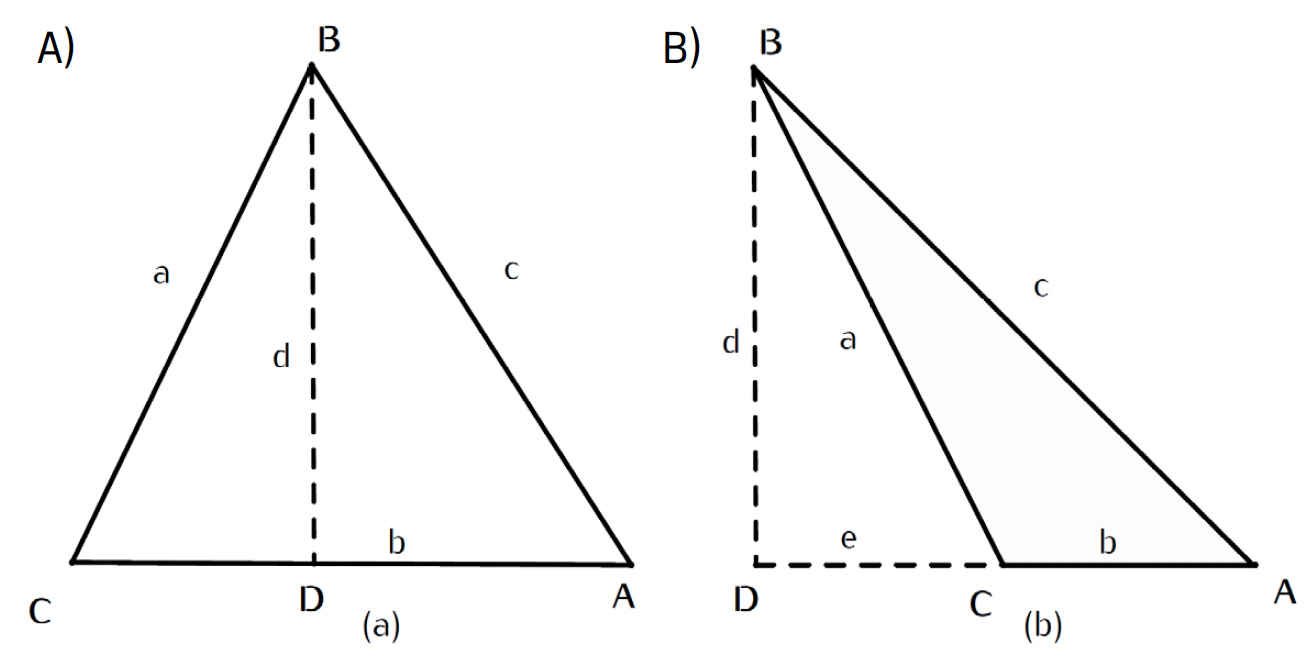
Considere-se o triângulo \(ACB\) representado na FIGURA 6. Por qualquer um dos vértices, baixamos uma perpendicular, seja \(BD\), segundo a figura. Dos dois triângulos retângulos \(CBD\) e \(ABD\) obtemos obtemos (Teorema 2):










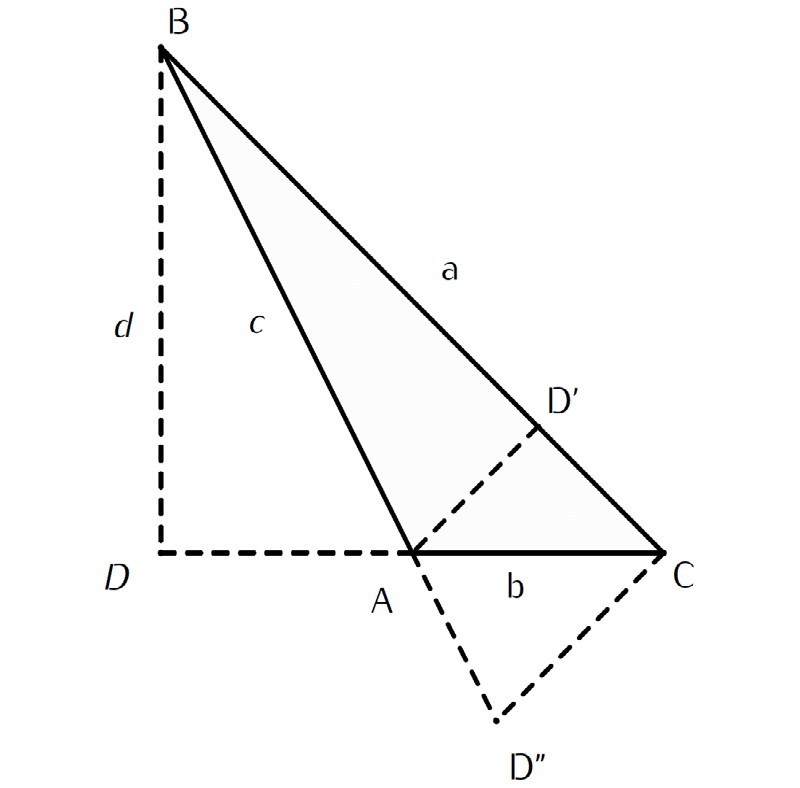
\(BD=d=a\;\textrm{sen}(C)=c\;\textrm{sen}(BAD)\)




Como os ângulos \(BAD\) e \(BAC\) (ou simplesmente \(A\)) são suplementares temos:




\(d=a\;\textrm{sen}(C)=c\;\textrm{sen}(A)\)




O que resulta,




\(\frac{a}{c}=\frac{\textrm{sen}(A)}{\textrm{sen}(C)}\).




Da mesma forma obtemos,




\(\frac{a}{b}=\frac{\textrm{sen}(A)}{\textrm{sen}(B)}\) e \(\frac{b}{c}=\frac{\textrm{sen}(B)}{\textrm{sen}(C)}\).



4. “Em todo o triângulo (...) o quadrado feito sobre um qualquer dos seus lados é igual à soma dos quadrados feitos sobre os outros dois lados menos o dobro do retângulo por eles compreendido, multiplicado pelo coseno do ângulo oposto ao primeiro lado.”.

Considere-se o triângulo \(ABC\) (FIGURA 7A) ângulo \(C\) agudo e FIGURA 7B) ângulo \(C\) obtuso). De qualquer um dos vértices, considere-se \(B\), baixamos sobre o lado oposto ou sobre o lado produzindo a perpendicular \(BD\), designada por \(d\). Da FIGURA 7B) derivamos as seguintes equações:

\(c^2=f^2+d^2\)

\(a^2=e^2+d^2\)

\(f=e+b\)

\(\textrm{cos}(C)=-\frac{e}{a}\) (o cosseno de um ângulo obtuso é a negação do cosseno de seu suplemento). Assim temos,

\(c^2=f^2+d^2=(e+b)^2+d^2=e^2+2eb+b^2+d^2=a^2+b^2-2ab\;\textrm{cos}(C)\)

De forma idêntica obtemos,

\(b^2=a^2+c^2-2ac\;\textrm{cos}(B)\) e \(a^2=b^2+c^2-2bc\;\textrm{cos}(A)\).

No seu manual, Manso-Preto², fala-nos de algumas aplicações da Topografia, a ciência que tem por objetivo a descrição exata de um lugar. Os métodos clássicos da Topografia, baseiam- -se na medição de ângulos e distâncias recorrendo a instrumentos de medição, como é exemplo o grafómetro.

Triangulação.

A operação de recolha de informação necessária para a elaboração de uma planta de uma região é designada por levantamento topográfico. Para fazer o levantamento de uma pequena extensão de terreno, identificamos pontos notáveis que, por simplificação, vamos supor estarem todos situados no mesmo plano horizontal. Supomos que todos estes pontos se encontram ligados por linhas retas de modo a obter uma rede de triângulos que cobre todo o terreno que se pretende levantar. Com o auxílio de um grafómetro medem-se todos os ângulos desses triângulos e definimos, preferencialmente, o lado maior como base.

Manso-Preto exemplifica com o esquema da FIGURA 8. Considera que com os pontos \(A\), \(B\), \(C\), \(D\),... forma-se uma rede de triângulos dos quais se pretende calcular os lados. Considera-se como base o lado maior \(AB\), mede-se esta distância e numa das extremidades coloca-se o grafómetro de forma que o centro corresponda ao ponto \(A\), e que o diâmetro fixo se ajuste com \(AB\), dirige-se a alidade móvel sobre os objetos \(E\), \(F\) e \(G\), e anota-se o valor dos ângulos \(\measuredangle BAE\), \(\measuredangle BAF\) e \(\measuredangle BAG\).

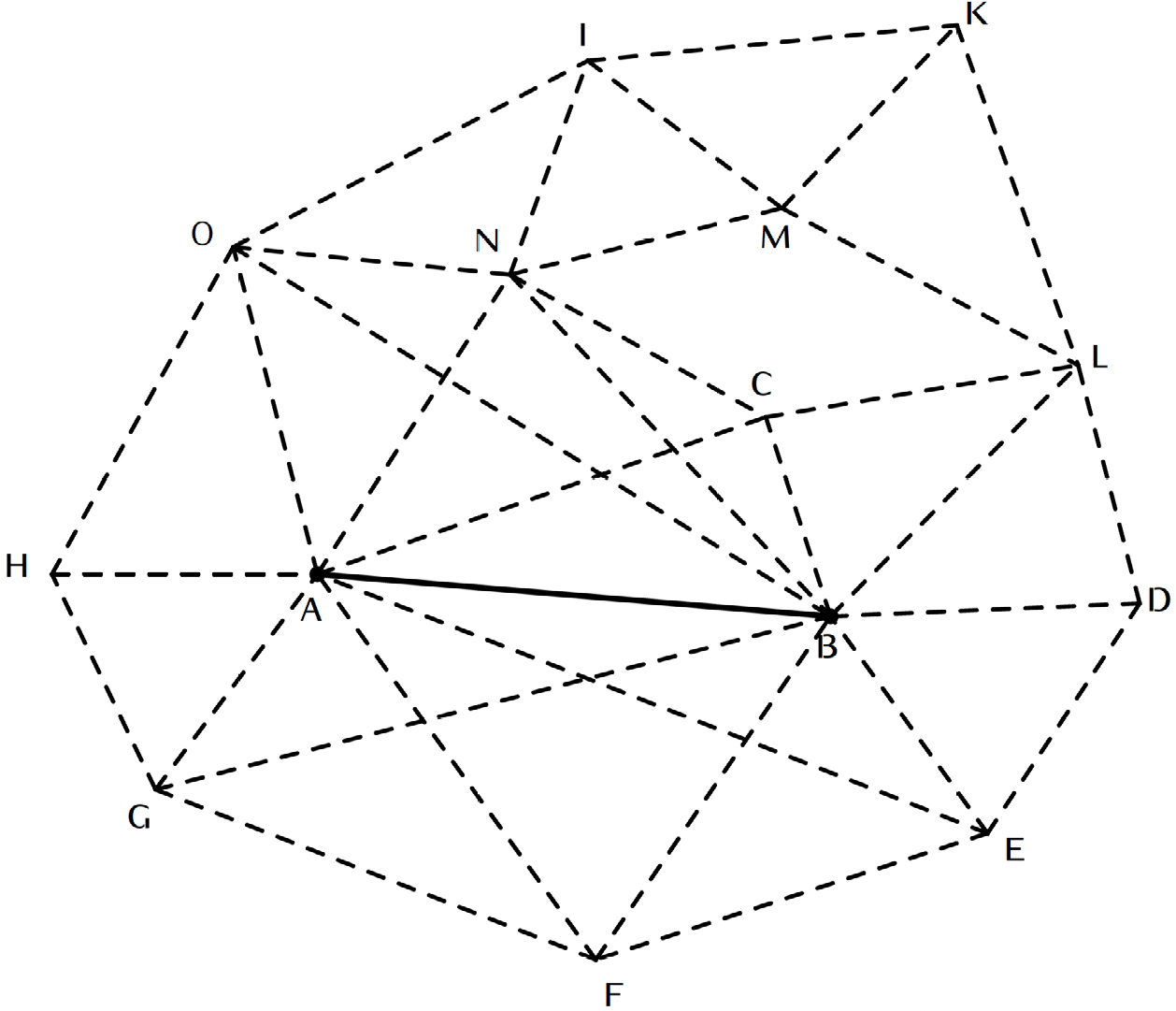
Mantendo o grafómetro na mesma posição, coloca-se o diâmetro fixo sobre \(AG\) e a alidade móvel sobre o ponto \(H\) e anota-se o valor do ângulo \(\measuredangle GAH\). Faz-se este procedimento para todos os pontos observados de \(A\) e procuramos a soma dos ângulos observados e existentes em torno deste ponto (deverá ser igual a 360 graus). De seguida, transporta-se o grafómetro para o outro extremo \(B\) da base \(AB\) e procede-se da mesma forma para os pontos \(L\), \(M\), \(N\),..., percorrendo desta forma toda a extensão de terreno que se pretende fazer o levantamento da planta.

Medidos os ângulos dos triângulos e a base \(AB\), temos conhecidos os ângulos e o lado \(AB\) do triângulo \(ABC\), podendo assim calcular os outros dois lados \(AC\) e \(BC\), que irão ser considerados como bases dos novos triângulos \(ANC\) e \(BCL\) ao qual se procede da mesma forma até calcular todos os ângulos e lados de todos os triângulos.

Feitas todas as medições dos ângulos e calculados todos os lados dos triângulos, com a ajuda da régua e do transferidor é feito um esquema em papel da figura e proporções do terreno de que pretendíamos levantar a planta.

Determinar a altura de uma montanha.

A determinação da altura de uma montanha é um dos exemplos (FIGURA 9) tratados no manual de 1860 de Manso-Preto, de aplicação do principal instrumento utilizado para medir ângulos sobre o terreno.

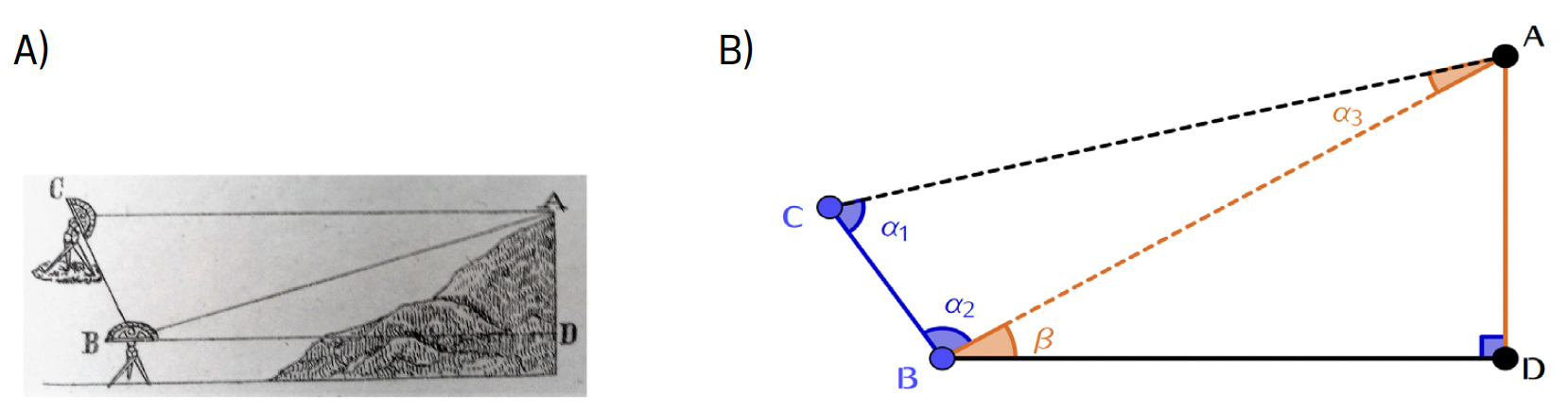
Assim, e a alguma distância da montanha, medimos uma base, seja \(BC\) e observamos com o grafómetro os ângulos \(\measuredangle ACB=\alpha_1\) e \(\measuredangle ABC=\alpha_2\) formados entre a base \(BC\) e o cume \(A\) da montanha. Identificamos o triângulo \(ABC\) e calculamos \(AB\).

Do Teorema 1, resulta que o ângulo \(\measuredangle CAB=\alpha_3\) é dado por

\(\alpha_3=180^{\circ}-\left ( \alpha_1+\alpha_2 \right )\)

e o valor de \(AB\) resulta do Teorema 3, e é dado por

\(AB=\frac{BC\;\textrm{sen}\left ( \alpha_1 \right )}{\textrm{sen}\;\left ( \alpha_3 \right )}\).

Obtido o valor de \(AB\), observamos com o grafómetro o ângulo \(\measuredangle ABD=\beta\) formado pela linha formada pelo raio visual \(AB\) com a horizontal \(BD\). Imaginamos a vertical \(AD\) e temos um triângulo retângulo \(ABD\) com o ângulo agudo \(\beta\) e a hipotenusa \(AB\), assim assim pelo Teorema 2, temos que:

\(AD=AB\;\textrm{sen}(\beta)\).

Adicionamos à altura \(AD\) a altura do instrumento acima do solo e obtemos a altura da montanha.

Encontrar a distância entre dois pontos inacessíveis.

Um outro exemplo de utilização do grafómetro é na determinação da distância entre dois pontos inacessíveis. Na FIGURA 10 observamos os pontos \(A\) e \(B\) inacessíveis e escolhemos uma base \(CD\) onde, a partir de \(C\) observamos os ângulos \(\measuredangle ACD\) e \(\measuredangle BCD\) e a partir de \(D\) observamos os ângulos \(\measuredangle ADC\) e \(\measuredangle BDC\).

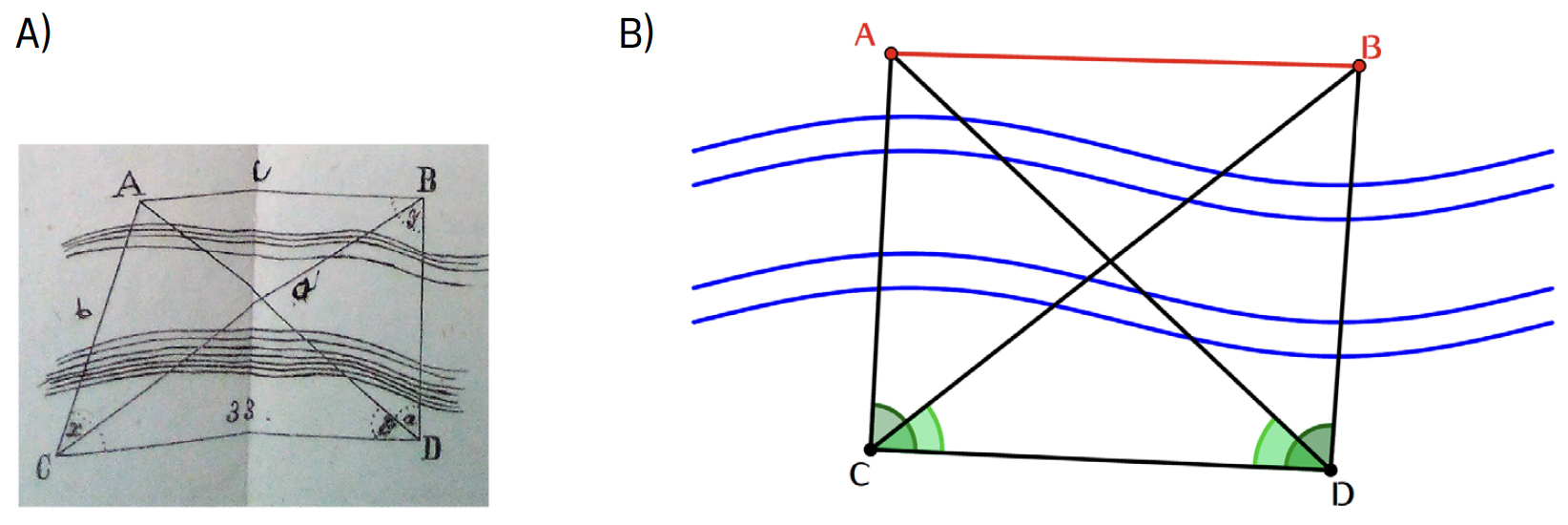
Uma vez que, no triângulo \(ACD\) são conhecidos o lado \(CD\) e os dois ângulos adjacentes \(\measuredangle ACD\) e \(\measuredangle ADC\) podemos calcular o lado \(AC\) utilizando o Teorema 3.

\(\frac{CD}{AC}=\frac{\textrm{sen}\left ( \measuredangle CAD \right )}{\textrm{sen}\left ( \measuredangle ADC \right )}=\frac{\textrm{sen}\left ( 180^{\circ}-\left ( \measuredangle ACD+\measuredangle ADC \right ) \right )}{\textrm{sen}\left ( \measuredangle ADC \right )}\)

\(AC=\frac{CD\;\textrm{sen}\left ( \measuredangle ADC \right )}{\textrm{sen}\left ( 180^{\circ}-\left ( \measuredangle ACD+\measuredangle ADC \right ) \right )}\).

De forma análoga, podemos calcular o lado \(BC\), dado que, no triângulo \(BCD\) são conhecidos o lado \(CD\) e os dois ângulos adjacentes \(\measuredangle BCD\) e \(\measuredangle BDC\) e pelo mesmo teorema temos que

\(\frac{CD}{BC}=\frac{\textrm{sen}\left ( \measuredangle CBD \right )}{\textrm{sen}\left ( \measuredangle BDC \right )}=\frac{\textrm{sen}\left ( 180^{\circ}-\left ( \measuredangle BCD+\measuredangle BDC \right ) \right )}{\textrm{sen}\left ( \measuredangle BDC \right )}\)

\(BC=\frac{CD\;\textrm{sen}\left ( \measuredangle BDC \right )}{\textrm{sen}\left ( 180^{\circ}-\left ( \measuredangle BCD+\measuredangle BDC \right ) \right )}\).

Se os pontos \(A\), \(B\), \(C\) e \(D\) estão no mesmo plano, o ângulo \(\measuredangle ACB\) é dado por \(\measuredangle ACB=\measuredangle ACD-\measuredangle BCD\), senão terá que ser observado.

Uma vez que, são conhecidos os lados \(AC\) e \(BC\) e o ângulo \(\measuredangle ACB\) do triângulo ABC, aplicando o Teorema 4, podemos calcular a distância \(AB\) entre os pontos inacessíveis \(A\) e \(B\):

\(AB^2=AC^2+BC^2-2AC.BC.\cos\left ( \measuredangle ACB \right )\).

Manso-Preto não apresenta estes cálculos, mas espera que o leitor seja capaz de os fazer.

O grafómetro é um instrumento matemático devido à sua capacidade de quantificar e medir grandezas. Quando começou a crescer o número de instrumentos matemáticos, também cresceu a dedicação à geometria prática, nomeadamente na Topografia. No século XX, no guia para a utilização do Compêndio de Matemática⁸, Sebastião e Silva indicava que “A introdução à trigonometria poderá e deverá ser feita com motivação concreta, apta a despertar interesse suficiente no espírito do aluno.”. Assim, algumas das ideias de Manso-Preto foram mais tarde, na década de sessenta, encontradas nos textos de Sebastião e Silva, elaborados no âmbito do projeto de modernização do ensino da matemática do 3.º ciclo com impacto nacional e internacional¹. O projeto defendia uma reforma curricular que teria que ser realizada reestruturando os programas e os métodos de ensino. O autor preocupava-se com o estado do ensino da matemática em Portugal e nos seus textos⁸, falavam dos problemas que identificava no ensino, afirmando que: “O nosso ensino tradicional não enferma unicamente da fraca (e quantas vezes nula) insistência em demonstrações, e de insuficiente rigor lógico: peca também por ausência de contacto com o húmus da intuição e com a realidade concreta.”. Sebastião e Silva propõe problemas clássicos tais como calcular a altura de uma torre por meio de medições efetuadas no solo (sem subir à torre)⁸, achar a largura de um rio por meio de medições efetuadas numa das margens (sem atravessar o rio)⁸ e calcular a altura de uma torre, por meio de medições efetuadas no solo, em plano horizontal, supondo que a base é visível, mas não é acessível⁸.

Na pesquisa sobre o uso de instrumentos matemáticos antigos em sala de aula observamos que os diferentes procedimentos de medição são importantes tanto na formação de professores como nas atividades desenvolvidas com os alunos de forma a conseguirem justificar os seus argumentos e validar as suas escolhas.