O Problema.

Considere as funções \(f\) e \(g\), de domínio \(\left ] 0,+\infty \right [\), definidas for \(f\left ( x \right )=\frac{k}{x}\) e por \(g\left ( x \right )=-\frac{k}{x}\), com \(k > 0\).

Considere ainda:

• Dois pontos \(P\) e \(Q\), com a mesma abcissa, pertencentes, respetivamente, ao gráfico da função \(f\) e ao gráfico da função \(g\);
• A reta \(s\), tangente ao gráfico da função \(f\) no ponto \(P\);
• A reta \(t\), tangente ao gráfico da função \(g\) no ponto \(Q\);
• O ponto \(R\), ponto de intersecção das retas \(s\) e \(t\).

Mostre que, qualquer que seja a abcissa dos pontos \(P\) e \(Q\), a área do triângulo \(\left [ PQR \right ]\) é igual a \(k\).

Primeiras impressões.

Neste problema, é com relativa tranquilidade que se percebe que a condição \(f = −g\) e \(f\left ( x \right )\neq 0\) para todo o \(x\in D_f\) é suficiente para que \(R\) tenha a sua existência garantida no eixo \(O_x\).

E isto é claro porque sabemos que \(f'\left ( x \right )\neq 0\) em todo o domínio considerado. Caso \(f'\left ( x \right )= 0\), para algum \(x\), o ponto \(R\) deixaria de existir (assim como o \(\Delta\left [ PQR \right ]\)). As imagens abaixo ilustram as duas situações para a função \(f\left ( x \right )=e^{\sin x}+2\).

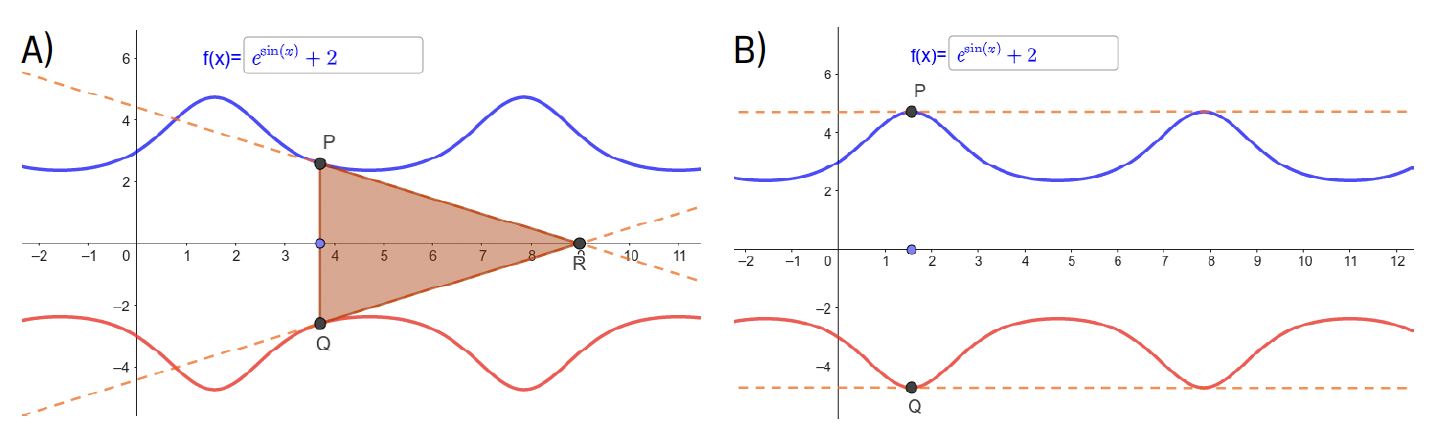
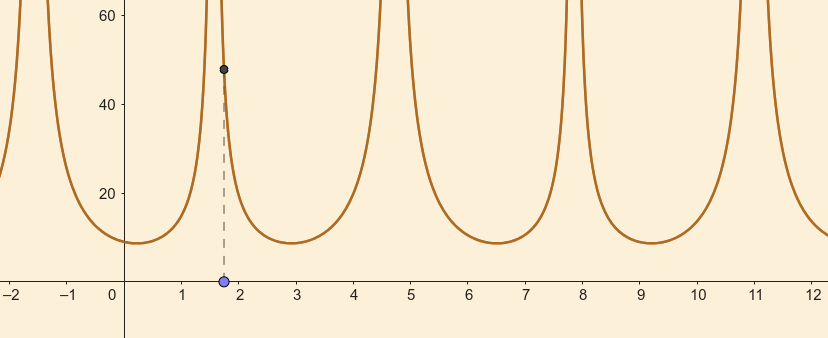
Note-se que, em geral, como se pode ver pelas FIGURAS 1 e 2, a área do triângulo \(\left [ PQR \right ]\) não é constante, quando a abcissa de \(P\) e \(Q\) varia, ao contrário do que acontece no Problema 16 para a função \(f\left ( x \right )=\frac{k}{x}\). Em geral, quando \(f'\left ( \alpha \right )=0\), a área “explode” para \(\infty \) para valores de \(x\) muito próximos de \(\alpha\).

O leitor pode, se entender, manipular a construção GeoGebra, experimentando outras funções a seu gosto. Casos que podem ser interessantes de experimentar:

\(f\left ( x \right )=e^x;f\left ( x \right )=\tan \left ( x \right );f\left ( x \right )=\frac{20}{x-2};f\left ( x \right )=5;\)

\(f\left ( x \right )=x^n;f\left ( x \right )=\tan^n\left ( x \right );f\left ( x \right )=\sin ^n\left ( x \right )\left ( n\geq 2 \right )\)

Generalizações.

A função \(f\) que surge no Problema 16, e a área constante que daí resulta, é apenas um caso particular do seguinte resultado.

Teorema 1: Área do triângulo.

Seja \(f\) uma função diferenciável num intervalo aberto de \(\mathbb{R}\). Considere ainda:

1. Dois pontos \(P\) e \(Q\), com a mesma abcissa \(\alpha\), pertencentes, respetivamente, aos gráficos de \(f\) e \(−f\);
2. A reta \(s\), tangente ao gráfico da função \(f\) no ponto \(P\);
3. A reta \(t\), tangente ao gráfico da função \(−f\) no ponto \(Q\);
4. O ponto \(R\), ponto de intersecção das retas \(s\) e \(t\).

Então, a área do triângulo \(\left [ PQR \right ]\) é dada por \(A\left ( \alpha \right )=\frac{f\left ( \alpha \right )^2}{\left | f'\left ( \alpha \right ) \right |}\), para todo o \(\alpha\in D_f\) que satisfaça a condição \(f'\left ( \alpha \right )\neq 0\).

Demonstração.

Equações das retas \(s\) e \(t\):

\(s:y=f'\left ( \alpha \right )\left ( x-\alpha \right )+f\left ( \alpha \right )\)

\(t:y=-f'\left ( \alpha \right )\left ( x-\alpha \right )-f\left ( \alpha \right )\) (1)

A interseção das retas apenas não ocorre se \(f'\left ( \alpha \right )=0\), pois nesse caso \(s\parallel t\), que serão coincidentes caso \(\alpha\) seja simultaneamente um zero de \(f\). Daqui para a frente admitimos que \(f'\left ( \alpha \right )\neq 0\), para todo \(\alpha\in D_f\). Sendo \(R\left ( x,y \right )\), das equações (1) resulta que

\(y=-f'\left ( \alpha \right )\left ( x-\alpha \right )-f\left ( \alpha \right )=-\left [ f'\left ( \alpha \right )\left ( x-\alpha \right )+f\left ( \alpha \right ) \right ]=-y\Leftrightarrow y=0\) (2)

O que significa que o ponto \(R\) vive no eixo \(O_x\), sendo a sua abcissa, \(x\), a solução da equação (\(\alpha\) fixo):

\(0=f'\left ( \alpha \right )\left ( x-\alpha \right )+f\left ( \alpha \right )\)

Resolvendo-a,

\(0=f'\left ( \alpha \right )\left ( x-\alpha \right )+f\left ( \alpha \right )\)

\(0=f'\left ( \alpha \right )x-\alpha f'\left ( \alpha \right )+f\left ( \alpha \right )\) (3)

\(x=\frac{\alpha f'\left ( \alpha \right )-f\left ( \alpha \right )}{f'\left ( \alpha \right )}=\alpha -\frac{f\left ( \alpha \right )}{f'\left ( \alpha \right )}\)

Segue-se de (2) e (3) que \(R\) tem de coordenadas \(R\left ( \alpha-\frac{f\left ( \alpha \right )}{f'\left ( \alpha \right )},0 \right )\). Assim, a área do triângulo \(\left [ PQR \right ]\) será dada por

\(A\left ( \alpha \right )=\frac{1}{2}\left | 2f\left ( \alpha \right )\left ( \alpha -\frac{f\left ( \alpha \right )}{f'\left ( \alpha \right )} \right ) \right |\Leftrightarrow A\left ( \alpha \right )=\frac{f\left ( \alpha \right )^2}{\left | f'\left ( \alpha \right ) \right |}\) (4)

No Problema 16, \(f\left ( x \right )=\frac{k}{x}\) e \(g\left ( x \right )=-f\left ( x \right )\), sendo que \(f\) é diferenciável e \(f'\left ( x \right )\neq 0\) no domínio considerado. Verificando o resultado (4),

\(A\left ( \alpha \right )=\frac{\left ( \frac{k}{\alpha} \right )^2}{\left | -\frac{k}{\alpha^2} \right |}=\frac{k^2}{\alpha^2}\times \frac{\alpha^2}{k}=k\)

Nota para reflexão:

A abcissa do ponto \(R\), \(x_a=\alpha-\frac{f\left ( \alpha \right )}{f'\left ( \alpha \right )}\), e a fórmula recursiva no método de Newton, \(x_{n+1}=x_n-\frac{f\left ( x_n \right )}{f'\left ( x_n \right )}\), não têm o mesmo aspeto por acaso, pois não? No caso particular da função \(f\left ( x \right )=\frac{k}{x},x_{n+1}=2x_n\), o que não surpreende mas traduz certas propriedades geométricas únicas presentes nas hipérboles, nomeadamente algumas relacionadas com áreas (voltaremos a este aspeto mais tarde, numa demonstração quase visual...).

Mais além...

Tal como observamos atrás, em geral, a área \(A_{\Delta}\left ( x \right )\) do triângulo \(\left [ PQR \right ]\) não é uma função constante.

Por exemplo, se \(f\left ( x \right )=e^{\sin \left ( x \right )}+2\) (FIGURA 1), basta observar que esta tem extremos para afirmar que a área do triângulo \(\left [ PQR \right ]\) varia. Neste exemplo, essa área é dada, para cada valor de \(x\in\mathbb{R}\setminus \left \{ \frac{\pi}{2}+t\pi,t\in\mathbb{Z} \right \}\), pela função \(A_{\Delta}\left ( x \right )=\frac{f\left ( x \right )^2}{\left | f'\left ( x \right ) \right |}=\frac{\left ( e^{\sin x}+2 \right )^2}{e^{\sin x}\left | \cos x \right |}\), cuja representação gráfica se encontra na FIGURA 2.

No entanto, no Problema 16 estamos perante uma função, \(f\left ( x \right )=\frac{k}{x}\), cuja função \(A_{\Delta}\left ( x \right )=k\) (constante!). Já sabemos que \(f\left ( x \right )=\frac{k}{x}\) é diferenciável e não tem extremos. Mas isso não chega para garantir que a área do triângulo \(\left [ PQR \right ]\) seja constante: a função \(f\left ( x \right )=e^x\) também é diferenciável e não tem extremos, no entanto \(A_{\Delta}\left ( x \right )=e^x\) (curioso!). Assim, a questão que se pode colocar é:

Quais são exatamente as funções que têm como função área associada, \(A_{\Delta}\left ( x \right )\), uma determinada constante \(k\) positiva?

A resposta está no seguinte resultado.

Teorema 2: Funções de área constante

Seja \(f\) uma função diferenciável em todo o seu domínio, com \(f'\left ( x \right )\neq 0\), e o triângulo \(\left [ PQR \right ]\) tal como definido no Teorema 1. Então,

\(A_{\Delta}\left ( x \right )=k\) (constante positiva) \(\Leftrightarrow f\left ( x \right )=\pm \frac{k}{x+c}\), com \(c\) constante

Demonstração.

\(\left ( \Leftarrow \right )\) Basta substituir \(f\left ( x \right )\) e \(f'\left ( x \right )\) na expressão \(A\left ( x \right )=\frac{f\left ( x \right )^2}{\left | f'\left ( x \right ) \right |}\) e verificar que tudo se simplifica para \(k\) (é deixado como exercício).

\(\left ( \Rightarrow \right )\) Nesta implicação temos de resolver a equação \(\frac{f\left ( x \right )^2}{\left | f'\left ( x \right ) \right |}=k\) em ordem a \(f\left ( x \right )\) e mostrar que a solução é a família de funções \(f\left ( x \right )=\pm\frac{k}{x+c}\) .

Fazendo \(y=f\left ( x \right )\), a equação (diferencial) fica

\(\frac{y^2}{\left | y' \right |}=k\Leftrightarrow y^2=k\left | y' \right |\Leftrightarrow y^2=-ky'\; \; \; \; \; \left ( y'<0 \right )\vee y^2=ky'\; \; \; \; \; \left ( y'>0 \right )\))

Resolvendo cada uma das equações da disjunção,

\(y^2=-ky'\Leftrightarrow -\frac{y'}{y^2}=\frac{1}{k}\Rightarrow \int -\frac{y'}{y^2}\textrm{d}x=\int \frac{1}{k}\textrm{d}x\Leftrightarrow \frac{1}{y}=\frac{x+c}{k}\Leftrightarrow y=\frac{k}{x+c}\)

\(y^2=ky'\Leftrightarrow \frac{y'}{y^2}=\frac{1}{k}\Rightarrow \int \frac{y'}{y^2}\textrm{d}x=\int \frac{1}{k}\textrm{d}x\Leftrightarrow -\frac{1}{y}=\frac{x+c}{k}\Leftrightarrow y=-\frac{k}{x+c}\)

Isto é,

\(f\left ( x \right )=\pm\frac{k}{x+c}\)

Esta expressão define uma família (infinita) de funções, uma para cada valor da constante real \(c\), de modo que a área do triângulo \(\left [ PQR \right ]\) é sempre \(k\), para cada valor de \(c\).

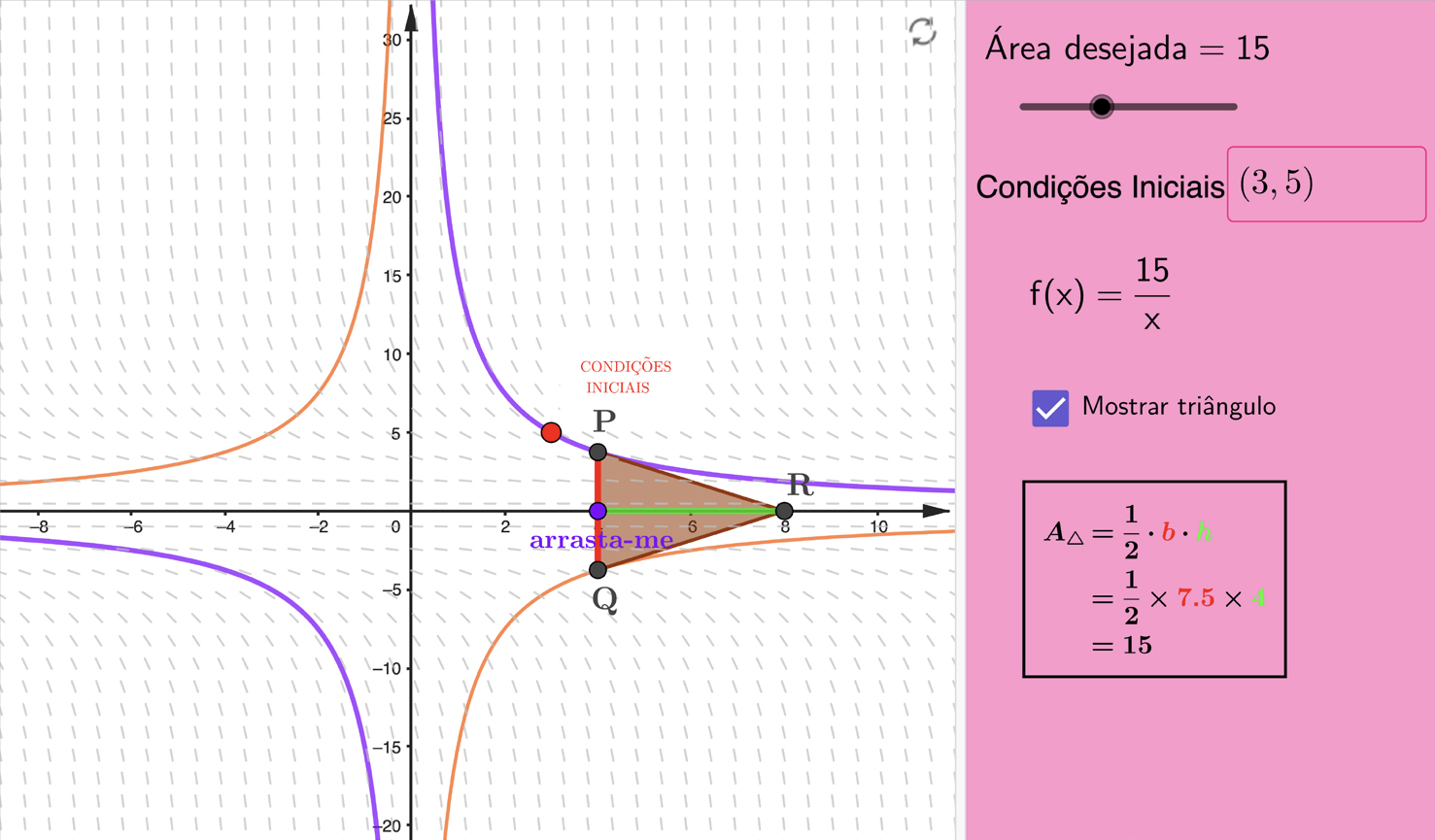
O leitor pode, se entender, manipular a construção GeoGebra aqui, visualizando as curvas integrais da equação diferencial e as soluções para as condições iniciais definidas pelo leitor, assim como o triângulo \(\left [ PQR \right ]\).

No exemplo dado na FIGURA 3, para \(k = 15\) e para a condição \(f\left ( 3 \right )=5\), ou seja, para que \(f\) contenha o ponto (3, 5) e a área do triângulo seja \(15\), \(c = 0\).

Fica como exercício verificar que c pode ser obtido, em função da condição inicial \(f\left ( \alpha \right )=\beta\), pela expressão \(c=\frac{k-\alpha \beta}{\beta}\).

O regresso à simplicidade.

A demonstração do Teorema 2 envolveu a utilização de algum arsenal pesado para um aluno do ensino secundário. Primitivas e integrais definidos é um tópico opcional para o 12.º ano no novo programa (Aprendizagens Essenciais). A demonstração levada a cabo é, de todo o modo, um exemplo de como não devemos usar “bazucas” para resolver problemas de simplicidade conhecida.

Quando se consultam os critérios de classificação deste item, existe uma clara orientação para uma abordagem usando essencialmente ferramentas relacionadas com derivadas de funções e geometria analítica.

A geometria analítica é uma ferramenta muito valiosa que nos foi dada pelos matemáticos do século XVII para resolvermos problemas de geometria (e não só), mas não deve ser vista como uma imposição!

Vejamos uma alternativa de resolução do Problema 16, que deveria estar incluída nos critérios de classificação, e como essa abordagem ao problema permite apresentar uma prova alternativa da implicação \(\left ( \Leftarrow \right )\) do Teorema 2, com alguns recursos de geometria sintética que, em última instância, derivam de propriedades da hipérbole.

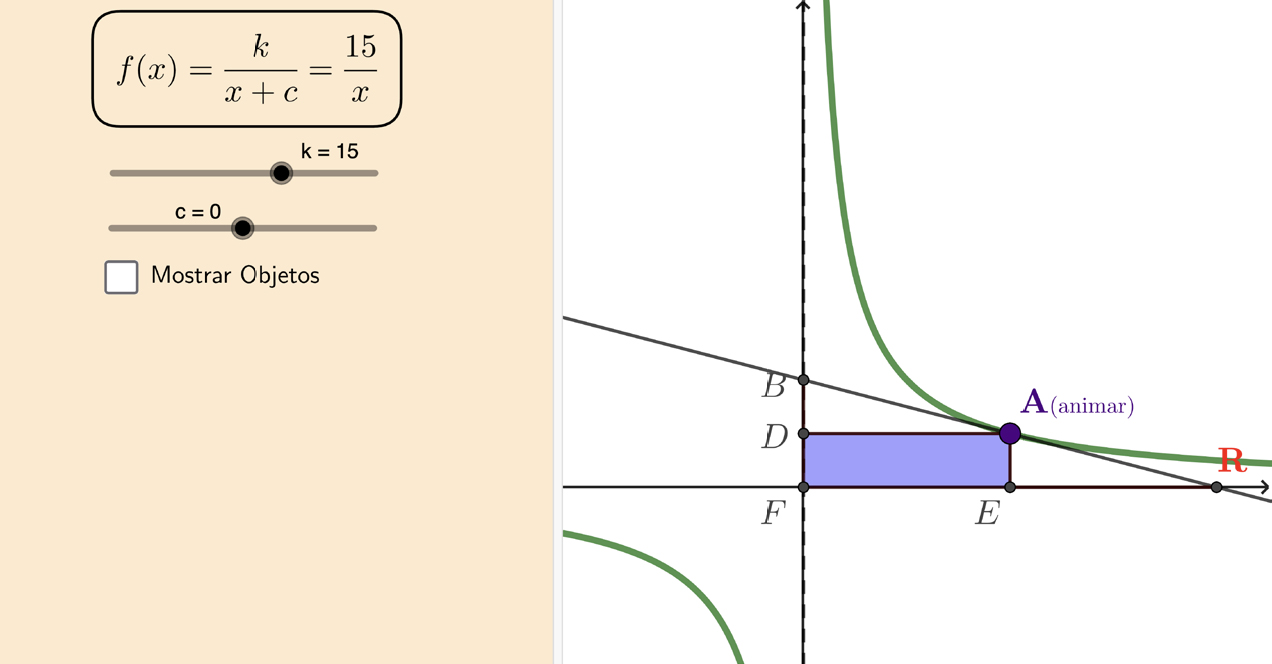
Partamos da situação mais simples, exatamente a função do Problema 16, \(f\left ( x \right )=\frac{k}{x}\). Esta é a conhecida função de proporcionalidade inversa de constante \(k\), já muito familiar no ensino básico (9.º ano). Também se pode escrever \(xy = k\). O significado geométrico desta expressão é óbvio, muito explorado no 9.º ano: a área do quadrilátero \(\left [ FEAD \right ]\), de dimensões \(x=\overline{FE}\) e \(y=\overline{AD}\) é constante e igual a \(k\) (ver FIGURA 5).

O declive da reta tangente em \(A\left ( x,\frac{k}{x} \right )\) é \(-\frac{k}{x^2}=f'\left ( x \right )\). O declive da reta \(ED\) também é \(-\frac{k}{x^2}\) (porquê?). Assim, as retas \(RB\) e \(ED\) são paralelas e \(\overline{BD}=\overline{AE}\) e \(\overline{DA}=\overline{ER}\), uma vez que \(\left [BDEA\right ]\) e \(\left [DERA\right ]\) são paralelogramos. Assim, a área do retângulo \(\left [FEAD\right ]\) é igual à soma das áreas dos triângulos \(\left [BDA\right ]\) e \(\left [ERA\right ]\), ou seja, o triângulo \(\left [FRB\right ]\) pode sempre ser decomposto em quatro triângulos equivalentes (independentemente da localização do ponto \(A\) no gráfico de \(f\left ( x \right )=\frac{k}{x}\)). Por aqui fica arrumado o Problema 16 pois basta fazer uma simetria do triângulo \(\left [ERA\right ]\) relativamente ao eixo \(Ox\) e obtemos o triângulo \(\left [ AA'R \right ]\)  (\(\left [ PQR \right ]\) no problema) com área igual a \(k\). O ponto \(A′\), simétrico de \(A\) em relação ao eixo \(Ox\), fica sobre o gráfico da função \(g = −f\). Fica aqui a proposta de manipular a construção GeoGebra, ou clicando sobre a FIGURA 5, onde se pode observar os argumentos atrás apresentados.

Quando passamos para funções do tipo \(h\left ( x \right )=\pm\frac{k}{x+c}=\pm f\left ( x+c \right ),c\in\mathbb{R}\), as áreas são totalmente preservadas pois as únicas transformações do gráfico de \(f\) são a translação e a simetria em relação a eixo \(Ox\) (10.º ano). Logo, tudo o que foi provado para \(f\left ( x \right )=\frac{k}{x}\) fica provado para \(h\left ( x \right )=\pm\frac{k}{x+c}\), tendo em consideração que a assímptota \(x = −c\) faz o papel de eixo \(Oy\) em toda a construção geométrica descrita.

Assim, \(f\left ( x \right )=\pm \frac{k}{x+c}\; _{\textrm{definicao}}{\Rightarrow }A_{\left [ FEAD \right ]}=k\; _{\textrm{Prop. geometricas}}{\Rightarrow }A_{\textrm{AA'R}}=k\).