As colisões que conservam a energia cinética são ditas elásticas e, quando ocorre variação de energia cinética, são ditas inelásticas. Nas colisões perfeitamente inelásticas, os corpos seguem juntos, resultando na maior perda possível de energia cinética do sistema. Se são dadas as massas, as velocidades e ângulos iniciais e as colisões são elásticas ou perfeitamente inelásticas, então existe solução analítica para as velocidades finais dos dois corpos. Nos casos intermédios, é necessária mais informação, como um ângulo de deflexão ou o coeficiente de restituição. Na literatura, geralmente, não é abordado mais nenhum caso para o qual baste conhecer as condições iniciais para conhecer as finais. Aqui, apresentamos outro: a colisão de corpos plásticos, corpos que não restituem a sua forma nem coalescem.

Vamos considerar colisões de anéis, discos ou esferas quando existem apenas forças radiais repulsivas resultantes da deformação dos corpos. Supomos ausência de qualquer outra força na superfície de contacto, nomeadamente, força de atrito ou de algum tipo de ligação. Os resultados são obtidos para o limite em que o tempo de colisão tende a zero ou, de forma similar, para o limite de rigidez infinita dos corpos. Numa colisão oblíqua (desalinhada), forças radiais resultantes da deformação não permitem que os corpos sigam juntos. Para este tipo de interação, mostraremos que a máxima dissipação de energia cinética ocorre para impulsos com metade da intensidade dos impulsos que correspondem a uma colisão elástica. Assim, é possível calcular as velocidades finais dos corpos. Este é um caso que não encontramos em literatura comummente usada neste nível de estudo. Também veremos que a máxima dissipação de energia com impulsos radiais é coerente com uma deformação plástica.

Equações da colisão com forças radiais repulsivas.

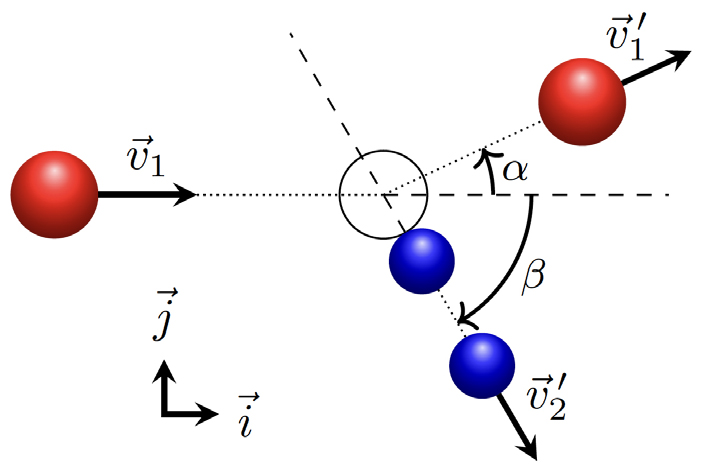
Na ausência de forças exteriores (ou quando estas se anulam), o momento linear de um sistema conserva-se e a variação da energia cinética não depende do referencial. Escolhemos o referencial do laboratório, veja a FIGURA 1, como sendo aquele em que um corpo se move para a direita (o corpo 1) e colide com outro que está parado (o corpo 2). Escreveremos as coordenadas de todos os vetores na base \(\left ( \vec{i},\vec{j} \right )\). As velocidades iniciais dos corpos 1 e 2 no referencial do laboratório são

\(\vec{v}_1=\left ( \left | \vec{v}_1 \right |,0 \right )\; \; \; \; \; \vec{v}_2=\left ( 0,0 \right )\) (1)

Para as velocidades finais, usamos a mesma notação de Alonso e Finn, o apóstrofo; para os módulos das velocidades, usaremos a notação \(\left | \vec{v} \right |=v\). Sendo \(\alpha\) e \(\beta\) os ângulos de deflexão, as velocidades finais são

\(\vec{v}_1=v_{1}^{'}\left ( \cos\left ( \alpha \right ),\textrm{sen}\left ( \alpha \right ) \right ),\; \; \; \; \; \vec{v}_2=v_{2}^{'}\left ( \cos\left ( \beta \right ),-\textrm{sen}\left ( \beta \right ) \right )\) (2)

Supomos que a interação entre os corpos resulta apenas de deformações infinitesimais do material, excluímos forças de atrito ou ligação. No limite de rigidez infinita, a geometria dos corpos permanece inalterada, pelo que os impulsos são radiais, repulsores e não produzem rotação, ver FIGURA 2.

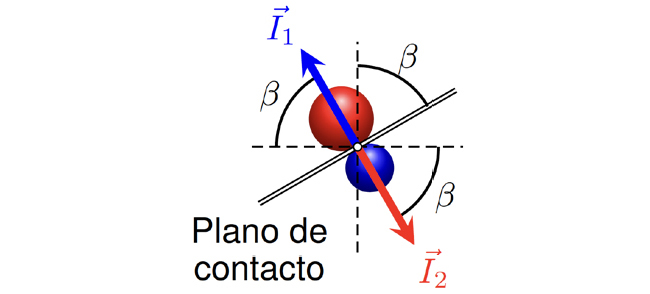
O plano tangente ao ponto de contacto entre os corpos será referido como plano de contacto. Assim, os impulsos serão perpendiculares ao plano de contacto, fazendo este plano um ângulo \(\beta\) com a vertical — este \(\beta\) é o mesmo da eq. (2), como veremos. As forças de contacto formam pares ação–reação, resultando na conservação do momento linear do sistema. Sendo \(\vec{I}_1\) o impulso no corpo 1 e \(\vec{I}_2\) o impulso no corpo 2, temos \(\vec{I}_1=-\vec{I}_2\). Sendo \(I\) a intensidade destes dois impulsos, podemos escrever

\(\vec{I}_1=I\left ( -\cos\left ( \beta \right ),\textrm{sen}\left ( \beta \right ) \right ),\; \; \; \; \; \vec{I}_2=I\left ( \cos\left ( \beta \right ),-\textrm{sen}\left ( \beta \right ) \right )\) (3)

onde \(\beta\in \left [ 0^{\circ},90^{\circ} \right [\); excluímos o caso limite do plano de contacto horizontal.

Sendo o impulso igual à variação do momento linear, temos

\(\vec{I}_1=m_1\vec{v}_{1}^{'}-m_1\vec{v}_1,\; \; \; \; \; \vec{I}_2=m_2\vec{v}_{2}^{'}-m_2\vec{v}_2\) (4)

De (1), (3) e (4), obtemos as velocidades finais

\(\vec{v}_{1}^{'}=\left ( v_1-\frac{I}{m_1}\cos\left ( \beta \right ),\frac{I}{m_1}\textrm{sen}\left ( \beta \right ) \right )\; \; \; \; \; \vec{v}_{2}^{'}=\left ( \frac{I}{m_2}\cos\left ( \beta \right ),-\frac{I}{m_2}\textrm{sen}\left ( \beta \right ) \right )\) (5)

Como o corpo 2 parte do repouso, a sua velocidade final tem a mesma direção e sentido do impulso que recebe, \(\vec{I}_2\) — por isso, o ângulo de deflexão, \(\beta\) da eq. (2), e ângulo do plano de contacto são iguais.

O dobro da dissipação de energia cinética, \(K\), é dada por

\(2\Delta K=m_1\left | \vec{v}_1 \right |^2+m_2\left | \vec{v}_2 \right |^2-m_1\left | \vec{v}_{1}^{'} \right |^2-m_2\left | \vec{v}_{2}^{'} \right |^2\)

\(=-m_1\left ( \frac{I}{m_1} \right )^2+2m_1v_1\frac{I}{m_1}\cos\left ( \beta \right )-m_2\left ( \frac{I}{m_2} \right )^2\) (6)

\(=2v_1I\cos\left ( \beta \right )-\frac{m_1+m_2}{m_1m_2}I^2\)

Mantendo fixos \(v_1\) e \(\beta\), a conservação de energia, \(\Delta K = 0\), é obtida com o impulso

\(I_e=2\frac{m_1m_2}{m_1+m_2}v_1\cos\left ( \beta \right )\) (7)

Usamos o índice “\(e\)” para indicar colisão elástica. Derivando (6) em ordem a \(I\), obtemos

\(\frac{d}{dI}\left ( 2\Delta K \right )=2v_1\cos\left ( \beta \right )-2\frac{m_1+m_2}{m_1m_2}I\)

\(\frac{d^2}{dI^2}\left ( 2\Delta K \right )=-2\frac{m_1+m_2}{m_1m_2}<\)\(0\)

logo, a máxima dissipação é obtida para o impulso

\(I_p=\frac{m_1m_2}{m_1+m_2}v_1\cos\left ( \beta \right )\) (8)

As colisões de impulso radial máximo-dissipativas são compatíveis com um material que não restitui a sua forma, um material plástico. Assim, estas colisões serão referidas como “plásticas” e usaremos o índice “\(p\)”.

A característica do material, elástico ou plástico, determina o tipo de colisão. Fixo o tipo de colisão, são o desalinhamento geométrico da colisão — aqui medido pelo ângulo \(\beta\) —, a velocidade e as massas que determinam o impulso. De (7) e (8), sabemos que ambos os impulsos diminuem com o ângulo \(\beta\), o que está de acordo com a intuição “quanto mais de raspão, menor o impacto”.

Da comparação entre (7) e (8), concluímos que

A intensidade do impulso numa colisão plástica é metade da intensidade do impulso numa colisão elástica.

Fizeram-se experiências para colisões frontais \(\left ( \beta=0 \right )\) congruentes com esta afirmação. Não foram feitas experiências para colisões oblíquas \(\left ( \beta\neq0 \right )\) que permitam avaliar a afirmação nos casos de maior interesse.

Colisão conservativa (elástica).

As colisões elásticas (conservativas) são muito estudadas. Ainda assim, apresentamos vários resultados. De (5) e (7), obtemos as velocidades finais no referencial do laboratório,

\(\vec{v}_{1e}^{'}=v_1\left ( 1-2\frac{m_2}{m_1+m_2}\cos^2\left ( \beta \right ),2\frac{m_2}{m_1+m_2}\cos\left ( \beta \right )\textrm{sen}\left ( \beta \right ) \right )\) (9a)

\(\vec{v}_{2e}^{'}=v_1\left ( 2\frac{m_1}{m_1+m_2}\cos^2\left ( \beta \right ),-2\frac{m_1}{m_1+m_2}\cos\left ( \beta \right )\textrm{sen}\left ( \beta \right ) \right )\) (9b)

O produto escalar das velocidades (9a) e (9b) é

\(\vec{v}_{1e}^{'}\cdot\vec{v}_{2e}^{'}=2\frac{m_1}{m_1+m_2}\left ( \frac{m_1-m_2}{m_1+m_2} \right )v_{1}^{2}\cos^2\left ( \beta \right )=v_{1e}^{'}\cdot v_{2e}^{'}\cdot \cos\left ( \alpha+\beta \right )\) (10)

De (10), obtém-se o conhecido resultado para colisões elásticas:

• \(\alpha+\beta >90^{\circ}\), se \(m_1 <\)\(m_2\);
• \(\alpha+\beta =90^{\circ}\), se \(m_1=m_2\);
• \(\alpha+\beta <\)\(90^{\circ}\), se \(m_1>m_2\);

Para \(\beta=0\) e \(m_1 = m_2\), temos \(\vec{v}_{1}^{'}=\vec{0}\); apesar de o vetor nulo não definir qualquer ângulo de deflexão \(\alpha\), podemos considerar \(\alpha=90^{\circ}\), mantendo-se assim válida a soma \(\alpha+\beta=90^{\circ}\) no caso \(m_1 = m_2\). Note que, se \(\beta= 0\), temos \(\alpha= 0\) para \(m_1 > m_2\) e \(\alpha=180^{\circ}\) para \(m_1 <\)\( m_2\); então, a escolha \(\alpha=90^{\circ}\) para \(m_1 = m_2\) é aceitável também aqui.

Numa colisão elástica com massas idênticas, \(m_1 = m_2 = m\), as velocidades (9a) e (9b) são

\(\vec{v}_{1e}^{'}=v_1\textrm{sen}\left ( \beta \right )\left ( \textrm{sen}\left ( \beta \right ),\cos\left ( \beta \right ) \right ),\; \; \; \; \; \vec{v}_{2e}^{'}=v_1\textrm{cos}\left ( \beta \right )\left ( \textrm{cos}\left ( \beta \right ),-\textrm{sen}\left ( \beta \right ) \right )\)

de onde concluímos que

\(\left ( i \right )\left | \vec{v}_{1e}^{'} \right |=v_1\textrm{sen}\left ( \beta \right ),\; \; \; \; \; \left ( ii \right )\left | \vec{v}_{2e}^{'} \right |=v_1\cos\left ( \beta \right )\)

\(\left ( i \right )\alpha_e=90^{\circ}-\beta,\; \; \; \; \; \left ( ii \right )K_{e}^{'}=K\)

onde \(K=\frac{1}{2}mv_{1}^{2}\) é a energia cinética inicial no referencial do laboratório.

Deixamos ao leitor o estudo das velocidades no referencial do centro de massa, referencial onde se pode mostrar que os corpos se comportam como se colidissem elasticamente contra uma parede cuja superfície é o plano de contacto, ver FIGURA 3A), onde apresentamos uma colisão elástica não instantânea com uma superfície horizontal.

Colisão máximo-dissipativa (plástica).

Como vimos, a colisão máximo-dissipativa ocorre para impulsos dados pela eq. (8). Substituindo (8) em (5), obtemos as velocidades finais para uma colisão plástica

\(\vec{v}_{1p}^{'}=v_1\left ( 1-\frac{m_2}{m_1+m_2}\cos^2\left ( \beta \right ),\frac{m_2}{m_1+m_2}\cos\left ( \beta \right )\textrm{sen}\left ( \beta \right ) \right )\) (11a)

\(\vec{v}_{2p}^{'}=v_1\left ( \frac{m_1}{m_1+m_2}\cos^2\left ( \beta \right ),-\frac{m_1}{m_1+m_2}\cos\left ( \beta \right )\textrm{sen}\left ( \beta \right ) \right )\) (11b)

O produto interno das velocidades finais, (11a) e (11b), é

\(\vec{v}_{1p}^{'}\cdot\vec{v}_{2p}^{'}=\vec{v}_{1}^{2}\left ( \frac{m_1}{m_1+m_2} \right )^2\cos^2\left ( \beta \right )=\vec{v}_{1p}^{'}\cdot\vec{v}_{2p}^{'}\cdot \cos\left ( \alpha+\beta \right )\) (14)

Dado (14), qualquer que seja a proporção entre as massas, nas colisões plásticas temos:

\(\alpha+\beta<\)\(90^{\circ}\)

Para uma colisão plástica com massas idênticas, \(m_1 = m_2 = m\), as velocidades (11a) e (11b) são

\(\vec{v}_{1p}^{'}=\frac{1}{2}v_1\left ( 1+\textrm{sen}^2\left ( \beta \right ),\cos\left ( \beta \right )\textrm{sen}\left ( \beta \right ) \right )\),

\(\vec{v}_{2p}^{'}=\frac{1}{2}v_1\cos\left ( \beta \right )\left ( \cos\left ( \beta \right ),-\textrm{sen}\left ( \beta \right ) \right )\)

Assim, no caso plástico, temos

\(\left ( i \right )v_{1p}^{'}=\frac{1}{2}v_1\sqrt{1+3\textrm{sen}^2\left ( \beta \right )},\; \; \; \; \; \left ( ii \right )v_{2p}^{'}=\frac{1}{2}v_1\cos\left ( \beta \right )\),

\(\left ( i \right )\tan\left ( \alpha_p \right )=\frac{\cos\left ( \beta \right )\textrm{sen}\left ( \beta \right )}{1+\textrm{sen}^2\left ( \beta \right )},\; \; \; \; \; \left ( ii \right )K_{p}^{'}=\frac{1}{2}\left ( 1+\textrm{sen}^2\left ( \beta \right ) \right )K\)

Pode mostrar-se, no referencial do centro de massa, que os corpos se comportam como se colidissem contra uma parede plana sem atrito, cuja superfície é o plano de contacto, perdendo toda a componente da velocidade normal ao plano, veja a FIGURA 3B).

Deformações elásticas e plásticas.

A deformação de um corpo pode ser modelada por dois casos limite.

• Deformação elástica: a forma do corpo é totalmente restituída; deforma durante a compressão e recupera a forma na expansão; toda a energia absorvida durante a compressão é libertada na expansão (como se fosse uma mola perfeita).
• Deformação plástica: a deformação é irreversível; deforma durante a compressão e não apresenta a fase de expansão; toda a energia absorvida durante a compressão transforma- se em energia interna.

Na FIGURA 3, apresentamos a colisão não instantânea entre corpos com uma superfície sem atrito, pelo que os corpos deslizam livremente sobre a mesma — não rodam e as componentes das velocidades tangenciais ao plano são mantidas. Na colisão elástica, FIGURA 3A), a componente normal da velocidade é anulada durante a fase de deformação, depois, inverte-se durante a fase de expansão. Toda a energia cinética é restituída. Na colisão plástica, FIGURA 3B), a componente normal da velocidade também é anulada durante a fase de deformação, contudo, não existe fase de expansão. Assim, nem a forma do corpo, nem a energia cinética são restituídas.

Para deformações infinitesimais, estas descrições são idênticas às das colisões conservativas e máximo-dissipativas, razão pela qual usamos os adjetivos elástico e plástico para essas colisões.