1. Leis de Kepler.

No princípio do século XVII, Johann Kepler (1571-1630), a partir de uma grande quantidade de observações astronómicas efectuadas por Tycho Brahe (1546-1601), nos últimos 20 anos da sua vida, formulou as seguintes três leis para o movimento dos planetas em torno do Sol:

• Primeira Lei de Kepler (Lei das elipses). “Cada planeta move-se sobre uma elipse com o sol num dos focos”.
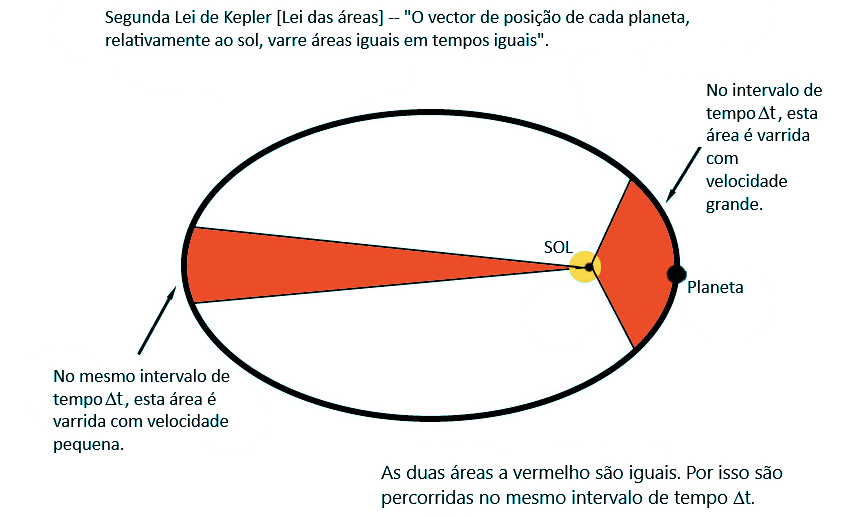
• Segunda Lei de Kepler (Lei das áreas). “O vetor de posição de cada planeta, relativamente ao sol, varre áreas iguais em tempos iguais” (FIGURA 2).
• Terceira Lei de Kepler (Lei dos períodos). “O quadrado do período (i.e., o tempo necessário para completar uma órbita), é proporcional ao cubo do eixo maior da elipse, sendo a constante de proporcionalidade a mesma para todos os planetas”.

Poucos contestaram a segunda e terceira leis. Resultavam de observações e só restava fazer os cálculos para as confirmar. Mas a primeira lei causou muita perturbação para quem estava habituado a pensar só em retas e círculos! Porquê uma elipse? Porque é que os céus, numa manifestação pura da vontade divina, optava por uma forma distorcida de uma figura perfeita - o círculo?

Isaac Newton, na sua obra monumental, intitulada Philosophiae Naturalis Principia Mathematica, estabeleceu os fundamentos da chamada mecânica clássica (ou Newtoniana), que ainda hoje se aprende nos cursos iniciais de Física.

Nessa obra genial, publicada em 1687, Newton confirmou o modelo de Kepler, e restaurou a sua pureza, ao mostrar que as órbitas elípticas, como previstas pelas leis de Kepler, são na realidade equivalentes ao facto de que a aceleração gravitacional é inversamente proporcional ao quadrado da distância ao corpo em órbita. Veremos tudo isto em detalhe daqui a pouco!

Newton começa por definir massa, momento (a que chama movimento = massa × velocidade), vários tipos de forças e aceleração, e formula então 3 axiomas ou Leis de movimento que vão ser o pilar da sua Mecânica Clássica (Newtoniana).

2. Leis de Newton.

• 1.ª Lei de Newton (Lei de inércia). “Um corpo em repouso permanecerá sempre em repouso e um corpo em movimento retilíneo uniforme (com velocidade constante), assim continuará, a não ser que, em ambos os casos, sobre ele actue uma força exterior”.
• 2.ª Lei de Newton. “A aceleração de um corpo é proporcional à força que sobre ele atua e está dirigida segundo a direção dessa força”:

\(\textbf{F}=m\textbf{a}\) (1)

• 3.ª Lei de Newton (Lei da ação-reação). “A toda a ação, de um corpo sobre outro, corresponde uma reação igual e oposta, exercida pelo segundo corpo sobre o primeiro.”.

Cerca de 50 anos mais tarde, Isaac Newton (1642-1727) utilizou a sua própria lei: “Força = massa × aceleração” para deduzir, a partir das leis de Kepler, a natureza básica da força que mantém cada planeta na respectiva órbita.

3. Método da aproximação poligonal de Newton.

Newton trabalha sempre com pequenas forças instantâneas que provocam mudanças discretas na velocidade, e portanto nas trajetórias, dos corpos onde actuam. Só posteriormente, com o génio da concepção do cálculo, apercebe-se que as mudanças contínuas podem ser aproximadas por, e são de facto, o “limite” das mudanças discretas.

Em 1687 Newton usou um método da aproximação poligonal para demonstrar a lei das áreas de Kepler, válida para qualquer força central. Expliquemos melhor o seu argumento. Um corpo de massa 1 desloca-se da posição inicial \(P_0\) até à posição \(P_1\), com movimento retílineo uniforme com velocidade \(V_0\), durante um intervalo de tempo \(\Delta t\). Portanto, a distância que ele percorre, ao ir da posição \(P_0\) até à posição \(P_1\), é igual a:

\(\left| P_0P_1\right|=v_0\times \Delta t,\; \; \; \; \; v_0=\left\| V_0\right\|\)

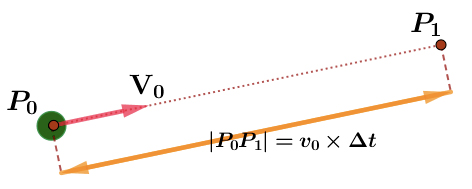
Na posição \(P_1\), o corpo é sujeito à ação de uma força impulsiva \(F\) (uma “pancada”!), dirigida para o centro de forças fixo \(S\). A força atua durante um intervalo de tempo muito pequeno \(\delta t\)t, comunicando pois ao corpo uma velocidade:

\(W_1=F\delta t\)

(não esqueça que estamos a supôr que a massa do corpo é igual a 1).

Se o corpo estivesse em repouso na posição \(P_1\), ele deslocar-se-ia na direção de \(W_1\), percorrendo uma distância igual a \(w_1 × \Delta t\), ao fim do intervalo de tempo \(\Delta t\).

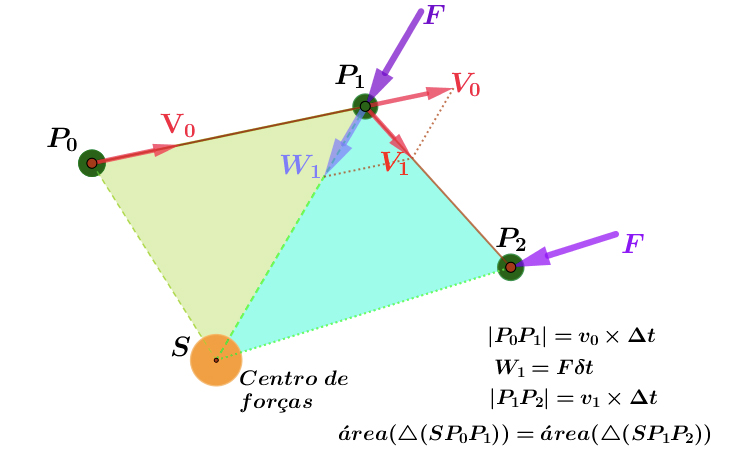
Por outro lado, se a força \(F\) não existisse, o corpo deslocar-se-ia por inércia na direção de \(V_0\), percorrendo, a partir da posição \(P_1\), uma distância igual a \(v_0 × \Delta t\), ao fim do mesmo intervalo de tempo \(\Delta t\).

Mas agora, na posição \(P_1\), o corpo está sujeito à lei de composição de velocidades. Pela regra do paralelogramo, a velocidade que ele adquire será:

\(V_1 = V_0 +W_1\)

e, ao fim do mesmo intervalo de tempo \(\Delta t\), ele atinge a posição \(P_2\), na direção de \(V_1\), tal que:

\(\left| P_1P_2\right|=v_1\times \Delta t\)

Em \(P_2\), o corpo sofre uma nova “pancada”, \(F\), dirigida para o centro de forças fixo \(S\), e o processo repete-se (FIGURA 15).

Este método é consecutivamente usado por Newton em toda a sua Dinâmica.

Teorema (Newton Proposição I).

Seja \(S\) um ponto fixo (o Sol) e \(P\) um ponto móvel (um planeta) sobre o qual, em cada instante, a única força, \(F\), que nele atua é central, isto é, tem a direção de \(P\) para \(S\). Então:

• A trajetória de \(P\) é plana.
• O segmento \(SP\) varre áreas iguais em intervalos de tempo iguais.

Nota.

Note que isto afirma muito mais do que a 1.ª lei de Kepler! De facto, áreas iguais em intervalos de tempo iguais é consequência de qualquer força radial \(F\), independentemente da forma como ela varia em intensidade!

Demonstração.

É claro que o teorema é verdadeiro quando não há forças a actuar em \(P\) - neste caso, a 1.ª lei de Newton diz que \(P\) tem movimento retilíneo uniforme (com velocidade constante). Isto implica que \(P\) percorre distâncias iguais, em intervalos de tempo iguais, sobre a sua trajetória retilínea \(l\). Podemos supôr, é claro, que \( S\in l\). Caso contrário SP varre área nula.

Fixemos um certo intervalo de tempo \(\Delta t > 0\). Suponhamos que \(P\) parte de \(P_0\), com velocidade constante \(V_0\), e atinge \(P_1\) ao fim do tempo \(\Delta t\). Portanto:

\(P_1 = P_0 + V_0\Delta t \rightarrow\) distância \((P_0, P_1) = v_0\Delta t\)

onde \(v_0=\left\| V_0\right\|\).

Suponhamos agora que o planeta \(P\), quando atinge o ponto \(P_1\), é atuado por uma força instantânea \(F\), radial – dirigida segundo a reta \(P_1S\) (FIGURA 6). A 2.ª lei de Newton diz-nos que isto faz surgir uma nova componente para a velocidade \(W_1 = F\delta t\), de \(P\), em \(P_1\), dirigida segundo a reta \(P_1S\). Note que \(W_1\) pode apontar para S ou no sentido oposto. Por outras palavras, a força força instantânea \(F\) pode empurrrar \(P\) em direção a \(S\) (força atrativa) ou afastar \(P\) de \(S\) (força repulsiva). Na FIGURA 6 ela é atrativa.

Se \(F = 0\), isto é, se não existisse a força \(F\), \(P\) seguiria por inércia a sua trajetória retílinea, com a mesma velocidade \(V_0\), atingindo um ponto \(Q\), ao fim do tempo \(\Delta t\).

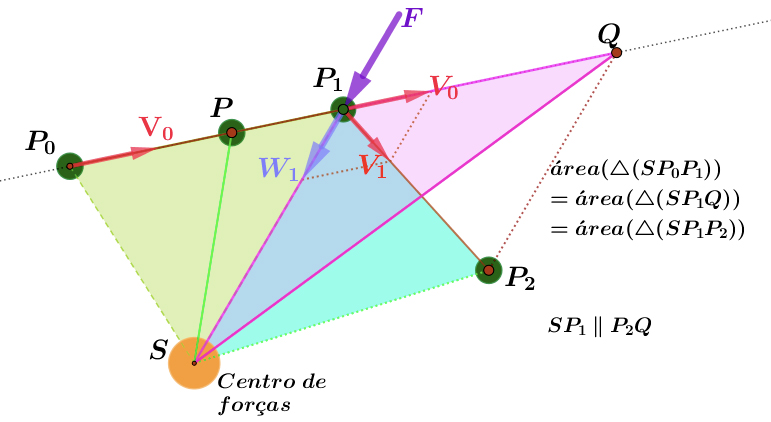
Mas quando \(F\neq 0\), a velocidade resultante, \(V_1\) é obtida pela regra do paralelogramo:

\(V_1 = V_0 +W_1\)

e o planeta \(P\) segue agora uma outra trajetória retilínea, atingindo um ponto \(P_2\), ao fim do tempo \(\Delta t\):

\(P_2 = P_1 + V_1\Delta t \rightarrow\) distância \((P_1, P_2) = v_1\Delta t\)

onde \(v_1=\left\| V_1\right\|\). Como \(P_2\) está no plano definido por \(S\), \(P_0\) e por \(P_1\), o movimento é plano.

A área varrida por \(PS\), quando agora \(P\) vai de \(P_1\) a \(P_2\), é a área do \(\Delta (SP_1P_2)\). Mas esta é também a área do triângulo \(\Delta (SP_1Q)\), uma vez que eles têm a mesma base, o segmento \(P_1S\), e a mesma altura, já que a reta \(QP_2\) é paralela à reta \(P_1S\). Portanto:

área \((\Delta (SP_0P_1))\) = área \((\Delta (SP_1Q))\) = área \((\Delta (SP_1P_2))\)

e o teorema está demonstrado.

*

4. A Proposição XI dos Principia Mathematica de Newton.

Hoje em dia é mais usual deduzir a 2.ª lei de Kepler – órbitas elípticas - a partir da lei da atração universal de Newton - força inversamente proporcional ao quadrado da distância entre os dois corpos.

No entanto, Newton não procedeu desta forma. De facto, nos seus Principia Mathematica, começou por testar outras possibilidades para a força de atração. Só depois destas tentativas, ele deduz a sua lei da atração universal. Como? Em primeiro lugar, assume como verdadeiras as duas primeiras leis de Kepler e, em segundo lugar, usa argumentos muito engenhosos, baseados essencialmente em geometria de cónicas, em grande parte criada por Apolónio de Perga (262-170 a.C.), que Newton conhecia.

Vale a pena descrever as linhas gerais do argumento de Newton.

Teorema (Newton Proposição XI).

Suponhamos que \(P\) se move numa elipse \(\varepsilon \) e que a aceleração de \(P\) é sempre radial, isto é, tem sempre a direção de \(P\) para \(S\), onde \(S\) é um foco da elipse \(\varepsilon \).

Então a intensidade dessa aceleração, e portanto da força radial atrativa que atua em \(P\), é inversamente proporcional ao quadrado da distância entre \(P\) e \(S\).

Suponhamos que o planeta \(P\) se move ao longo da trajetória \(P (t)\), sob a ação de uma força central, de centro \(S\) (o Sol). Seja \(F (P (t))\) a força que atua no corpo quando este ocupa a posição \(P (t)\).

Qual a relação entre a grandeza da força \(F (P (t)) = \left\| F (P (t))\right\|\) e a forma geométrica da trajetória do corpo?

Analisemos o raciocínio (genial) de Newton, para responder a esta pergunta.

Seja \(\Delta t\) um pequeno intervalo de tempo e suponha que o corpo se move de \(P\) até \(Q\) nesse intervalo de tempo. Neste percurso a força central que atua no corpo não varia muito e podemos supôr que é constante e igual a \(F (P)\) – o valor que tem em \(P\) – tal como Newton o fez. Consideremos a tangente à órbita no ponto \(P\).

Newton imagina que o percurso de \(P\) a \(Q\) é composto por dois movimentos (FIGURA 7):

• Movimento retilíneo uniforme de \(P\) a \(R\), situado sobre a tangente referida. De facto, se o corpo não fosse sujeito à ação da força \(F (P)\), ele deslocar-se-ia por inércia, com velocidade uniforme \(V\), igual à que tem em \(P\). Este movimento tem pois aceleração nula.
• Movimento retilíneo de \(R\) a \(Q\) com uma direção paralela a \(PS\), com velocidade inicial nula, movimento esse provocado pela “pancada” que o corpo sofre, quando “percurtido” pela força central \(F (Q) \approx F (Q)\), que o obriga a deslocar-se na direção de \(S\). Esta componente do movimento tem aceleração inteiramente determinada pela força central.

Quando o corpo se desloca de \(P\) para \(Q\) estes dois movimentos ocorrem em simultâneo. Mas, ao decompor o trajeto de \(P\) para \(Q\) nas duas partes separadas acima descritas, Newton foi capaz de isolar o efeito da força central e progredir na sua análise. Vejamos como.

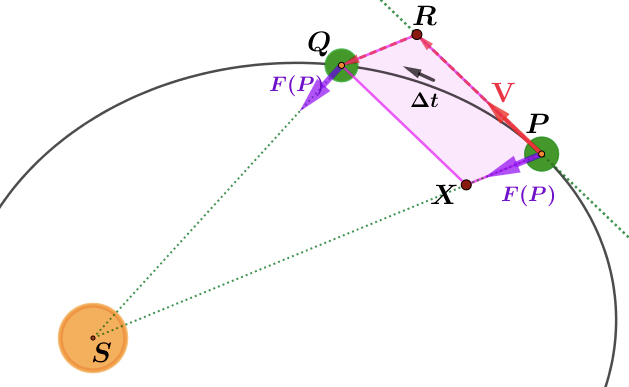
Suponha que o corpo tem massa m (Kg por exemplo). Como Força = massa × aceleração, a força \(F (P)\) (suposta constante no percurso de \(P\) a \(Q\), como acima se referiu), produz uma aceleração constante igual a \(\frac{1}{m}F\left ( P \right )\), durante o intervalo \(\Delta t\), correspondente ao movimento de \(R\) a \(Q\).

Como se sabe, um corpo que, partindo do repouso, se move com aceleração constante \(a=\frac{1}{m}F\left ( P \right )\), tem no instante t uma velocidade igual a:

\(V\left ( t \right )=at+V\left ( 0 \right )=\frac{1}{m}F\left ( P \right )t+0=\frac{1}{m}F\left ( P \right )t\)

e percorre uma distância igual a:

\(d\left ( t \right )-d\left ( 0 \right )=\frac{a}{2}t^{2}=\frac{1}{2m}F\left ( P \right )t^{2}\)

Concluindo.

A força \(F (P)\) produz um deslocamento igual a \(\frac{1}{2m}F\left ( P \right )\left ( \Delta t \right )^{2}\), no intervalo de tempo \(\Delta t\). Isto é, \(\frac{1}{2m}F\left ( P \right )\left ( \Delta t \right )^{2}=\left| QR\right|\). Newton determina portanto que:

\(F\left ( P \right )=2m\frac{\left| QR\right|}{\left ( \Delta t \right )^{2}}\) (2)

Newton completa agora a FIGURA 7, para incluir a informação da lei das áreas de Kepler.

Observe a FIGURA 8. Como \(\Delta t\) é muito pequeno, e portanto \(Q\) está muito próximo de \(P\), a área do setor \(SPQ\) é quase igual à área do triângulo \(\Delta (SPQ)\), que é, por sua vez, igual a \(\frac{1}{2}\left ( \left| SP\right|\times \left| QT\right| \right )\). Como \(\overrightarrow{SP}\) varre a área do setor \(SPQ\) no intervalo de tempo \(\Delta t\), segue- se que:

\(\frac{\frac{1}{2}\left ( \left| SP\right|\times \left| QT\right| \right )}{\Delta t}=\frac{\mathrm{area \; do \; setor\; }SPQ}{\Delta t}\equiv \kappa\)

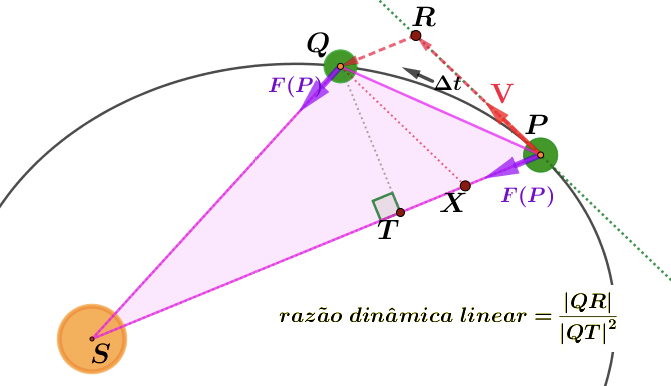
onde \(\kappa\) é uma constante – a chamada a constante de Kepler da órbita. O seu significado é o seguinte: \(\kappa\) é a velocidade areolar (área/unidade de tempo), com que a área é varrida pelo vetor de posição \(\overrightarrow{SP}\), à medida que \(P\) se desloca sobre a sua órbita, sob a ação da força central \(F\). Pela lei das áreas esta velocidade é constante.

Portanto \(\Delta t=\frac{2\kappa}{\left| SP\right|\times \left| QT\right|}\) e substituindo em (2) vem que:

\(F\left ( P \right )=\frac{8\kappa^{2}m}{\left| SP\right|^{2}}\frac{\left| QR\right|}{\left| QT\right|^{2}}\) (3)

Como a área do setor \(SPQ\) é apenas aproximadamente igual à área do triângulo \(\Delta (SPQ)\), esta é uma expressão aproximada da grandeza \(F (P)\) da força. Contudo esta aproximação melhora à medida que \(\Delta t \rightarrow 0\), isto é, à medida que \(Q \rightarrow P\). Como \(\kappa\) e \(m\) são constantes e \(\left| SP\right|\) é a distância de \(P\) a \(S\), concluímos que \(\frac{8\kappa^{2}m}{\left| SP\right|^{2}}\) não depende de \(Q\) e portanto:

\(F\left ( P \right )=\frac{8\kappa^{2}m}{\left| SP\right|^{2}}\displaystyle \lim_{Q \to P}\frac{\left| QR\right|}{\left| QT\right|^{2}}\) (4)

Newton chamou ao quociente \(\frac{\left| QR\right|}{\left| QT\right|^{2}}\) a razão dinâmica linear. O cálculo da força consiste pois em analisar em detalhe qual o limite da razão dinâmica linear, quando \(Q \rightarrow P\).

Os exemplos ilustrativos deste método geral foram os seguintes:

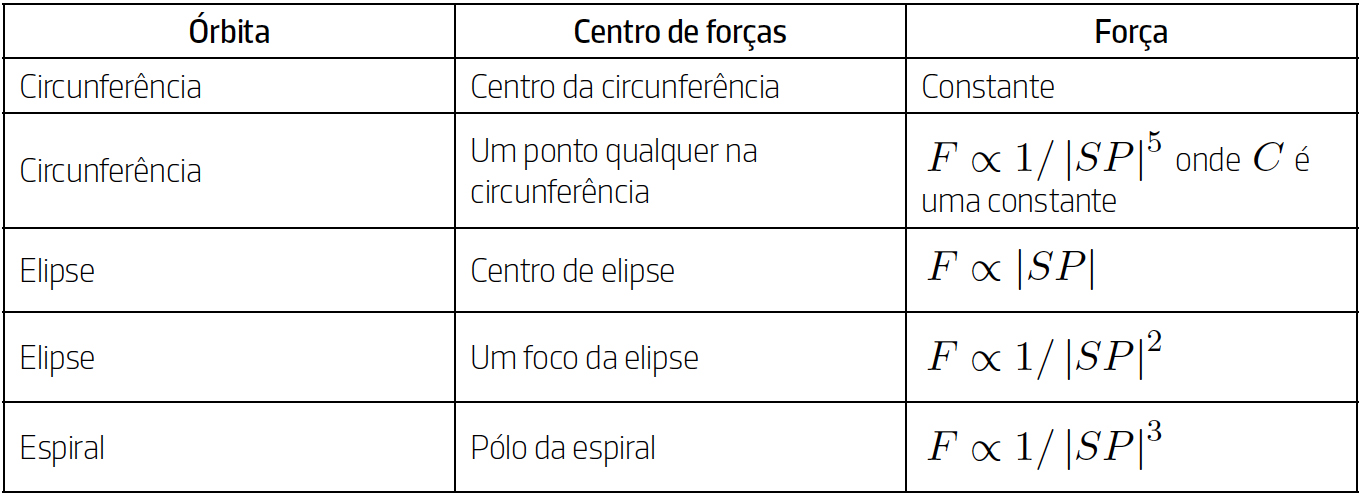
Note que a análise não fez intervir a natureza da órbita de \(P\). Em particular não se supôs que era uma elipse. Newton analisou várias hipóteses para a geometria da órbita. De facto, em 1687 criou um método geral que permite determinar a grandeza da força central responsável por um dado movimento orbital em torno de um centro de forças fixo. Onde o símbolo \(\propto \) significa “proporcional a”.

*

De seguida vamos acompanhar a análise feita por Newton para o caso em que a órbita é uma elipse e \(S\) é um dos focos dessa elipse. Trata-se de um dos argumentos mais famosos em toda a história da ciência e, por isso, vale a pena determo-nos nessa análise.

Newton baseou-se apenas em factos geométricos sobre elipses que conhecia do tratado sobre cónicas de Apolónio de Perga (262-170 a.C.). Vamos começar por listar essas propriedades cuja demonstração se propõe usando métodos de geometria analítica.

5. Algumas propriedades sobre elipses.

A equação geral de uma elipse num sistema de coordenadas cartesiano centrado no seu centro e cujo eixo maior pertence ao eixo dos \(x\)’s, é:

\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

onde \(a\geq b>0\). Os vértices da elipse são os pontos \(\left ( \pm a,0 \right )\) e \(\left ( 0, \pm \right )\) onde ela interseta os eixos coordenados. a diz-se o semi-eixo maior e \(b\) o semi-eixo menor. Um ponto \(P\) da elipse pode ser parametrizado por:

\(P\left ( t \right )=\left ( a\cos t,\sin t \right ),\; \; \; \; \; 0\leq t\leq 2\pi\)

Note que t não é, em geral, o ângulo entre \(\overrightarrow{OP}\) e a parte positiva do eixo dos \(x\)’s.

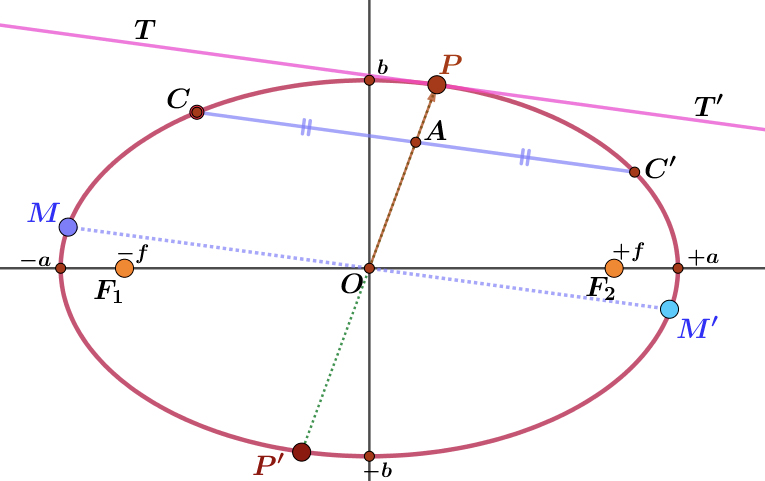
Se definirmos:

\(P'=-P\left ( -a1cos\theta,-b\sin\theta \right )\)

o segmento \(PP′\) passa em \(O\) e diz-se um diâmetro da elipse. Definamos agora dois pontos \(M\) e \(M′\) alterando o parâmetro \(\theta\) de \(\pm\pi /2\):

\(M = (a \cos (\theta + \pi/2) , b \sin (\theta\pi/2))\)

\(= (−a \sin \theta, b \cos \theta)\)

\(M′ = (a \cos (\theta − \pi/2) , b \sin (\theta − \pi/2))\)

\(= (a \sin \theta,−b \cos \theta)\)

O diâmetro \(MM′\) diz-se o diâmetro conjugado ao diâmetro \(PP′\). Note que, em geral, diâmetros conjugados não são perpendiculares entre si.

As propriedades seguintes estão ilustradas na FIGURA 9:

• P1 ... A tangente \(TT′\) à elipse, num ponto \(P\), é paralela ao diâmetro conjugado a \(PP′\).
• P2 ... Qualquer corda da elipse, \(CC′\), paralela à tangente, \(TT′\), à elipse num ponto \(P\), é bissetada pelo diâmetro \(PP′\).
• P3 ... Se a corda \(QQ′\) é paralela à tangente num ponto \(P\) e interseta o diâmetro \(PP′\) num ponto \(V\), então:

\(\frac{\left| PV\right|\times\left| P'V\right|}{\left| QV\right|^{2}}=\frac{\left| OP\right|^{2}}{\left| OM\right|^{2}}\) (5)

onde \(MM′\) continua a ser o diâmetro conjugado a \(PP′\).

• P4 ... A área do paralelogramo cujos lados são as tangentes à elipse nos pontos extremidade de um par de diâmetros conjugados é sempre igual a \(2ab\).

Demonstre analiticamente as 4 propriedades anteriores.

Os focos de uma elipse são os pontos:

\(F_1=\left ( -f,0 \right ),\; \; \; \; \; F_2=\left ( f,0 \right )\)

onde \(f=\sqrt{a^{2}-b^{2}}\).

• P5 ... Se P é um ponto qualquer de uma elipse \(\varepsilon\), então a soma das distâncias de \(P\) aos focos é constante e igual a \(2a\):

\(\left| F_1P\right|+\left| F_2P\right|\equiv 2a,\; \; \; \; \; \forall P\in\varepsilon\)

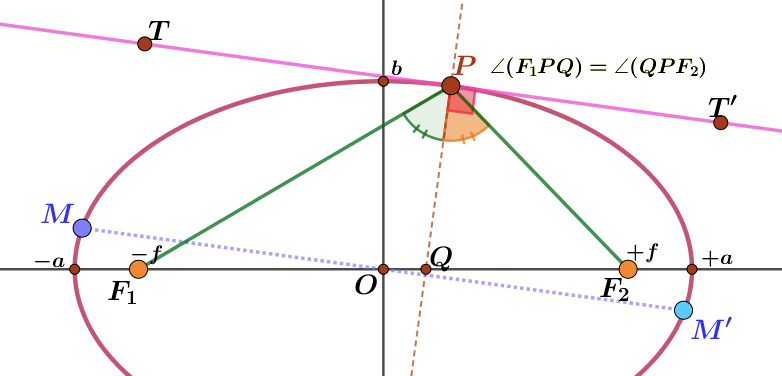
• P6 ... Seja \(P\) um ponto qualquer da elipse. Então a reta que bisseta o ângulo \(\angle(F1PF2)\) é perpendicular à tangente à elipse em \(P\).

Esta é a chamada propriedade refletora da elipse. Num bilhar eliptico, se uma bola, situada num dos focos, é batida em direção ao bordo, então ela passa pelo outro foco (FIGURA 10).

• P7 ... Seja \(P\) um ponto qualquer da elipse, \(MM′\) o diâmetro conjugado a \(PP′\) e \(E\) o ponto de intersecção de \(F_1P\) com \(MM′\) (ver FIGURA 11).

Então a distância \(\left| EP\right|\) é igual ao semi-eixo maior a:

\(\left| EP\right|=a\)

Demonstração (Newton).

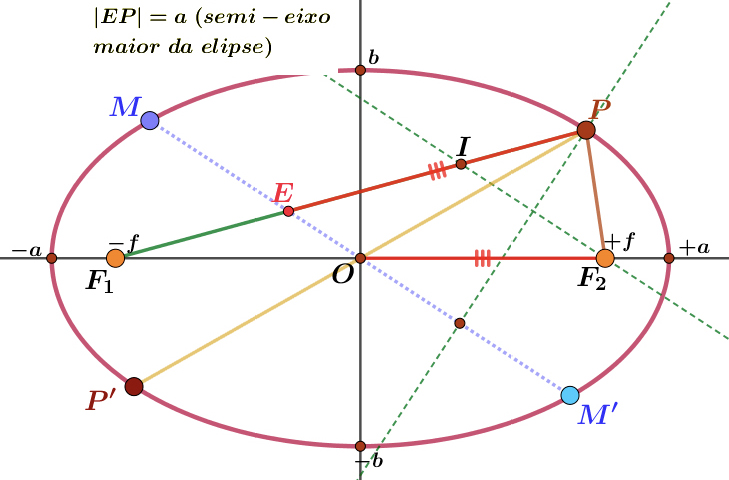
Observe a figura seguinte. \(IF_2\) é paralela a \(MM′\). Desenhamos ainda, a tracejado verde, a bissetriz do ângulo \(\angle(F_1PF_2)\). Pela propriedade 5, essa bissetriz é perpendicular à tangente em \(P\), portanto perpendicular ao diâmetro \(MM′\), pela propriedade 5, e portanto perpendicular ao segmento \(IF^{2}\). Vemos pois que:

\(\left| IP\right|=\left| PF_2\right|\)

Da semelhança dos triângulos \(\Delta (F_1IF_2)\) e \(\Delta (F_1EO)\), e uma vez que \(\left| F_1F_2\right|=2\left| F_1F_2O\right|\), deduzimos que \(\left| F_1I\right|=2\left| F_1E\right|\), isto é:

\(\left| F_1E\right|=\left| EI\right|\)

Pela propriedade 5, vem agora que:

\(2a=\left| F_1P\right|+\left| PF_2\right|\)

\(=\left| F_1E\right|+\left| EP\right|+\left| PF_2\right|\)

\(=\left| EI\right|+\left| EP\right|+\left| IP\right|\) (6)

\(=2\left| EP\right|\Rightarrow \left| EP\right|=a\)

6. Razão dinâmica e cálculo do seu limite, segundo Newton.

Temos agora tudo o que é necessário para analisar como Newton calcula o limite da razão dinâmica:

\(\displaystyle \lim_{Q \to P}\frac{\left| QR\right|}{\left| QT\right|^{2}}\) (7)

quando a trajetória de \(P\) é uma elipse, e portanto calcula a grandeza da força central:

\(F\left ( P \right )=\frac{8\kappa^{2}m}{\left| SP\right|^{2}}\displaystyle \lim_{Q \to P}\frac{\left| QR\right|}{\left| QT\right|^{2}}\) (8)

Vejamos como. Toda a análise refere-se à FIGURA 12, que o próprio Newton usa nos seus Principia:

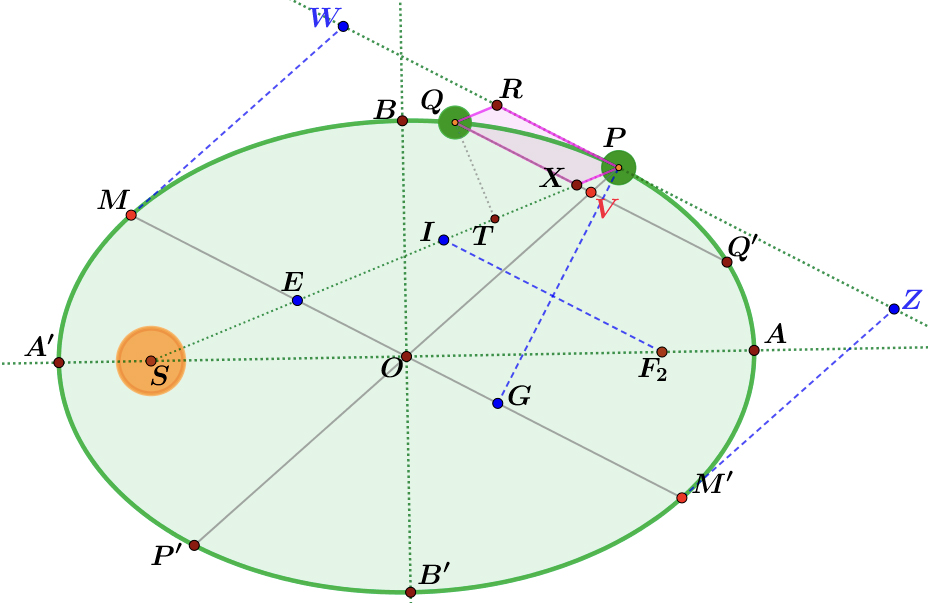
N1. Os triângulos \(\Delta (POE)\) e \(\Delta (PVX)\) são semelhantes. Daí que:

\(\frac{\left| Px\right|}{\left| PV\right|}\frac{\left| PE\right|}{\left| PO\right|}\)

Como \(RQXP\) é um paralelogramo, \(\left| QR\right|=\left| PX\right|\) e como \(\left| PE\right|=a\), pela propriedade 5, substituindo acima vem que:

\(\frac{\left| QR\right|}{\left| PV\right|}=\frac{a}{\left| PO\right|}\) (9)

N2. Apliquemos agora a propriedade 5 à corda \(QQ′\) que interseta o diâmetro \(PP′\) no ponto \(V\). Essa propriedade afirma que:

\(\frac{\left| PV\right|\times\left| P'V\right|}{\left| QV\right|^{2}}=\frac{\left| OP\right|^{2}}{\left| OM\right|^{2}}\)

isto é:

\(\frac{1}{\left| QV\right|^{2}}=\frac{\left| OP\right|^{2}}{\left| OM\right|^{2}}\times\frac{1}{\left| PV\right|\times\left| P'V\right|}\) (10)

N3. Construímos agora \(PG\), perpendicular ao diâmetro \(MM′\) (conjugado a \(PP′\)). É fácil ver que os triângulos retângulos \(\Delta (QTX)\) e \(\Delta (PGE)\) são semelhantes e portanto:

\(\frac{\left| QX\right|}{\left| QT\right|}=\frac{\left| PE\right|}{\left| PG\right|}\)

Como \(\left| PE\right|=a\) vem então que:

\(\frac{\left| QX\right|^{2}}{\left| QT\right|^{2}}=\frac{a^{2}}{\left| PG\right|}\)

Para \(Q\) muito próximo de \(P\), podemos tomar \(\left| QV\right|\approx \left| QX\right|\) nesta fórmula e, resolvendo em ordem a \(1/\left| QT\right|^{2}\) obtemos:

\(\frac{1}{\left| QT\right|^{2}}=\frac{a^{2}}{\left| PG\right|^{2}}\times\frac{1}{\left| QV\right|^{2}}\times\frac{1}{\left| QV\right|^{2}}\) (11)

N4. A área do paralelogramo \(MM′ZW\) (ver figura) é igual a base × altura, isto é, é igual a \(2\left| OM\right|\times\left| PG\right|\) e, pela propriedade 5, essa área é igual a \(2ab\). Portanto, \(2\left| OM\right|\times\left| PG\right|=2ab\) e daí:

\(\frac{a^{2}}{\left| PG\right|^{2}}=\frac{\left| OM\right|^{2}}{b^{2}}\) (12)

N5. O número:

\(l=\frac{2b^{2}}{a}\) (13)

chama-se o lactus rectum principal da elipse.

Insira-se o lactus retum \(l\) e (11) em \(\frac{l\times \left| QR\right|}{\left| QT\right|^{2}}\) e usemos então (12), (10) e (9) para obter sucessivamente o seguinte:

\(\frac{l\times \left| QR\right|}{\left| QT\right|^{2}}=\frac{2b^{2}}{a}\times\left| QR\right|\times\frac{a^{2}}{\left| PG\right|^{2}}\times\frac{1}{\left| QV\right|^{2}}\) por (11)

\(=\frac{2b^{2}}{a}\times\left| QR\right|\times\frac{\left| OM\right|^{2}}{b^{2}}\times\frac{1}{\left| QV\right|^{2}}\) por (12)

\(=\frac{2b^{2}}{a}\times\left| QR\right|\times\frac{\left| OM\right|^{2}}{b^{2}}\times\frac{\left| OP\right|^{2}}{\left| OM\right|^{2}}\times\frac{1}{\left| P'V\right|\times\left| PV\right|}\) por (10)

\(=\frac{2}{a}\times a \times \left| OP\right|^{2}\times\frac{1}{\left| P'V\right|\times\left| PO\right|}\) por (9)

\(=\frac{2\left| OP\right|}{\left| P'V\right|}\)

Portanto:

\(\frac{\left| QR\right|}{\left| QT\right|^{2}}=\frac{2\left| OP\right|}{\left| P'V\right|}\times\frac{1}{l}\)

e quando \(Q\rightarrow P\), \(\left| P'V\right|\rightarrow 2\left| OP\right|\) e daí que:

\(\displaystyle \lim_{Q \to P}\frac{\left| QR\right|}{\left| QT\right|^{2}}=\frac{1}{l}\) (14)

E Newton chega assim ao seu objetivo principal.

N6. Inserindo (14) na fórmula (4) para \(F (P)\) que aqui se recorda:

\(F\left ( P \right )=\frac{8m\kappa^{2}}{\left| SP\right|^{2}}\displaystyle \lim_{Q \to P}\frac{\left| QR\right|}{\left| QT\right|^{2}}\)

obtem-se:

\(F\left ( P \right )=\frac{8m\kappa^{2}}{l^{2}}\times\frac{1}{\left| SP\right|^{2}}\) (15)

Concluindo.

Se um corpo se move sob a ação de uma força central de centro \(S\) e se a sua órbita é uma elipse em que um dos focos é \(S\), então a grandeza dessa força num ponto \(P\) da órbita é igual a:

\(F\left ( P \right )=\frac{8m\kappa^{2}}{l^{2}}\times\frac{1}{r^{2}\left ( P \right )}\) (16)

onde \(r (P)\) é a distância de \(P\) a \(S\), \(\kappa\) é a constante de Kepler da órbita, \(m\) a massa do corpo e \(l=2b^{2}/a\) o lactus retum da elipse.

De facto Newton provou este mesmo resultado também para uma parábola e para uma hipérbole.

Ainda para o caso de uma órbita elítica, seja \(T\) o período da órbita, isto é, o tempo que o corpo demora a percorrer uma volta inteira. Uma vez que a área da elipse é igual a \(\pi ab\) então a constante de Kepler é igual a \(\kappa = \pi ab/T\) e a fórmula de Newton pode escrever-se na forma:

\(F\left ( P \right )=\frac{4m\pi^{2}a^{3}}{T^{2}}\times\frac{1}{r^{2}\left ( P \right )}\) (17)

\(F (P)\) é pois o valor da força gravitacional com a qual um corpo \(S\) atrai um corpo \(P\) de massa m situada a uma distância \(r (P)\) de \(S\). Newton aplica a sua teoria ao movimento dos planetas em volta do Sol.

Reescrevendo o valor da força na forma:

\(F_P=C_Pm\frac{1}{r^{2}}\)

onde \(C_P = 8\kappa^2/l\). Se \(S\) exerce uma força de atração sobre \(P\), \(P\) também exerce uma força de atração sobre \(S\). De facto, pela 3.ª lei de Newton, a força \(F (P)\) com que \(S\) atrai \(P\) tem uma reação igual mas oposta. Por outras palavras, \(P\) atrai \(S\) com uma força de grandeza \(F_S = F_P\) na direção oposta à que \(S\) atrai \(P\).

A simetria da situação exige que:

\(F_S=C_SM\frac{1}{r^{2}}\)

onde \(M\) é a massa de \(S\) e \(C_S\) é uma constante. Como \(F_S = F_P\) vemos que \(C_SM = C_Pm\) e portanto:

\(\frac{C_P}{M}=\frac{C_S}{m}\doteq G\)

Notando que \(GM = C_P\) e \(Gm = C_S\) e pondo \(F = F_P = F_S\) obtemos:

\(F=G\frac{mM}{r^{2}}\) (18)

que é a famosa lei da atração universal de Newton. \(G\) é uma constante universal independente dos corpos em questão.