Considere-se o eixo \(x\) marcado por pontos igualmente espaçados e identificados por um número inteiro , tomando-se \(n=0\) para origem. Imagine-se que, partindo da origem, uma partícula, a cada tique \(\tau\) de um relógio \(\left ( \tau=0,1,2,\cdots \right )\) efetua um salto aleatório para o ponto à direita com probabilidade \(p\), ou para a esquerda com probabilidade \(q=1-p\). Então, a probabilidade \(P_n\left ( \tau \right )\) de a partícula se localizar no ponto \(n\) no “instante” \(\tau\) satisfaz a equação:

\(P_n\left ( \tau+1 \right )=pP_{n-1}\left ( \tau \right )+qP_{n+1}\left ( \tau \right )\) (1)

com a condição inicial:

\(P_n\left ( 0 \right )=\delta_{n,0}\) (2)

onde \(\delta_{i,j}\) é o símbolo de Kronecker. A equação 1 é um caso particular da, assim designada, equação-mestra:

\(P_n\left ( \tau+1 \right )=\sum_{m}^{}W_{n,m}P_m\left ( \tau \right )\) (3)

onde \(W_{n,m}\geq 0\) é a probabilidade de transição de \(m\) para satisfazendo à condição de conservação de probabilidade:

\(\sum_{n}^{}W_{n,m}=1\) (4)

Muitos problemas interessantes podem ser formulados usando a equação 3, desde propagação de vírus ou fogos florestais até oscilações da bolsa de valores (consideradas numa nova área conhecida por Econofísica).

É fácil verificar que a equação 1 é reproduzida pela equação 3 com a escolha \(W_{n,m}=p\delta_{n,m+1}+q\delta_{n,m-1}\). O cálculo da média e outros momentos da distribuição \(P_n\left ( \tau \right )\) pode ser feito a partir da equação 3; por exemplo:

\(\langle n(\tau) \rangle = \sum_n n P_n(\tau) \rightarrow \langle n(\tau + 1) \rangle = \langle n(\tau) \rangle + p - q\) (5)

\(\langle n^2(\tau) \rangle = \sum_n n^2 P_n(\tau) \rightarrow \langle n^2(\tau + 1) \rangle = \langle n^2(\tau) \rangle + 2(p - q)\langle n(\tau) \rangle + 1\)

Tendo em atenção a condição inicial, obtém-se a média e a variância da distribuição:

\(\langle n(\tau)\rangle=(p-q)\tau\) (7)

\(\sigma^{2}(\tau)\equiv\left\langle n^{2}(\tau)\right\rangle-\left\langle n(\tau)\right\rangle^{2}=4pq\tau\) (8)

Estes resultados sugerem que, para \(\tau\gg 1\), a distribuição \(P_n\left ( \tau \right )\) se aproxima de uma Gaussiana centrada na média e com uma largura \(\sigma \left ( \tau \right )\), isto é, a partícula situa-se em \(\langle n\left ( \tau \right )\rangle\) com um “erro” \(3\times \sigma\left ( \tau \right )\).

A própria distribuição \(P_n\left ( \tau \right )\) pode ser obtida usando o método da função geradora. Defina-se:

\(\phi(k,\tau)=\sum_nP_n(\tau)e^{ikn}\) (9)

Notar-se-á que \(k\) e \(k+2\pi\times\) inteiro dão o mesmo resultado, pelo que se restringe \(k\) ao intervalo \(\left ] -\pi,\pi \right ]\). Também se registam as seguintes propriedades:

conservação de probabilidade \(\to \phi\left ( 0,\tau \right )=1\)

condição inicial \(\to \phi\left ( k,0 \right )=1\)

Ora, usando a equação 1, obtém-se:

\(\phi(k,\tau+1)= \begin{pmatrix} pe^{ik}+qe^{-ik} \end{pmatrix}\phi(k,\tau)\to\phi(k,\tau)= \begin{pmatrix} pe^{ik}+qe^{-ik} \end{pmatrix}^\tau\) (10)

Desenvolvendo esta potência e comparando com a equação 9, tem-se:

\(P_n(\tau)=\sum_{l=0}^{\tau}\binom{\tau}{l}p^lq^{\tau-l}\delta_{n+\tau,2l}\) (11)

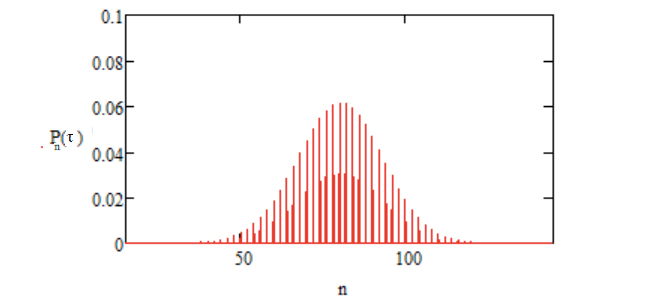
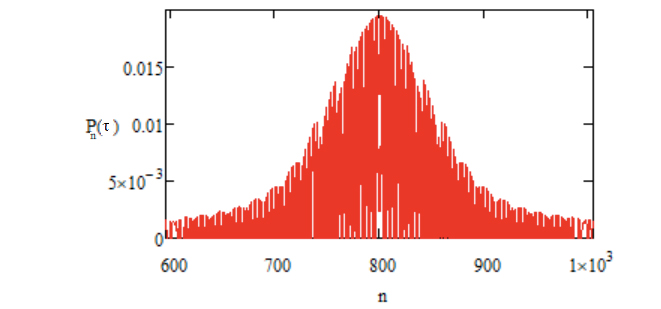
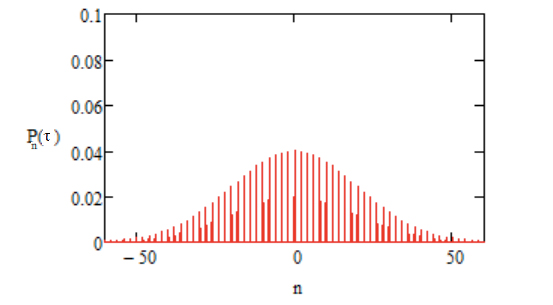
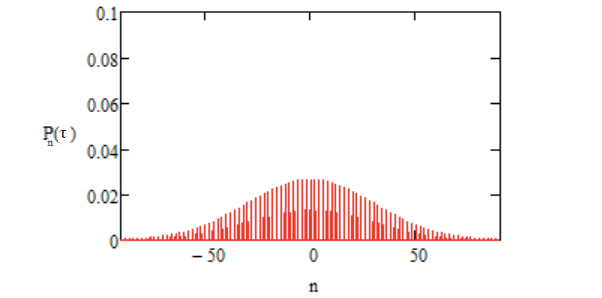
Esta distribuição está representada nas FIGURAS 2 e 3, para \(p=0,7\). Elas mostram claramente que se aproxima de uma Gaussiana para \(\tau\gg 1\).

Um método alternativo para se obter \(P_n\left ( \tau \right )\) a partir de \(\phi\left ( k,\tau \right )\) consiste em começar por verificar a identidade:

\(\frac{1}{2\pi}\int_{-\pi}^{\pi}dke^{ik(m-n)}=\delta_{m,n}\quad m,n\) inteiros (12)

Deste modo, a equação 9 pode ser invertida, obtendo-se:

\(P_n(\tau)=\frac{1}{2\pi}\int_{-pi}^{\pi}dke^{-ikn}\phi(k,\tau)\) (13)

reproduzindo-se a equação 11.

Com a função geradora é fácil calcular momentos da distribuição \(P_n\left ( \tau \right )\). Por exemplo:

\(\left(\frac{\partial\phi}{\partial k}\right)_{k=0}=i\langle n(\tau)\rangle\) (14)

\(\left(\frac{\partial^2\phi}{\partial k^2}\right)_{k=0}=-\langle n^2(\tau)\rangle\) (15)

Usando a equação 10, confirmam-se facilmente os resultados (7) e (8).

O caso \(p=q=\frac{1}{2}\), porque foi considerado por Einstein na sua segunda publicação sobre o movimento Browniano (1905) e pela sua relação com a difusão macroscópica, merece uma atenção particular.

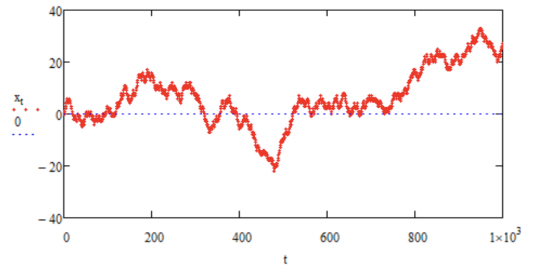
A FIGURA 4 mostra o resultado da simulação das posições visitadas pela partícula para um total de 103 saltos. A partir destes resultados foi obtido o histograma da FIGURA 5 onde, para cada posição (eixo horizontal), é indicado o número de visitas (eixo vertical). Detalhes são remetidos para o Apêndice.

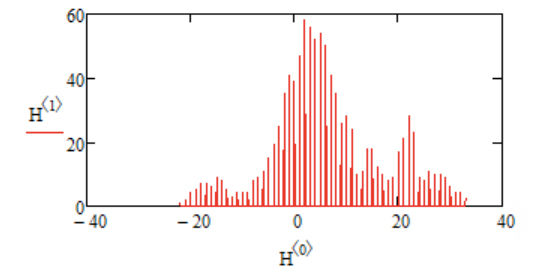
O histograma já é uma boa aproximação para a distribuição exacta dada pela equação 11. Esta distribuição está representada nas FIGURAS 6 e 7 para \(\tau=400\) e \(\tau=900\), respetivamente, verificando-se o aumento da sua largura conforme a equação 8, por exemplo,

\(\sigma\left ( \tau \right )=\sqrt{\tau}\) (16)

Se a distância entre saltos consecutivos for \(a\) e o intervalo de tempo entre dois cliques consecutivos for \(\Delta t\), então o desvio padrão nas posições da partícula escreve-se:

\( \sigma\left ( t \right )=a\sqrt{\frac{t}{\Delta t}}=\sqrt{2Dt}\) (17)

onde se identifica:

\(D=\frac{a^2}{2\Delta t}\) (18)

Adiante será mostrado que \(D\) é o coeficiente de difusão para um conjunto de partículas imersas num fluido. A equação 17, devida a A. Einstein (1905) foi verificada por J. Perrin em 1908 através da observação ao microscópio do movimento aleatório de partículas suspensa num fluido. Por este trabalho, Perrin receberia o Prémio Nobel da Física de 1926.

Tendo a partícula partido da origem, tem interesse saber se à origem ela pode voltar, pela primeira vez, ao fim de um número arbitrário de saltos. É claro que, por exemplo, para dois saltos apenas, a partícula pode regressar à origem com probabilidade \(\frac{1}{2}\), correspondente às transições \(0\to 1\to 0\) e \(0\to -1\to 0\). Contudo, a partícula pode afastar-se muito da origem e, eventualmente, nunca a ela regressar. Para responder à questão, verifica-se que a solução formal da equação 3 é:

\(P_n(\tau)=\left[W^t\right]_{n,0}\) (19)

onde \(W\) a matriz já foi definida, por exemplo, \(W_{n,m}=\frac{1}{2}(\delta_{n,m+1}+\delta_{n,m-1})\). Então, formalmente, tem-se:

\(P_{0}(\tau)=\left[W^{\tau}\right]_{0,0}=\sum_{n_{1}}\sum_{n_{2}}\cdots\sum_{n_{\tau}}W_{0,n_{1},n_{2}}\cdots W_{n_{\tau},0}\)

Há, assim, termos onde um ou mais dos índices podem tomar o valor 0, representando, pois, um retorno à origem. Designe-se por \(R\left ( \tau \right )\) a contribuição para \(P_0\left ( \tau \right )\) dos termos em que nenhum índice tem o valor 0, por exemplo, \(R\left ( \tau \right )\) é a probabilidade de a partícula regressar, pela primeira vez, à origem ao fim de \(\tau\) saltos. Mas também há termos em que, apenas um índice qualquer, por exemplo \(n_{\tau_{1}}\) é nulo, o que significa que a partícula regressa à origem ao fim de \(\tau_1\) saltos e volta a regressar ao fim \(\tau-\tau_1\) de saltos; a soma destes termos é \(\sum_{\tau_{1}}R(\tau_{1})R(\tau-\tau_{1})\).

Percebe-se como este processo se itera, obtendo-se:

\(P_{0}(\tau)=R(\tau)+\sum_{\tau_{1}}R(\tau_{1})R(\tau-\tau_{1})+\sum_{\tau_{1}}\sum_{\tau_{2}}R(\tau_{1})R(\tau_{2})R(\tau-\tau_{1}-\tau_{2})+\cdots\) (20)

Definindo:

\(\tilde{P}_0(s)=\sum_{\tau=0}^\infty e^{-s\tau}P_0(\tau)\)

E, analogamente,

\(\tilde{R}(s)=\sum_{\tau=0}^\infty e^{-s\tau}R(\tau)\)

Conclui-se:

\(\tilde{P}_{0}(s)=\frac{\tilde{R}(s)}{1-\tilde{R}(s)}\to\tilde{R}(s)=\frac{1}{1+\tilde{P}_{0}^{-1}(s)}\)

O cálculo de \(\tilde{P}_0\left ( s \right )\) pode ser feito a partir das eqs. (13) e (10):

\(\tilde{P}_{0}(s)=\sum_{\tau=0}^{\infty}e^{-s\tau}\frac{1}{2\pi}\int_{-\pi}^{\pi}dk(\cos k)^{\tau}=\frac{1}{2\pi}\int_{-\pi}^{\pi}dk\frac{1}{1-e^{-s}\cos k}\)

Ora, a probabilidade de a partícula regressar à origem pela primeira vez seja qual for o número de passos é, simplesmente, \(\tilde{R}(0)=\frac{1}{1+\tilde{P}_{0}^{-1}(0)}\). Mas \(\tilde{P}_{0}(0)=\frac{1}{2\pi}\int_{-\pi}^{\pi}dk\frac{1}{1-\cos k}=\infty\), pelo que \(\tilde{R}\left ( 0 \right )=1\) - a partícula regressa certamente à origem. É interessante sublinhar que este resultado é exacto para o movimento aleatório a uma dimensão, sendo marginal para duas dimensões (\(\tilde{P}_0\left ( 0 \right )\) diverge logaritmicamente) e \(\tilde{R}_0\left ( 0 \right )=0,603\) para três dimensões.

Passagem ao contínuo – difusão e equação de Fick.

Imagine-se que há \(N\) partículas independentes, cada uma executando um movimento aleatório descrito pela equação 1. É mais natural estudar tal sistema através de uma descrição macroscópica caracterizada por uma densidade \(n\left ( x,t \right )=NP\left ( x,t \right )\) onde \(P\left ( x,t \right )\) é a versão de \(P_n\left ( \tau \right )\) para tempo e espaço contínuos. Para isso, aceita-se que a distância entre pontos vizinhos atrás considerada, é um pequeno comprimento e que o tempo real \(\Delta t\) entre dois tiques do relógio é, também pequeno. Em ambos os casos, por pequeno entende-se que a densidade, e outras grandezas macroscópicas, pouco variam naqueles intervalos de espaço e tempo. Nestas condições, define-se:

\(P\left ( x,t \right )a=P_n\left ( \tau \right )\) (21)

Com a correspondência:

\(x=na\)

\(t=\tau\Delta t\)

pelo que:

\(P\left ( x\pm a,t \right )a=P_{n\pm 1}\left ( \tau \right )\)

\(P\left ( x,t+\Delta t \right )a=P_{n}\left ( \tau+1 \right )\)

Assim, a equação 1 fica:

\(P(x,t+\Delta t)a=[pP(x-a,t)+qP(x+a,t)]a\)

o que, depois de cancelar o factor a comum e de multiplicar por \(N\), se converte em:

\(n(x,t+\Delta t)=pn(x-a,t)+qn(x+a,t)\)

Desenvolvendo até à 1.ª ordem no tempo e 2.ª ordem em \(x\), obtém-se:

\(\frac{\partial n}{\partial t}=-v\frac{\partial n}{\partial x}+D\frac{\partial^{2}n}{\partial x^{2}}\) (22)

onde:

\(v=(p-q)\frac{a}{\Delta t}\) (23)

é a velocidade macroscópica da partícula; e:

\(D=\frac{a^2}{2\Delta t}\) (24)

como atrás se encontrou. As eqs. (23) e (24) exibem o relacionamento de grandezas mensuráveis da partícula com grandezas definidas para o movimento Browniano.

A versão no contínuo da condição inicial definida pela equação 2 fica:

\(n(x,0)=\frac{\delta_{n,0}}{a}=\frac{1}{2\pi}\int_{-\pi}^\pi\frac{dk}{a}e^{ikn}=\frac{1}{2\pi}\int_{-\frac{\pi}{a}}^{\frac{\pi}{a}}dqe^{iqx}\xrightarrow{}\delta(x)\) (25)

onde se usou a equação 12. O resultado final é a distribuição \(\delta\) de Dirac.

A equação 22 tem a forma de uma lei de conservação (cf. a lei de conservação de carga em Electromagnetismo). Trata-se, de facto da conservação do número total de partículas. Rescrevendo aquela equação:

\(\frac{\partial n}{\partial t}=-\frac{\partial J}{\partial x}\) (26)

com:

\(J(x,t)=vn(x,t)-D\frac{\partial n}{\partial x}\) (27)

Identifica-se \(J\left ( x,t \right )\) como o fluxo do número de partículas, aparecendo como a sobreposição de um movimento macroscópico associado com a velocidade, com um movimento dispersivo, como a seguir se mostra. Com efeito, a solução da equação 22, sujeita à condição inicial expressa pela equação 25 pode ser obtida por simples transformação de Fourier. Escrevendo:

\(n(x,t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}dke^{ikx}\psi(k,t)\) (28)

obtém-se:

\(\frac{\partial\psi}{\partial t}=-\left(ikv+Dk^{2}\right)\psi\)

com a condição inicial \(\psi\left ( k,0 \right )=1\), pelo que \(\psi(k,t)=e^{-\left(ikv+Dk^{2}\right)t}\). Substituindo na equação 28 e integrando, tem-se:

\(n(x,t)=\frac{1}{\sqrt{4\pi Dt}}e^{-\frac{(x-vt)^2}{4Dt}}\) (29)

Esta distribuição Gaussiana desloca-se com a velocidade v aumentando a sua largura como \(\sqrt{2Dt}\). Quando se deita um pingo de tinta colorida solúvel em água, vê-se que a tinta se desloca para baixo pela acção da gravidade e se vai alargando por acção da difusão até se atingir um equilíbrio, com mais tinta em baixo e menos em cima. Ambos os fenómenos resultam do movimento Browniano de cada partícula da tinta.

A expressão do fluxo com \(v=0\), por exemplo, \(J=-D\frac{\partial n}{\partial x}\) foi postulada em 1855 por Adolf Fick nos seus estudos sobre difusão, sendo \(D\) conhecida por constante de difusão, ficando aquela expressão a ser conhecida por lei de Fick. A lei traduz um fenómeno bem conhecido: partículas tendem a deslocar-se da região de maior concentração para a região de menor concentração. A relação da constante de difusão com características do movimento Browniano, equação 24, foi estabelecida por A. Einstein no seu primeiro artigo de 1905 sobre aquele movimento.

Mas há, também, um outro caso de muito interesse: quando a tinta colorida atrás referida atinge uma situação de equilíbrio, o fluxo anula-se. Ora, nesta situação, a distribuição das partículas segue a lei de Maxwell-Boltzmann: considerando o eixo vertical, dirigido para cima, a distribuição de equilíbrio é \(n(x)\propto e^{-\beta mgx}\), onde \(\beta^{-1}=k_{b}T\) (\(k_B\) constante de Boltzmann; \(T\) temperatura absoluta do fluido onde se processa a difusão). Deste modo, a condição \(J=0\) na equação 27 dá:

\(v+\beta mgD=0\) (30)

Mas observe-se agora que cada partícula, embora muito pequena, é muito maior que as moléculas do fluido, estando, segundo as leis da Mecânica, sujeita quer à força da gravidade, quer à força exercida pela viscosidade do fluido que se opõe ao movimento. Assuma-se que esta força é dada pela fórmula de Stokes para partículas esféricas (raio ), por exemplo, \(6\pi\eta rv\). Quando as duas forças se equilibram, atingindo-se uma velocidade constante (velocidade terminal) então:

\(mg+6\pi\eta rv=0\) (31)

Comparando estas duas expressões, obtém-se:

\(D=\frac{k_BT}{6\pi\eta r}\) (32)

A importância histórica desta equação, por A. Einstein no seu primeiro artigo de 1905 sobre o movimento Browniano deve ser realçada: como \(k_{B}=\frac{R}{N_{A}}\), onde \(R\) é a constante dos gases perfeitos, a equação 32 permite determinar \(N_A\) o número de Avogadro, uma enorme contribuição para a aceitação da realidade de átomos.

Modernamente, considera-se a equação 32 como um exemplo do teorema da flutuação dissipação: a dissipação, um fenómeno irreversível macroscópico, assenta nas flutuações microscópicas que inevitavelmente o meio apresenta.

O impacto dos trabalhos de Einstein sobre o movimento Browniano e difusão pode avaliar-se pelas posições assumidas pelo famoso químico W. Ostwald: antes da publicação daqueles trabalhos, Ostwald não acreditava na hipótese atómica; após aquelas publicações e as experiências de Perrin, ficou convencido da existência de átomos, tendo proposto Einstein para o Nobel da Física em 1910!

Entropia e irreversibilidade num modelo simples.

Regressando à equação 3, admita-se agora que \(n\) identifica estados quânticos de um sistema isolado, por exemplo, soluções da equação de Schroedinger para a mesma energia. Pequenas interacções ignoradas naquela equação originam transições entre os estados. Num modelo simples, admitir-se-á que, de um qualquer estado, se pode saltar para qualquer outro com igual probabilidade. Sendo \(N\) o número total de estados do sistema, então:

\(W_{n,m}=\frac{1}{N-1}(1-\delta_{nm})\) (33)

Inserindo na equação-mestra (equação 3), obtém-se:

\(P_n(\tau+1)=\frac{1}{N-1}(1-P_n(\tau))\) (34)

É imediato verificar que existe uma solução estacionária definindo um estado de equilíbrio:

\(\bar{P_n}=\frac{1}{N}\) (35)

Esta solução é um atractor para qualquer distribuição inicial. Com efeito, fazendo:

\(P_n(\tau)=\bar{P}_n+P_n^{^{\prime}}(\tau)\)

deduz-se:

\(P_{n}^{^{\prime}}(\tau+1)=-\frac{1}{N-1}P_{n}^{^{\prime}}\to P_{n}^{^{\prime}}(\tau)=\left(-\frac{1}{N-1}\right)^{t}P_{n}^{^{\prime}}(0)\to0\)

Na definição de Boltzmann, a entropia do sistema no estado de equilíbrio é:

\(S_e=ln(N)\)

Na definição de W. Gibbs, a expressão da entropia é definida mesmo fora de equilíbrio:

\(S(\tau)=-\sum_{n=1}^NP_n(\tau)ln(P_n(\tau))\) (36)

Como \(P_{n}(\tau)\to\bar{P}_{n}\), então \(S(\tau)\to-\sum_{n=0}^{N}\left(\frac{1}{N}\right)ln\left(\frac{1}{N}\right)=lnN=S_{e}\).

Vai agora mostrar-se que, seja qual for \(P_n\left ( \tau \right )\) na equação 36, é sempre \(S\left ( \tau \right )\leq S_e\). Tal significa que se o estado inicial do sistema for de não equilíbrio, a entropia de Gibbs evolui para o seu máximo que é a entropia de Boltzmann. Como a variável \(\tau\) não participa na demonstração, ela será omitida.

Seja \(P_n\) uma distribuição arbitrária e defina-se o seu expoente de probabilidade, \(\omega_n\) por:

\(P_n\equiv e^{-\omega_n}\)

Para a distribuição uniforme, \(\bar{P_n}\), o seu expoente é simplesmente \(\bar{\omega_{n}}=ln(N)\), independente do índice \(n\). A condição de normalização à unidade escreve-se:

\(\sum_{n=1}^Ne^{-\omega_n}=\sum_{n=1}^Ne^{\bar{\omega_n}}=1\)

Daqui resulta a identidade:

\(\frac{1}{N}\sum_{n=1}^{N}\left(e^{-(\omega_{n}-\bar{\omega}_{n})}-1\right)=0\) (37)

Considere-se a entropia de Gibbs:

\(S=-\sum_{n=1}^NP_nlnP_n=\sum_{n=1}^n\omega_ne^{-\omega_n}\)

Para o equilíbrio:

\(S_e==\sum_{n=1}^n\bar{\omega}_ne^{-\bar{\omega}_n}=ln(N)\)

Ora:

\(S_e-S=\sum_{n=1}^N\left(\bar{\omega}_ne^{-\bar{\omega}_n}-\omega_ne^{-\omega_n}\right)=\frac{1}{N}\sum_{n=1}^N(\bar{\omega}_n-\omega_n)e^{-(\omega_n-\bar{\omega}_n)}\)

A última expressão resulta da uniformidade de \(\bar{\omega}_{n}=ln(N)\) e da condição de normalização. Ora, para qualquer \(x\) real é \(x\geq1-e^{-x}\) como consequência da concavidade da exponencial. Considerando \(x=\bar{\omega}_{n}-\omega_{n}\) na expressão anterior, obtém-se:

\(S_e-S\geq\frac{1}{N}\sum_{n=1}^{N}\left(1-e^{-(\overline{\omega}_n-\omega_n)}\right)e^{-(\omega_n-\overline{\omega}_n)}=\frac{1}{N}\sum_{n=1}^{N}\left(e^{-(\omega_n-\overline{\omega}_n)}-1\right)=0\)

como resulta da equação 37.

Este modelo, embora bastante simplista, contém os conceitos e métodos essenciais da Física Estatística a qual, por si só, será considerada em artigos futuros.

Apêndice: Simulação do movimento aleatório.

A simulação de um processo estocástico, tal como genericamente formulado na equação 3, é uma experiência realizada em computador onde aquele processo é implementado. Pode ser efetuado com uma linguagem de programação, um programa científico de Matemática ou uma simples folha de cálculo como aqui será considerado. Para simular a equação 1, selecionamse duas colunas, e.g., A e B, colocando-se a letra t em A1 (título para os saltos) e a letra n em B1 (título para a posição). Em A2 e B2 entra-se 0 e 0 para a condição inicial. Aceitando que a simulação é para 100 passos (embora preferível um número muito maior, mas na prática limitado pela capacidade da folha de cálculo), preenche-se A3 até A102 com 1, 2,…,100. Em B3 introduz- se a fórmula B2+SE(ALEATÒRIO \(\leq \) p,1,-1). A função ALEATÓRIO gera um número aleatório uniformemente distribuído em [0,1]; a função SE compara esse número com a probabilidade p (salto para a direita), selecionando 1 se o número for inferior ou igual a p, ou -1 no caso de o número ser superior a p. O número selecionado é adicionado a B2. A fórmula é copiada e colada em B4 até B102, ficando assim geradas as sucessivas posições da partícula. Podem ser representados num gráfico de pontos seleccionando A2:B102. A média e variância das posições são obtidas com as funções MÉDIA e VARIÂNCIA sendo, respetivamente, colocadas em C1 e D1. A frequência com que um dado ponto n é visitado pode ser obtido com a função HISTOGRAMA (se existir na folha de cálculo) ou por simples contagem como agora se refere. Na célula E50 entra-se 0 e preenche-se E39 a E60 com -10, -9,...,9,10 por ordem crescente. Em F50 entra-se a função CONTAR:SE($B$2:$B$102;E50) que conta quantas vezes aparece 0 nos dados da coluna B. Copiando a fórmula para as células F39 a F60, obtém-se contagem similar para os outros inteiros em [-10,10]. Um gráfico (de barras) destes resultados é uma aproximação a \(P_n\left ( \tau \right )\), tanto melhor quanto maior for o número de saltos. As FIGURA 8 e FIGURA 9 mostram os resultados de uma tal simulação.

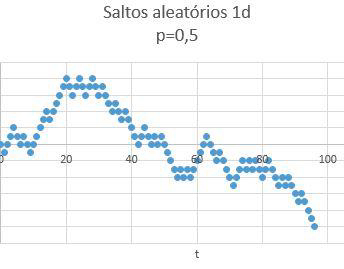
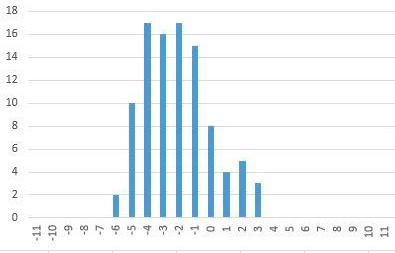
Uma folha de cálculo tem dois pontos fracos: a limitação no número de saltos e o gerador de números aleatórios. Programas científicos de Matemática apresentam melhores geradores e permitem fazer simulações para muito maior número de saltos, para além de fornecerem funções que automatizam a geração de histogramas. As FIGURAS 4 e 5 foram obtidas num desses programas para p=1/2.