Da segunda lei de Newton,

\(\overrightarrow{F}=m\overrightarrow{a}\)

decorre facilmente o chamado teorema da energia cinética. Tomando o produto escalar de ambos os membros pela velocidade do corpo, \(\overrightarrow{v}\).

\( \overrightarrow{F}\cdot \overrightarrow{v}=m\overrightarrow{a}\cdot\overrightarrow{v}\) (1)

Daqui podíamos facilmente obter o teorema de energia cinética na forma mais geral, usando derivação e integração; esses conceitos não são necessários no caso de força constante. A dedução é menos elegante mas mais acessível.

Nesse caso, o movimento é uniformemente acelerado e

\(\Delta \overrightarrow{v}=\overrightarrow{v}\left ( t+\Delta t \right )-\overrightarrow{v}\left ( t \right )=\overrightarrow{a}\Delta t\) (2)

\(\Delta\overrightarrow{r}=\overrightarrow{v}\left ( t \right )\Delta t+\frac{1}{2}\overrightarrow{a}\Delta t^2\) (3)

O trabalho realizado no deslocamento \(\Delta \overrightarrow{r}\)

\(\overrightarrow{F}\cdot\Delta\overrightarrow{r}=\overrightarrow{F}\cdot\overrightarrow{v}\Delta t+\frac{1}{2}\overrightarrow{F}\cdot\overrightarrow{a}\Delta t^2\) (4)

Usando a segunda Lei de Newton:

\(\overrightarrow{F}\cdot \Delta\overrightarrow{r}=m\overrightarrow{a}\cdot\overrightarrow{v}\Delta t+\frac{1}{2}ma^2\Delta t^2=m\Delta \overrightarrow{v}\cdot\overrightarrow{v}+\frac{1}{2}m\Delta v^2\) (5)

O segundo membro é a variação de energia cinética

\(m\Delta\overrightarrow{v}\cdot\overrightarrow{v}+\frac{1}{2}m\Delta v^2=\frac{m}{2}\left [ \left ( \overrightarrow{v}+\Delta\overrightarrow{v} \right )^{2}-\overrightarrow{v}^{2} \right ]\) (6)

Que há de errado neste dedução? Nada. Este resultado,

\(\overrightarrow{F}\cdot \Delta\overrightarrow{r}=\Delta\left ( \frac{1}{2}mv^{2} \right )\) (7)

é de aplicação tão universal como a segunda lei de Newton, apesar de só o termos demonstrado no caso de força constante^a. É então sempre verdade que o trabalho das forças externas é a variação de energia cinética?

Não! De seguida vamos analisar dois exemplos que clarificam esta questão. No primeiro caso, o trabalho das forças externas é negativo e a energia cinética aumenta e, no segundo caso, o trabalho das forças externas é o dobro da variação da energia cinética.

Saltar.

Consta que todos os mamíferos, à exceção do elefante, aprendem a saltar. Para bípedes, como os humanos, a ação consiste em começar por fletir as duas pernas, depois empurrar o chão, esticando- as; os pés perdem contacto com o solo na extensão máxima das pernas e pés. Que força externa é responsável pelo movimento ascendente do centro de massa da pessoa que salta?

Obviamente, a força exercida pelo solo nos seus pés durante a extensão. Se o centro de massa subir uma distância \(h\), entre o início do movimento das pernas e o momento em que os pés perdem contacto com o solo, temos, se admitirmos que a força externa \(F_e\) é constante,

\(\overrightarrow{F}\cdot \Delta\overrightarrow{r}=\left ( F_e-mg \right )h\) (8)

Pelo teorema da energia cinética,

\(\Delta E_c=\frac{1}{2}m\left ( v_{cm}^{2}-0 \right )=\left ( F_e-mg \right )h\) (9)

ou seja,

\(v_{cm}^{2}=2\left ( \frac{F_e-mg}{m} \right )h\) (10)

Certo? Sem dúvida, limitamo-nos a aplicar o teorema de energia cinética a este exemplo.

Mas pensemos um pouco. A força do solo está aplicada na planta dos pés. Enquanto estes estão em contacto como o solo, o seu deslocamento é nulo; quando perdem contacto com o solo, a força \(F_e\) anula-se. A conclusão só pode ser uma: o trabalho da força do solo é nulo! O único trabalho externo é o do peso e este é negativo. Mas a variação de energia cinética é positiva. Por isso o trabalho das forças externas não é a variação de energia cinética.

Aqui reside o equívoco. O primeiro membro do teorema da energia cinética não é o trabalho das forças externas. É simplesmente o valor do produto da resultante das forças externas pelo deslocamento do centro de massa. Parece um trabalho, mas nem sempre é. No caso do salto não é!

Aliás seria estranho se fosse. A realização de trabalho assinala uma transferência de energia. Ora, não é do solo que vem a energia que surge como energia de translação do centro de massa. Era bom! Se assim fosse, poderíamos estar meia-hora aos pulos sem nos cansarmos. De onde vem então essa energia?

Da energia interna do corpo que salta. A interação com o solo permite a transferência de energia interna para energia de translação do centro de massa (pela lei da inércia esta transformação seria impossível para um corpo isolado), mas o que o solo transfere não é energia – não realiza trabalho – mas sim momento linear: a força é a taxa de transferência de momento, do solo para o corpo que salta. Contudo, reafirmo, não há nada de errado com o resultado deduzido para a velocidade do centro de massa. Mas é errado pensar a respetiva dedução em termos de balanço de energia!

Em abono da verdade, a maior parte dos manuais apresenta o teorema de energia cinética no contexto da mecânica de uma partícula material, caso em que \(\overrightarrow{F}\cdot\Delta \overrightarrow{r}\) é efetivamente o trabalho das forças externas¹. Mas ao mesmo tempo, os exercícios e problemas propostos referem- se quase sempre a corpos extensos. O teorema mantém exatamente a mesma forma, mas é importante lembrar que, nesse caso, \(\overrightarrow{F}\cdot\Delta r\) pode não ser o trabalho das forças externas sobre o corpo.

Arrastado pelo elétrico.

O segundo exemplo é mais curioso e muito menos discutido.

Quem conhece os elétricos que ainda circulam no Porto e em Lisboa, sabe que não têm portas (ou as têm abertas) e que a entrada se faz por um degrau com um corrimão vertical. Na minha adolescência era, sem dúvida, o meio de transporte mais usado na cidade do Porto. Muitas vezes, já com o elétrico em movimento, agarrávamos o corrimão e éramos arrastados para o degrau. Ninguém dentro do elétrico sentia qualquer variação de velocidade do mesmo como consequência deste evento: a variação de velocidade do elétrico era desprezável.

É precisamente esta situação que pretendo examinar. Um corpo, inicialmente em repouso, é atuado por uma força cujo ponto de aplicação se desloca a velocidade constante, como no caso do elétrico, ou de um(a) ciclista que se atrela a um camião TIR em movimento. Eventualmente o corpo acaba por ter a mesma velocidade que o ponto de aplicação da força. Neste caso, como veremos, o trabalho da força externa é o dobro da variação de energia cinética de translação.

Este resultado prova-se com grande facilidade. O trabalho num pequeno (infinitesimal) intervalo de tempo \(\left [ t,t+dt \right ]\) é

\(\overrightarrow{F}\left ( t \right )\cdot\overrightarrow{v}dt\) (11)

Note-se que estamos a admitir que a força não é constante. Para obter o trabalho total temos de integrar no tempo. Mas a velocidade do ponto de aplicação, ao contrário da força, é constante, pelo que

\(W=\left [ \int_{t_0}^{t_f}\overrightarrow{F}\left ( t \right )dt \right ]\cdot\overrightarrow{v}\) (12)

Este integral designa-se por impulso, e, por integração direta da segunda lei de Newton, é a variação de momento linear do corpo. Se este estava parado inicialmente e tem velocidade \(\overrightarrow{v}\) no final do processo,

\(W=\overrightarrow{I}\cdot\overrightarrow{v}=m\overrightarrow{v}\cdot\overrightarrow{v}=2E_c\) (13)

A força externa realizou o dobro do trabalho necessário para a variação de energia cinética do corpo. Isto é transferiu o dobro da energia que aparece como energia de translação. Onde está o que resta, que é outro tanto? Ninguém disse nada sobre atrito; não deveria haver conservação de energia?

Essa é uma das lições a tirar deste exemplo. Cuidado com a conservação de energia! Ninguém falou de atrito porque não era necessário. O processo em si, tal como foi descrito, implica dissipação de energia no interior do corpo que é arrastado. Imaginemos, por exemplo, que o corpo é uma cadeia de elos entrelaçados inicialmente enrolada em repouso. Engatamos um elo na extremidade da cadeia e puxamos com velocidade constante. A cadeia desenrola e, nesse processo, cada elo colide com o seguinte. Para que, no final, todos se desloquem com a velocidade de arrastamento, estas colisões são inelásticas e dissipam energia. O que surpreende é que, dadas as condições inicial e final, os pormenores são irrelevantes: a energia dissipada é igual à energia cinética final de translação.

Há um caso em que podemos analisar com mais pormenor este processo, para chegar a esta mesma conclusão.

Barra elástica.

O corpo que vamos arrastar é uma barra elástica, inicialmente em repouso. Impomos numa extremidade uma velocidade constante \(\overrightarrow{v}\). Qual é o movimento da barra?

Tratar a barra como um corpo rígido não serve neste caso. Pensemos na metade de trás da barra. Esta não acelera enquanto não existir uma extensão da metade dianteira que origine uma força elástica. O que vamos ter é uma onda de deformação elástica que se vai propagar da frente para trás na barra. A barra não estará toda em movimento até que essa onda a percorra de uma ponta à outra, ou seja, até que tenha decorrido um tempo \(\Delta t=L/c_s\), em que \(L\) é o comprimento da barra \(c_s\) e a velocidade de propagação de ondas longitudinais (som) (FIGURA 1).

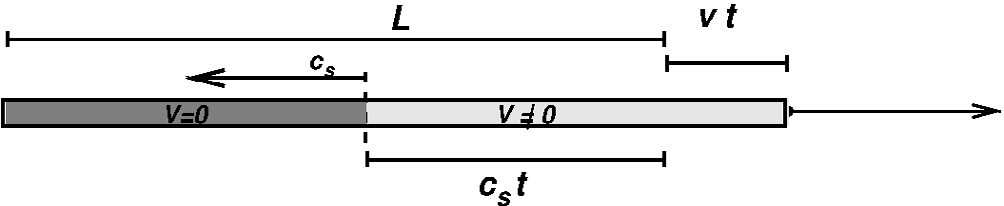
Para resolver este problema temos de escrever as equações de elasticidade do corpo e resolvê- las com as condições dadas: barra inicialmente em repouso e extremidade com velocidade \(\overrightarrow{v}\) para \(t>0\).

A solução é simples e curiosa. Em cada instante há um comprimento \(l\left ( t \right )\) da barra com velocidade \(\overrightarrow{v}\) à frente e uma parte de trás com comprimento \(L-c_st\) parada. Há uma frente de choque (descontinuidade da velocidade) que se desloca para trás na barra à velocidade do som na barra. Esta onda atinge a extremidade traseira da barra passado um tempo \(\Delta t=L/c_s\).

O comprimento da barra, nesse instante, é fácil de calcular: a extremidade traseira da barra ainda está na sua posição inicial e a da frente deslocou-se \(v\Delta t\). A variação de comprimento é

\(\Delta L=v\Delta t=\frac{v}{c_s}L\) (14)

Nesse momento temos uma energia de deformação elástica da barra

\(E_p=\frac{1}{2}k\Delta L^{2}\) (15)

A constante de mola da barra obtém-se da lei de Young (\(E\) módulo de Young e \(A\) área da secção transversal da barra)

\(\frac{F}{A}=E\frac{\Delta L}{L}\) (16)

ou \(F=k\Delta L\), com \(k=EA/L\).

A energia elástica é

\(E_p=\frac{1}{2}\left ( \frac{EA}{L} \right )\Delta L^{2}=\frac{1}{2}\left ( EAL \right )\left ( \frac{v}{c_s} \right )^{2}\) (17)

A velocidade do som é \(c_s=\sqrt{E/\rho}\), em que \(\rho\) é a densidade, e o resultado final é

\(E_p=\frac{1}{2}\left ( \rho AL \right )v^{2}=\frac{1}{2}mv^{2}\) (18)

Neste caso, o trabalho da força externa aparece como variação de energia cinética de translação e como energia de deformação elástica da barra. Posteriormente a barra vai ficar a vibrar com uma energia de oscilação igual à sua energia de translação. A conservação de energia não falha; mas, às vezes, é mais difícil encontrar todos os seus termos do que aplicar a segunda lei!

Conclusão.

O teorema de energia cinética (equação 7) tem validade universal pois pode ser deduzido da segunda lei de Newton. Contudo, é incorreto interpretar o termo \(\overrightarrow{F}\cdot\overrightarrow{\Delta}r\) como sendo o trabalho das forças externas; é apenas o produto escalar da resultante das forças externas pelo deslocamento do centro de massa. Vimos exemplos em que o trabalho externo pode ser maior que este produto ou até ter sinal oposto. O teorema da energia cinética não é uma equação de balanço de energia.

Notas

^a No caso de força variável o primeiro membro da equação 7 é um integral, \(\int \overrightarrow{F}\cdot d\overrightarrow{r}\).