1. Introdução.

As ondas sonoras são vibrações da densidade ou pressão de um meio material (gasoso, líquido ou sólido) que se propagam, a partir de uma fonte, na forma de ondas mecânicas. Ondas de ultrassons são também ondas mecânicas mas com frequência maior que a banda audível para seres humanos. Estas ondas são vibrações mecânicas; longitudinais quando transmitidas através de meios gasosos e líquidos e longitudinais e transversais quando transmitidas através de meios sólidos isotrópicos, de que as ondas sísmicas são exemplo. Propagam-se na forma de ondas de compressão e rarefacção, não podem viajar no vácuo e viajam a uma velocidade especifica do meio, com velocidade maior em meios mais densos.

As ondas de ultrassons possuem propriedades e características únicas, incluindo frequências mais altas do que as ondas sonoras, o que permite diferentes aplicações baseadas na capacidade de resolução e penetração, que varia conforme a frequência utilizada. Possuem densidade energética que lhes permita serem transmitidas a grande distância e produzir calor intenso quando atravessam a matéria e são capazes de gerar vibrações visíveis em líquidos de baixa viscosidade.

Ao propagarem-se através de um meio sofrem reflexão, refração e absorção e, portanto, embora uma parte da energia seja dissipada e espalhada, alguma energia é refletida de volta ao emissor, habitualmente designado por transdutor. As ondas refletidas podem ser detetadas pelo mesmo transdutor e, eventualmente, processadas dando origem á formação de imagens que dependem das características dos meios onde se propagam esses sinais. As imagens formadas a partir de ultrassons são comumente usadas em ultrassonografia para gerar imagens de tecidos e órgãos, sendo um instrumento clínico que pode ajudar o médico a avaliar, diagnosticar e tratar condições de saúde.

Neste artigo são discutidos os princípios de geração de ultrassons e suas propriedades físicas que originam a geração de imagens e apresentam-se alguns exemplos práticos.

2. Geração e propagação de ultrassons.

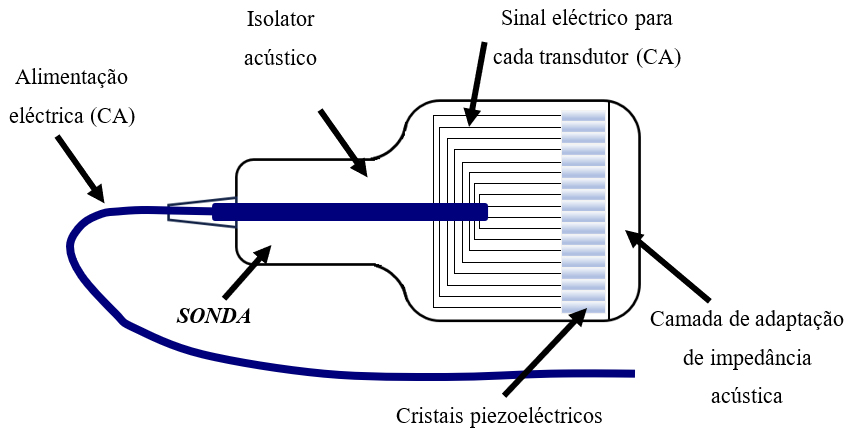
Um sistema emissor de ultrassons consiste num transdutor constituído por cristais piezoelétricos, usualmente Lead Zirconate Titanate (PZT), que vibram quando estimulados por uma tensão elétrica¹, tal como ilustrado na FIGURA 1, sendo essas vibrações transmitidas às partículas vizinhas, dando origem a uma onda mecânica.

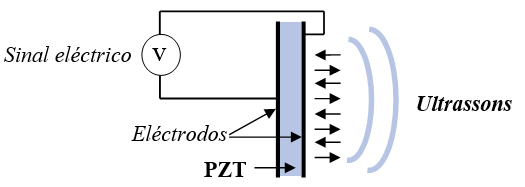
Como resultado dessas vibrações energia é transferida para o meio circundante na forma de energia térmica, mas parte da energia é usada para comprimir e expandir o meio circundante, criando variações locais de pressão. Essas regiões de alta e baixa pressão movem-se como ondas de pressão longitudinais (ondas mecânicas) com a mesma frequência do transdutor. As ondas de ultrassons no ar e na maioria dos fluidos são longitudinais, porque os fluidos têm pequena resistência ao cisalhamento, mas em meios sólidos podem ser longitudinais e transversais.

A FIGURA 2 A) ilustra as variações de pressão ao longo da direção de propagação e o correspondente gráfico dessas variações em função da distância ao transdutor. Durante meio período o transdutor move-se no sentido positivo e desloca as partículas do meio das posições de equilíbrio; no meio período seguinte o transdutor move-se no sentido negativo e as partículas deslocam- se em sentido oposto devido a uma pressão menor. Assim, as partículas oscilam com um movimento harmónico simples em torno de suas posições de equilíbrio, tal como ilustrado na FIGURA 2 B). Note-se que neste exemplo as ondas mecânicas são longitudinais pois estas propagam- se na direção \(x\) e as partículas do meio oscilam (vibram) paralelamente a essa direção.

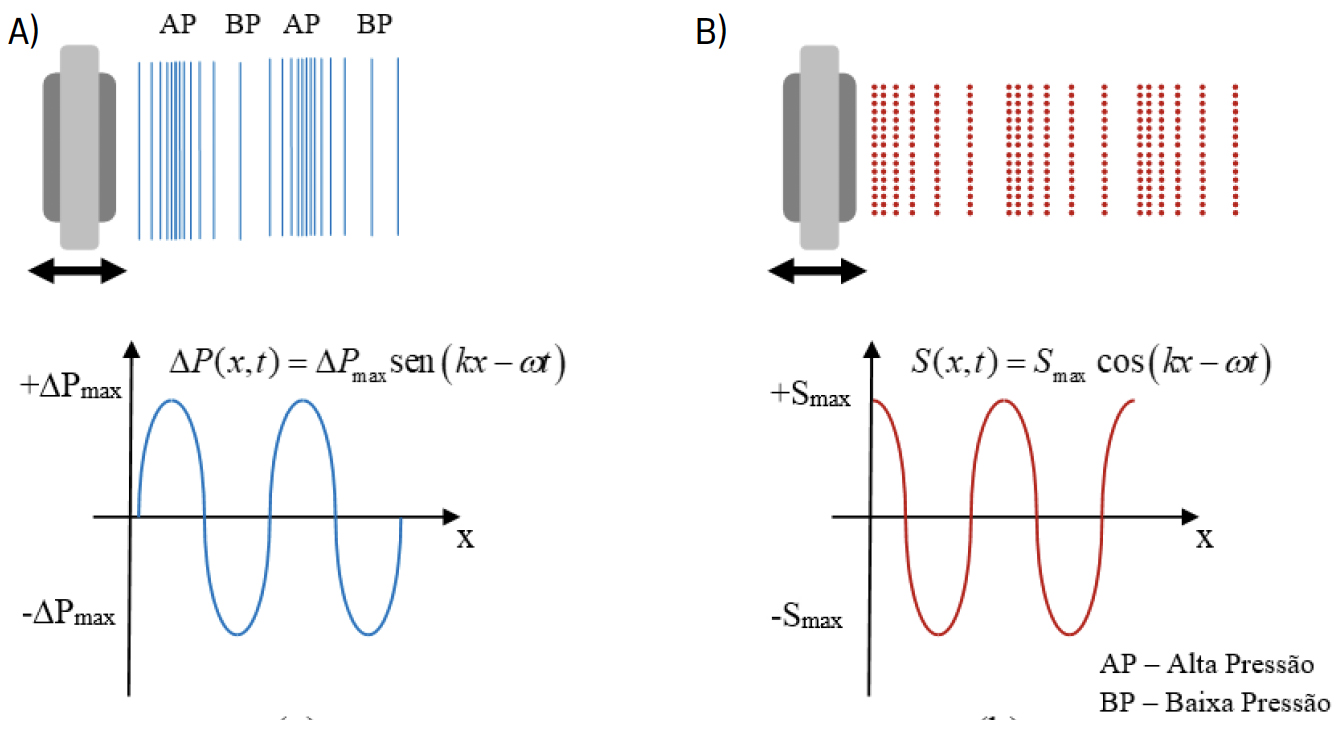
Frequência e comprimento de onda.

Por definição, os ultrassons são ondas sonoras que excedem a frequência audível para seres humanos que vai de 20 Hz a 20 kHz². A unidade Hz (Hertz) ou “ciclos por segundo”, é a unidade de frequência. A periodicidade espacial das ondas é denominada comprimento de onda; é a distância entre pontos com as mesmas características de uma determinada da onda. Essa distância pode ser a que separa pontos de máxima (ou mínima) compressão. A frequência é inversamente proporcional ao comprimento de onda, portanto, quanto maior a frequência, menor será o comprimento de onda:

\(f=\frac{v}{\lambda}\)

em que \(v\) é a velocidade da onda, \/f\) é a frequência e é o comprimento de onda.

3. Interação dos ultrassons com os tecidos.

À medida que uma onda de ultrassons se propaga, encontra diferentes estruturas no seu percurso. A interação resulta em atenuação (diminuição da intensidade da onda) devido à absorção, à reflexão e ao espalhamento, e em refração.

A velocidade com que os ultrassons se propagam depende do meio envolvente. Em tecidos moles, a velocidade média de propagação dos ultrassons é 1540 m/s. A velocidade de propagação também depende da compressibilidade e da densidade de um determinado meio. Estruturas mais densas, como por exemplo ossos, são caracterizados por velocidade de propagação mais elevada.

3.1. Impedância acústica especifica.

Os vários tecidos que a onda de ultrassons encontra no seu percurso possuem diferente massa especifica, \(\rho\), expressa em \(kg.m^{-3}\) no Sistema Internacional (SI), e a impedância acústica especifica, \(z\), que é definida como o quociente entre a pressão sonora e a velocidade de propagação dos ultrassons nos tecidos em estudo:

\(z=\frac{p}{v}\) (1)

que se expressa em rayl no SI: (\(\frac{Pa}{ms^{-1}}=kgm^{-2}s^{-1}=\) rayl), e que também pode ser escrita como o produto da massa especifica pela velocidade de propagação: \(z=\rho.v\) (e no SI vem: \(kg.m^{-3}ms^{-1}=kgm^{-2}s^{-1}=\) rayl, de modo coerente). Como,

\(v=\sqrt{\frac{E}{\rho}}\) (2)

para ondas mecânicas longitudinais vem, \(z=\sqrt{E\rho}\), ou seja, quanto maior o valor do módulo de Young (E) maior é a impedância acústica específica³.

3.2. Reflexão e Refração.

De acordo com a lei de Snell-Descartes quando uma onda eletromagnética passa através de uma interface entre dois materiais com índices de refração diferentes são produzidas ondas refletidas e refratadas. O mesmo princípio pode ser aplicado a ondas de ultrassons. Tal como ilustrado na FIGURA 3 quando uma onda se propaga em dois meios com impedância acústica especifica diferente existem ondas refletidas e refratadas. A Lei de Snell-Descartes descreve a relação entre os ângulos \(\theta_i\), \(\theta_r\) e \(\theta_t\) e as velocidades das ondas, \(v_1\) e \(v_2\) nos meios 1 e 2. Para a reflexão e para a refração tem-se, respetivamente,

\(\theta_i=\theta_r\mathrm{e}\frac{\mathrm{sen}\theta_i}{\mathrm{sen}\theta_t}=\frac{\lambda_1}{\lambda_2}=\frac{v_1}{v_2}\) (3)

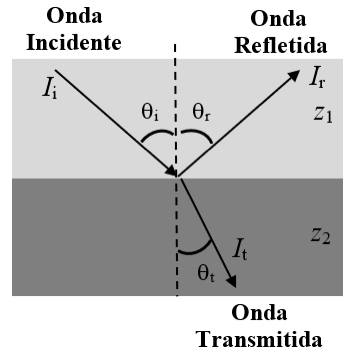
Sendo \(I_i\), \(I_r\) e \(I_t\) as intensidades das ondas incidente, refletida e refratada (expressa em \(Wm^{-2}\)), por conservação de energia, tem-se que \(I_i=I_r+I_t\).

De acordo com as leis de Fresnel quando uma onda eletromagnética passa através de uma interface entre dois materiais com índices de refração diferentes existe uma relação entre \(I_i\), \(I_r\) e \(I_t\). Tal como anteriormente, estas leis podem ser aplicadas a ondas de ultrassons. A relação entre a intensidade da onda incidente e a intensidade das ondas refletida e refratada é dada por,

\(I_{r}=I_{i}\left(\frac{z_{1}\cos\theta_{t}-z_{2}\cos\theta_{i}}{z_{1}\cos\theta_{t}+z_{2}\cos\theta_{i}}\right)^{2}\) e \(I_{t}=I_{i}\left[\frac{4z_{1}z_{2}\cos\theta_{t}\cos\theta_{i}}{\left(z_{1}\cos\theta_{t}+z_{2}\cos\theta_{i}\right)^{2}}\right]\) (4)

Um caso particular é aquele em que a onda incidente é perpendicular á interface, \(\theta_i=0\). Neste caso vem \(\theta_r=0\) e \(\theta_t=0\) e as equações ficam simplificadas, sendo as intensidades refletida e transmitida dadas agora por:

\(I_r=I_i\left(\frac{z_1-z_2}{z_1+z_2}\right)^2\) e \(I_{t}=I_{i}\left[\frac{4z_{1}z_{2}}{\left(z_{1}+z_{2}\right)^{2}}\right]\) (5)

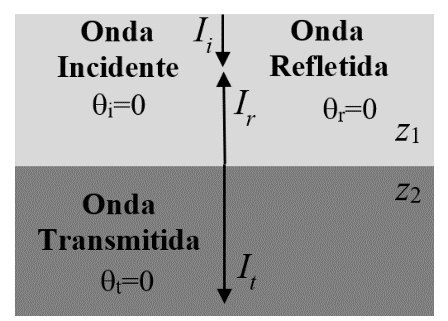
Tecidos com elevado valor da impedância acústica especifica refletem fortemente a onda incidente (eco forte) e uma fração da intensidade presente na onda incidente será refletida na interface entre os dois tecidos. Materiais como ossos tem grande impedância acústica especifica e podem refletir uma fração apreciável da intensidade da onda incidente. Materiais com impedância acústica especifica semelhante à do meio de onde provém a onda incidente permitem que a onda se propague sem reflexão significante, originando uma onda refratada com intensidade significativa.

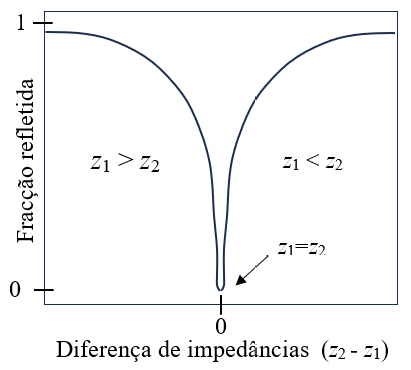
Na FIGURA 5 ilustra-se a intensidade refletida, normalizada á intensidade da onda incidente, na superfície de separação entre dois meios com impedância acústica especifica \(z_1\) e \(z_2\), em função da diferença \(z_2-z_1\). Note-se que quando \(z_2=z_1\) a intensidade da onda refletida é nula e, portanto não haverá uma onda refletida de volta ao transdutor que originou essa onda e, assim, essa superfície de separação não seria visualizada num exame medico.

Exemplos práticos.

1. A impedância acústica especifica do ar é \(z_1=0,0004286\times 10^6\) rayl e a da gordura é \(z_2=1,42\times 10^6\) rayl. Para uma onda de ultrassons que atinge a superfície de separação ar/ gordura perpendicularmente á superfície, o valor da intensidade refletida é:

\(\frac{I_r}{I_i}=\left(\frac{z_1-z_2}{z_1+z_2}\right)^2=\left(\frac{0,0004286\times10^6-1,42\times^6}{0,0004286\times10^6+1,42\times^6}\right)=0,999=99,9\)

ou seja, quase toda a energia é refletida quando as impedâncias acústicas são muito diferentes, não ficando energia disponível para analisar outras estruturas mais profundas no organismo.

2. A impedância acústica especifica do fígado é \(z_1=1,64\times 10^6\) rayl e a do sangue é \(z_2=1,60\times 10^6\) rayl. Para uma onda de ultrassons que atinge a superfície de separação entre o fígado e um vaso sanguíneo, perpendicularmente á superfície, o valor da intensidade transmitida é:

\(\frac{I_{t}}{I_{i}}=\left[\frac{4z_{1}z_{2}}{\left(z_{1}+z_{2}\right)^{2}}\right]=\frac{4\times1,64\times10^{6}\times1,60\times10^{6}}{\left(1,64\times10^{6}+1,60\times10^{6}\right)^{2}}=0,999=99,9\)

ou seja, muito pouca energia é refletida quando as impedâncias acústicas são idênticas e, portanto, a intensidade da onda refletida é pequena; dificultando a informação se obtém acerca dessa superfície.

3.3 Absorção.

A intensidade das ondas de ultrassons diminui por absorção quando se propagam nos tecidos, libertando a energia sob a forma de calor, sendo essa dependência exponencial:

\(I\left ( x \right )=I_0\textrm{exp}\left ( -kx \right )\) (6)

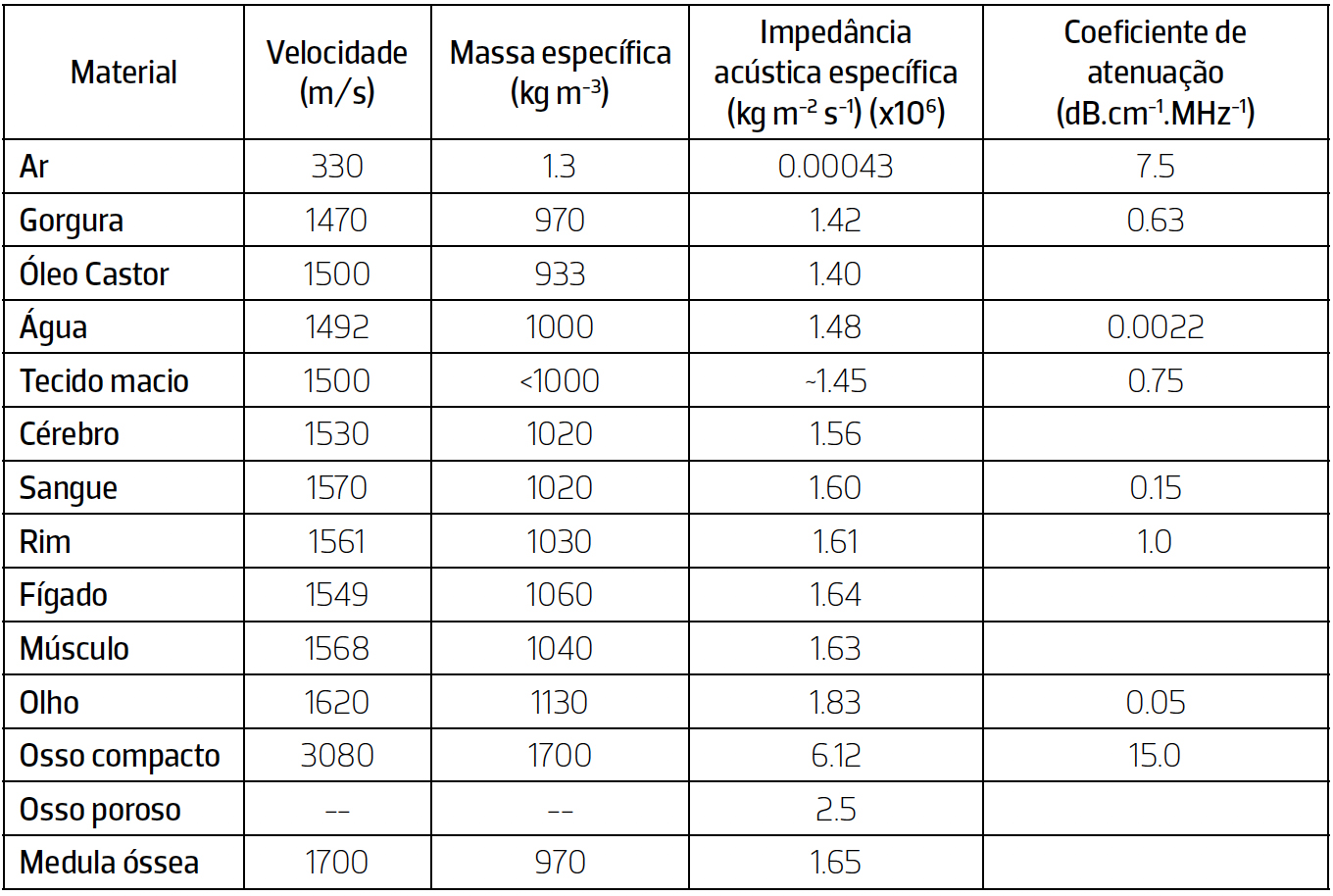
em que \(I_0\) é a intensidade da onda incidente, é a distância percorrida e é o coeficiente de absorção que aumenta, aproximadamente, com o quadrado da frequência e é expresso em \(m^{-1}\). No entanto, habitualmente na literatura a absorção é quantificada em \(dB.cm^{-1}.MHz^{-1}\). Na TABELA 1 encontra-se o valor do coeficiente de atenuação para vários tecidos orgânicos⁴.

Assim, como quanto maior é a frequência dos ultrassons maior é a atenuação, a profundidade a que é necessário analisar um ser vivo (humano ou animal) determina a ordem de grandeza do frequências utilizadas. A FIGURA 6 ilustra, de modo aproximado, a profundidade de penetração a 50%, que é a profundidade para a qual a intensidade passa a metade do seu valor inicial (note-se que as ondas têm de percorrer o dobro dessa distância – percurso de ida e volta entre a sonda emissora e receptora e a superfície que reflete os ultrassons).

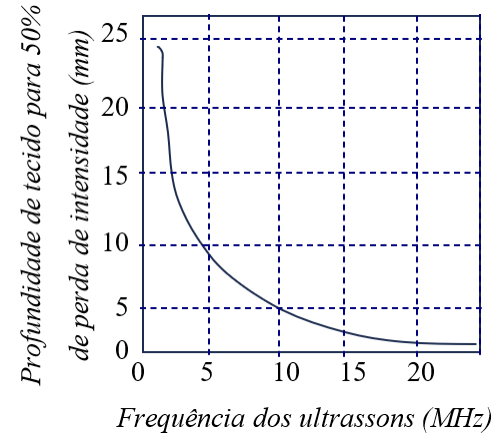
Assim, a profundidade a 50% a 10 MHz é de ~0,5 cm e a 2 MHz é de ~2,4 cm. Enquanto ultrassons com frequências entre 7 e 15 MHz são utilizados para visualizar estruturas superficiais, frequências entre 2 e 3 MHz são usadas para analisar detalhes mais profundos.

4. Formação de imagem.

Em medicina os ultrassons são transmitidos através dos tecidos do corpo enquanto os sinais refletidos de volta ao transdutor (ecos) são processados para gerar imagens de estruturas internas em tempo real.

4.1. Fundamentos.

Uma sonda de ultrassons, ilustrada FIGURA 7, é constituída por vários transdutores (cristais piezoelétricos), responsáveis pela geração e deteção de ondas de ultrassons, sendo o seu número dependente da aplicação (tipo de tecidos a analisar); algumas sondas podem ter 128 elementos transdutores dispostos em arranjos lineares ou curvilíneos^{5, 6}. No entanto, já foram apresentadas sondas com transdutores de cristal único para aplicações biomédicas, incluindo imagens oculares, intravasculares e medição de fluxo sanguíneo⁷.

A escolha do material piezoelétrico, como o PZT, é crucial para a otimização da sonda, pois afecta a eficiência, a pressão sonora, a intensidade sonora e a qualidade da imagem obtida a partir das ondas de ultrassons emitidas e recebidas⁸. Uma visão geral da investigação e desenvolvimento recente em tecnologias de transdutores de ultrassons, utilizando uma variedade de diferentes materiais e configurações⁹.

Um sinal elétrico (tensão elétrica) é convertido pelos transdutores piezoelétricos em energia mecânica e a onda de ultrassons associada é enviada para os tecidos. Esses mesmos transdutores piezoelétricos recebem os ecos (onda de ultrassons refletida) vindos dos tecidos e convertem- nos em sinais elétricos, que são processados por um computador para criar uma imagem. Concretamente, cada transdutor piezoelétrico é excitado periodicamente com impulsos elétricos de curta duração provenientes de um circuito eletrónico exterior, dando origem a impulsos de ultrassons que se propagam nos tecidos adjacentes. O sistema eletrónico de controle mede o tempo que um impulso leva a voltar para trás depois de refletido numa superfície entre constituintes de órgãos (tempo de voo). Assim, a profundidade à qual o impulso foi refletido pode ser calculada se a velocidade da onda de ultrassons no tecido for conhecida. Por outro lado, a intensidade da onda refletida pode ser codificada em diferentes tons de cinza e visualizada no monitor do equipamento de controlo. Portanto, a intensidade da onda refletida e o tempo de retorno do eco em direção ao transdutor, são a base da formação de imagem em ultrassonografia.

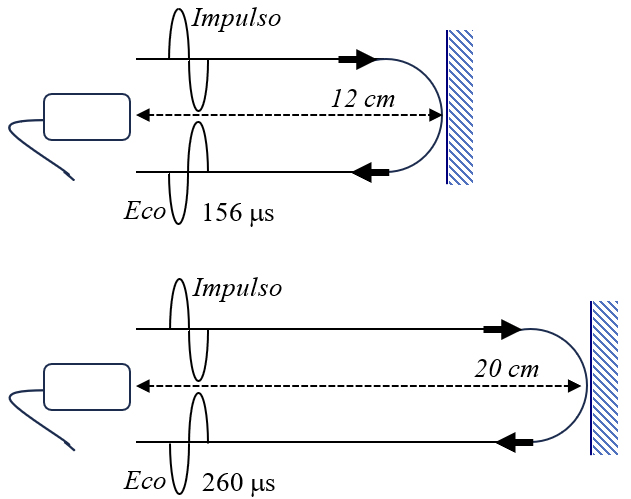
A FIGURA 8 ilustra duas situações em que os impulsos são refletidos em duas superfícies situadas a diferentes distâncias da sonda emissora e receptora de ultrassons. Se o equipamento medir os tempos de voo de 156 e 260 μs e, assumindo que a velocidade de propagação dos ultrassons é 1540 m/s, pode calcular-se o valor da profundidade dessas superfícies, obtendo- se os valores de 12 e 20 cm, respetivamente. Nestes cálculos não se tem em consideração a eventual diferença de constituição do tecidos através do quais se propagam as ondas e a consequente diferença de velocidade. Assume-se que a velocidade é 1540 m/s em todos os tecidos o que torna a estimativa de distâncias difícil e conduz á distorção de contornos de constituintes dos órgãos¹⁰.

Ondas de ultrassons com frequências mais elevadas são facilmente absorvidas por estruturas superficiais e não se propagam em profundidade, enquanto que ondas com frequências mais baixas têm maior comprimentos de onda e são capazes de penetrar até estruturas mais profundas. Por outro lado, ultrassons com frequências mais altas permitem melhor resolução espacial; na faixa de 5 a 15 MHz são usados para identificar estruturas superficiais, enquanto que ultrassons com frequências inferiores, na faixa de 2 a 5 MHz, são usadas para estudar estruturas mais profundas. Transdutores de frequência mais alta são usados para ecocardiografia trans-esofágica e estruturas superficiais, enquanto transdutores de frequências inferiores são usados para ecocardiografia transtorácica.

4.2 Resolução da imagem.

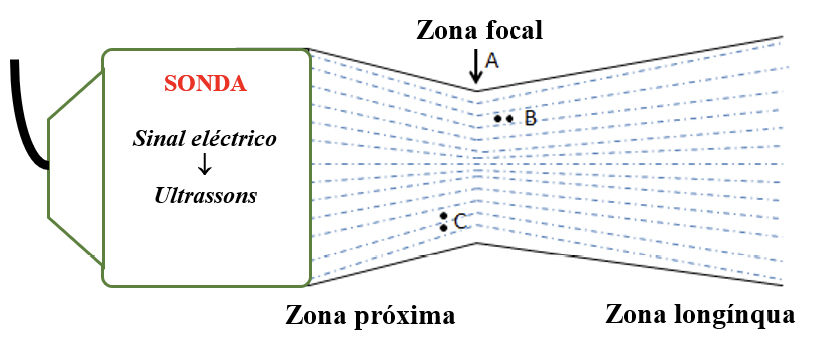
A espessura dos cristais piezoelétricos determina a frequência dos ultrassons que por sua vez determina a localização da zona próxima e da zona longínqua do foco. Define-se resolução da imagem como sendo a menor distância entre dois pontos que podem ainda ser discriminados. Tal como ilustrado na FIGURA 9 é melhor na zona focal (A), onde o feixe de ondas de ultrassons são mais estreitos. Pode-se distinguir resolução lateral de resolução axial.

A resolução lateral (C) é a capacidade do sistema para discriminar dois objectos situados num plano perpendicular ao feixe. é melhor na zona focal. Depende da distância entre os cristais individuais e diminui à medida que o feixe começa a divergir e é atenuado pelos tecidos. A resolução axial (B) refere-se à capacidade do sistema para diferenciar objectos situados numa linha paralela ao eixo da onda; depende da duração dos impulsos e da frequência, sendo melhor para frequências maiores.

5. Efeito Doppler.

5.1. Fundamentos.

Se uma onda de ultrassons e o correspondente detetor (transdutor) possuírem movimento relativo a frequência e o comprimento de onda medidos variam. Este fenómeno designa-se efeito de Doppler, dado que foi Christian Doppler o físico que descreveu o fenómeno em 1842. Consiste na mudança de frequência de uma onda em relação a um observador que se está a deslocar em relação à fonte que origina a onda.

Considere-se por simplificação que existe um movimento relativo rectilíneo e uniforme, tal como ilustrado na FIGURA 10. Suponhamos que em \(t=0\) a fonte está no ponto \(F\) e detetor está no ponto \(D\) e seja \(\bar{v}\) a velocidade da onda \(\bar{v_f}\), a velocidade da fonte e \(\bar{v_D}\) a velocidade do detetor.

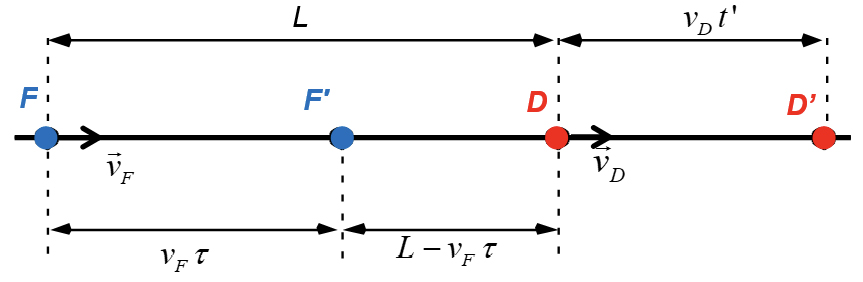
Em \(t=0\) a fonte emite uma onda que chega ao detetor no instante \/t\); o detetor percorreu a distância \(v_D.t\) e a onda percorreu a distância \(L+v_D.t\). Sendo \(v\) a velocidade da onda tem-se que \(v.t=L+v_D.t\) e, então, \(t=\frac{L}{v-v_0}\). Num instante posterior, \/\tau\), a fonte estará em \(F^{\prime}\left(\overline{FF^{\prime}}=v_{F}.\tau\right)\) e a onda alcança o detetor (na posição \(D'\)) num instante posterior, \(t'\). A distância percorrida pela onda é \(L-v_{F}+v_{D}t^{\prime}=v.\left(t^{\prime}-\tau\right)\), ou seja,

\(t^{\prime}=\frac{L+(v-v_F)\tau}{v-v_D}\)

O intervalo de tempo medido pelo detetor entre as ondas emitidas pela fonte quando em \(F\) e \(F'\) é,

\(\tau^{\prime}=t^{\prime}-t=\frac{v-v_F}{v-v_D}\tau\)

Por outro lado, o número de ondas emitidas pela fonte enquanto viaja de \(F\) para \(F'\) é, \(N=f.\tau\), que deve ser igual ao número de ondas medidas pelo detetor no intervalo \(\tau'\), \(N=f'.\tau'\); logo, \(f.\tau=f'.\tau'\) e, então, a relação entre a frequência medida pelo detetor e a frequência da fonte é

\(f^{\prime}=f.\frac{v-v_D}{v-v_F}\)

5.1. Ecocardiograma Doppler

No contexto da notação anterior, a sonda é detetora dos ultrassons (sendo evidentemente também a fonte dos impulsos de ultrassons) e os glóbulos vermelhos, em movimento nos vasos sanguíneos, refletem o feixe de ultrassons, que desempenham o papel de emissor (fonte) móvel.

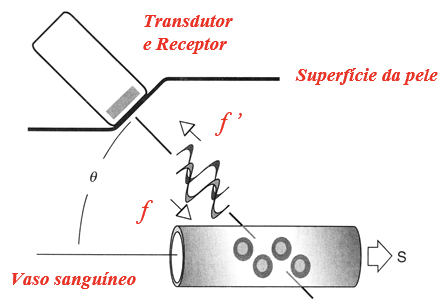
O efeito Doppler originou o desenvolvimento de equipamentos que permitem a realização de ecocardiograma Doppler (ou Ecocardiografia), que consiste na medição da velocidade do sangue nos vasos sanguíneos e a velocidade de deslocamento de estruturas móveis do organismo (por exemplo as válvulas cardíacas) utilizando ultrassons entre 2 e 10 MHz.

A técnica permite avaliar pacientes com sopro cardíaco, sintomas de palpitação, síncope, falta de ar, dor torácica, doenças do músculo cardíaco (infarto do miocárdio e miocardiopatias), insuficiência cardíaca, doenças das valvas, anomalias congénitas, entre outras. É possível obter- se imagens estáticas ou dinâmicas do músculo e das válvulas cardíacas, podendo-se identificar a direção e velocidade do fluxo sanguíneo no interior das cavidades.

6. Conclusão.

A ultrassonografia é uma tecnologia médica essencial que utiliza ondas sonoras de alta frequência para criar imagens de órgãos e tecidos internos. Este método diagnóstico é seguro, não invasivo e não utiliza radiação ionizante, tornando-o uma escolha preferencial para monitorar a saúde de pessoas e animais.

A compreensão dos princípios físicos das ondas de ultrassons é crucial para otimizar a qualidade das imagens e interpretá-las correctamente. O conhecimento sobre a interação das ondas de ultrassons com diferentes tecidos e a identificação de artefactos de imagem são fundamentais para um diagnóstico preciso. A ultrassonografia continua a evoluir, com avanços tecnológicos que melhoram a resolução das imagens e expandem suas aplicações na medicina.