Tudo começou na década de 1980, quando alguns dos maiores físicos e teóricos sonharam com a possibilidade de usar as leis estranhas e fascinantes da física quântica para criar uma nova forma de computação. Um deles foi Richard Feynman, que percebeu que a física quântica poderia tornar os computadores muito mais poderosos do que os clássicos, capazes de simular formas que nunca imaginamos.

Assim nasceu a ideia de um computador quântico – uma máquina que utiliza partículas em sobreposições e entrelaçamento para realizar cálculos. Nos anos 2000, esse sonho começou a ganhar forma. Os cientistas criaram os primeiros qubits físicos, controlando iões, partículas supercondutoras ou átomos, e realizando experiências que mostravam que era possível manipular esses pequenos “blocos” de informação de maneiras novas e impressionantes.

No entanto, esses primeiros dispositivos ainda eram frágeis, com poucos qubits e muita instabilidade. Então, veio o grande passo em frente: em 2019, a equipa da Google anunciou uma conquista histórica. Com o seu computador quântico, chamado Sycamore, realizaram uma tarefa que, dizem, somente um computador quântico poderia fazer em poucos minutos – algo que levaria milhares de anos para um supercomputador convencional. Chamaram-lhe “supremacia quântica”, um momento que marcou o início de uma nova era.

Desde então, países e empresas em quase todo o mundo aceleraram os seus esforços. A IBM disponibilizou livremente uma plataforma na internet chamada IBM Quantum, onde qualquer pessoa pode experimentar e aprender. A China avançou com os seus próprios computadores e até testou uma rede de comunicação quântica via satélite, considerada um grande avanço estratégico. Países da Europa investiram milhões para criar centros de investigação e desenvolver tecnologia. Hoje, os cientistas trabalham para aperfeiçoar esses dispositivos. Tentam fazer com que eles fiquem mais estáveis, mais rápidos e mais capazes de resolver problemas reais, de otimização, simulação de moléculas complexas e muitos outros.

A promessa é que, num futuro próximo, computadores quânticos com milhares ou milhões de qubits possam revolucionar setores inteiros da ciência, tecnologia e segurança. A história da computação quântica é uma história de coragem, imaginação e competição mundial, movida pelo sonho de transformar o mundo com o poder das leis mais profundas do universo. Se cada avanço é uma pequena conquista, o que nos espera no horizonte ainda é incerto – mas certamente empolgante!

Se o leitor estiver interessado em entrar neste mundo fascinante, certamente que, primeiramente, colocará a pergunta seguinte:

O que preciso de saber sobre mecânica quântica (MQ)?

Não muito!... Pelo menos neste nível introdutório. Até porque este artigo é um mero aperitivo para um assunto que é complexo e continua a ser objecto de investigação recente. Mas para compreender as ideias principais da Computação Quântica (CQ), não precisamos de muito “background” em mecânica quântica.

Comecemos então com o indispensável para que, após esta introdução, possamos entender um exemplo de algoritmo quântico – o algoritmo de Grover, que será descrito na seção final deste artigo.

Sobreposições quânticas. Bits e qubits.

Nos computadores clássicos, o bit é a unidade de informação mais básica – representa um estado lógico com um de dois valores possíveis. Esses valores são, em geral, representados como “0” ou “1”, mas outras representações como verdadeiro/falso, sim/não, ligado/desligado ou +/−, também são muito usadas.

Em computadores quânticos, os valores 0 e 1 são substituídos, respetivamente, pelos vetores \(\left|0\right\rangle\) e \(\left|1\right\rangle\), usando a chamada notação de Dirac, que é usual em mecânica quântica. O termo bit é substituído por qubit, ou seja, bit quântico. A diferença radical para o bit clássico, é que o bit quântico, ou qubit, pode ser uma sobreposição (ou combinação linear) dos vetores e , ou seja, pode ser da forma:

qubit \(\to|q\rangle=\alpha|0\rangle+\beta|1\rangle,\quad\alpha,\beta\in\mathbb{C}:|\alpha|^2+|\beta|^2=1\) (1)

O qubit \(\left|q\right\rangle\) é pois uma sobreposição linear dos vetores \(\left|0\right\rangle\) e \(\left|1\right\rangle\), com amplitudes complexas \(\alpha\) e \(\beta\), tais que \(\left|\alpha\right|^2+\left|\beta\right|^2=1\). Portanto, \(\left|q\right\rangle\) é um vetor de um espaço vetorial complexo 2-dimensional, onde \(\{|0\rangle,|1\rangle\}\) formam uma base ortonormada, chamada a base computacional. Note que o estado \(\left|0\right\rangle\) não é o vetor nulo, mas simplesmente o primeiro vetor da base.

As representações matriciais dos vetores \(\left|0\right\rangle\) e \(\left|1\right\rangle\) são geralmente dadas por

\(|0\rangle={\binom{0}{1}},\quad|1\rangle={\binom{1}{0}}\in\mathbb{C}^2\) (2)

de tal forma que o qubit \(|q\rangle=\alpha|0\rangle+\beta|1\rangle\) pode ser escrito na forma

\(|q\rangle=\alpha{\binom{1}{0}}+\beta{\binom{0}{1}}={\binom{\alpha}{\beta}}\in\mathbb{C}^2\)

Em mecânica quântica, os vetores são sistematicamente chamados estados, designação que usaremos de aqui em diante.

Medição.

A interpretação física da sobreposição \(|q\rangle=\alpha|0\rangle+\beta|1\rangle\) é a seguinte: o estado \(\left|q\right\rangle\) coexiste simultaneamente em dois estados, \(\left|0\right\rangle\) e \(\left|1\right\rangle\), bem como em qualquer sobreposição destes. O estado \(|q\rangle=\alpha|0\rangle+\beta|1\rangle\) , pode armazenar uma grande quantidade de informação nos seus coeficientes \(\alpha\) e \(\beta\). No entanto, esta informação “vive” no nível quântico, que é microscópico (à escala de Planck). Para extrair informação clássica da informação quântica, temos que medir o qubit .

A mecânica quântica diz-nos que o processo de medição perturba inevitavelmente o estado do qubit, produzindo um colapso não determinístico de \(|q\rangle=\alpha|0\rangle+\beta|1\rangle\), ou no estado \(\left|0\right\rangle\), com probabilidade \(\left|\alpha\right|^2\), ou no estado \(\left|1\right\rangle\), com probabilidade \(|\beta|^2.

\(|q\rangle=\alpha|0\rangle+\beta|1\rangle\xrightarrow{\mathrm{medicao}} \begin{cases} |0\rangle & & \text{probabilidade}=|\alpha \\ |1\rangle & & \text{probabilidade}=|\beta| & & \end{cases}\)

Produto de qubits. Multi-qubits.

Os qubits podem ser multiplicados (formalmente, através do chamado produto tensorial) para formar multi-qubits ou \(n\)-qubits, onde é um inteiro \(\geq2\).

Assim, por exemplo, os qubits e \(\left|{0}\right\rangle\), \(\left|{1}\right\rangle\) quando multiplicados formam o 2-qubit

\( \left | 0 \right > \left | 1 \right >\overset{\underset{\mathrm{def}}{}}{=} \left | 01 \right >\in \mathbb{C}^4\)

Mais geralmente, os qubits \(|q_1\rangle,|q_2\rangle\cdots,|q_n\rangle\in\mathbb{C}^2\), podem ser combinados para formar o \(n\)-qubit:

\(|Q\rangle=|q_1q_2\cdots q_n\rangle\in\mathbb{C}^{2n}\)

Observe que este produto de qubits é não comutativo e, por isso, a ordem deve ser preservada.

Entrelaçamento Quântico (EQ).

Quando consideramos computadores quânticos com (pelo menos) 2-qubits, um fenómeno muito interessante e surpreendente pode ocorrer. Consideremos então dois 1-qubits, o primeiro no estado.

\(|q_1\rangle=a|0\rangle+b|1\rangle\)

e o segundo no estado

\(|q_2\rangle=c|0\rangle+d|1\rangle\)

O estado composto

\(\begin{aligned} \left|{Q}\right\rangle & =|q_1q_2\rangle \\ & =|(a|0\rangle+b|1\rangle)(c|0\rangle+d|1\rangle)\rangle \\ & =ac|00\rangle+ad|01\rangle+bc|10\rangle+bd|11\rangle \end{aligned}\)

é um 2-qubit, obtido pelo produto (tensorial) dos dois 1-qubits \(\left|q_{1}\right\rangle\) e \(\left|q_{2}\right\rangle\).

Como se viu antes, um 2-qubit genérico é do tipo

\(|Q\rangle=\alpha|00\rangle+\beta|01\rangle+\gamma|10\rangle+\delta|11\rangle\) (3)

e será da forma (3), se e só se

\(\alpha=ac,\quad\beta=ad,\quad\gamma=bc,\quad\delta=bd\)

\(\alpha\delta=\beta\gamma\)

Se esta condição é violada o 2-qubit não é separável (ou factorizável) como produto de dois 1-qubits.

Concluindo: um 2-qubit não é necessariamente o produto (tensorial) de dois 1-qubits.

Por exemplo, o estado

\(|B_{00}\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}}\) (4)

é um estado válido para um computador quântico de 2-qubits, embora não possa ser escrito como um produto de dois 1-qubits (verifique).

Estes estados, que não são produto de dois ou mais 1-qubits, são chamados de estados entrelaçados, e este fenómeno é designado por Entrelaçamento Quântico.

O estado (4), \(|B_{00}\rangle\) pertence à classe especial de estados entrelaçados, conhecidos como estados de Bell. Os outros estados de Bell são

\(|B_{01}\rangle=\frac{|01\rangle+|10\rangle}{\sqrt{2}},\quad|B_{10}\rangle=\frac{|00\rangle-|11\rangle}{\sqrt{2}},\quad|B_{11}\rangle=\frac{|01\rangle-|10\rangle}{\sqrt{2}},\) (5)

Interpretação: Algumas partículas (por exemplo, eletrões) têm uma propriedade chamada spin, que só pode tomar dois valores (quando medidos numa determinada direcção): spin Up, que representamos por \(\left|1\right\rangle\) e spin Down, que representamos por \(\left|0\right\rangle\).

Suponhamos agora que Alice e Bob têm, cada um, o seu eletrão, e que, por um processo físico, quando estavam juntos, esses eletrões foram postos no estado entrelaçado

\(|B_{01}\rangle=\frac{|0_A1_B\rangle+|1_A0_B\rangle}{\sqrt{2}}\)

Os índices \(A\) e \(B\) indicam a quem pertence o eletrão: se a Alice ou se a Bob.

Agora Alice e Bob separam-se um do outro para duas galáxias muito distantes. Se então Alice mede o spin de seu eletrão, e vê que ele é spin Up, instantaneamente fica a saber que o spin do eletrão de Bob é, com certeza absoluta, spin Down, sem ter que o medir. Essa determinação instantanea ocorre, mesmo que os eletrões estejam separados por grandes distâncias. Os dois eletrões têm uma correlação perfeita, instantanea e à distância!

Os estados entrelaçados desempenham um papel essencial na computação quântica. Os computadores quânticos que não usam Entrelaçamento Quântico não podem ser exponencialmente mais rápidos do que os clássicos.

Operadores quânticos.

Num computador quântico, as informações são processadas usando operadores lineares. Vamos descrever apenas os que vamos usar na secção final deste artigo.

Operador X.

É a generalização do operador NOT clásico, que inverte o valor do bit: \(0\to 1\) e \(1\to 0\). O operador \(X\) é o operador unitário definido por:

\(X|0\rangle=|1\rangle,\quad X|1\rangle=|0\rangle\)

Mais geralmente:

\(X(\alpha|0\rangle+\beta|1\rangle)=\alpha X|0\rangle+\beta X|1\rangle=\alpha|1\rangle+\beta|0\rangle\)

Operador de Hadamard H.

No espaço \(\mathbb{C}^{2}\) dos 1-qubits, é definido na base computacional por:

\(H|0\rangle=\frac{|0\rangle+|1\rangle}{\sqrt{2}}\) e \(H|1\rangle=\frac{|0\rangle-|1\rangle}{\sqrt{2}}\) (6)

Se a entrada for \(\left|0\right\rangle\) (ou \(\left|1\right\rangle\)), \(H\) cria uma sobreposição de estados de igual amplitude. Esta é uma situação geral, válida para \(n\)-qubits, \(n\geq2\).

Por exemplo, \(H\) aplicado a \(\left|00\right\rangle\) dá (por definição):

\(\begin{aligned} H|00\rangle & \overset{\underset{\mathrm{def}}{}}{=}H|0\rangle H|0\rangle \\ & =\left(\frac{|0\rangle+|1\rangle}{\sqrt{2}}\right)\left(\frac{|0\rangle+|1\rangle}{\sqrt{2}}\right) \\ & =\frac{1}{2}(|00\rangle+|01\rangle+|10\rangle+|11\rangle) \\ & =\frac{1}{2}(|0\rangle+|1\rangle+|2\rangle+|3\rangle) \end{aligned}\) (em notação decimal) (7)

O resultado é pois uma sobreposição de todos os estados da base computacional do espaço \(\mathbb{C}^4\) dos 2-qubits, com amplitudes iguais.

Mais geralmente, o operador de Hadamard aplicado ao \(n\)-qubit \(|0\rangle^n \overset{\underset{\mathrm{def}}{}}{=} |0\cdots0\rangle\) é

\(\begin{aligned} H|0\cdots0\rangle & \overset{\underset{\mathrm{def}}{}}{=} H|0\rangle\cdots H|0\rangle \\ & =\left(\frac{|0\rangle+|1\rangle}{\sqrt{2}}\right)\cdots\left(\frac{|0\rangle+|1\rangle}{\sqrt{2}}\right) \\ & =\frac{1}{\sqrt{2^n}}\sum_{Q\in\{0,1\}^n}|Q\rangle \\ & =\frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}|x\rangle \end{aligned}\) (8) (em notação decimal) (9)

Assim, \(H|0\cdots0\rangle\) produz uma sobreposição igualmente ponderada de todos os estados da base computacional em \(\mathbb{C}^{2n}\) – o espaço dos \(n\)-qubits. Este estado é útil para aplicar paralelismo quântico, como veremos adiante.

O operador de Hadamard é involutivo: \(HH=I\). Portanto, se o aplicarmos a \(H|x\rangle\) obtemos

\(H(H|x\rangle)=|x\rangle\) (10)

Aqui, \(H\) pode ser considerado como um descodificador das informações sobre o valor de \(x\), que, anteriormente, tinham sido codificadas nas fases.

E para já, é oque precisamos! Depois desta introdução supersimplificada aos conceitos principais da mecânica quântica, é agora a altura de os usar no desenvolvimento de um algoritmo quântico. Vamos lá, então!

Algoritmo de Grover. Procurar uma agulha num palheiro.

Imagine que o leitor tem um armazém gigante com \(N\) palhinhas (o palheiro), uma das quais é metálica (a agulha). \(N\) pode ser muito grande.

Para encontrar esta “agulha” o leitor pode seguir o método seguinte, chamado busca sequencial: pega numa palhinha. Se ela fôr metálica, pára o pocesso (o objetivo foi alcançado). Caso contrário, pega numa segunda palhinha (diferente da primeira) – se ela fôr metálica pára o pocesso. Caso contrário, pega numa terceira, e assim sucessivamente, até encontrar a “agulha”.

Quantas tentativas são necessárias? O número de tentativas que fazemos até descobrir a “agulha”, varia entre 1 (sorte pura) e \(N\)−1 (azar puro). Se \(N\)=300.000.000 de palhinhas, vamos ver que existe um algoritmo quântico (algoritmo de Grover) que permite encontrar a “agulha” em cerca de 17.321 passos, em média. Se cada tentativa demorar um segundo, terminaremos em cerca de cinco horas.

Classicamente, para encontrar a “agulha”, por busca sequencial, no conjunto completo de 300 milhões de palhinhas, ao mesmo ritmo de uma tentativa por segundo, levaria, em média, cerca de 43 anos, com o horário usual de trabalho!

Como é que conseguimos um aumento tão drástico de eficiência? Grosso modo, aplicando um “método mágico” que permite “ver” ou “testar” muitas palhinhas ao mesmo tempo, usando uma técnica especial que explora as leis da física quântica!

Como funciona este “método mágico”? Em termos muito simplistas, ele coloca todas as palhinhas numa “sobreposição quântica”, e consegue, efetivamente, testar todas ao mesmo tempo, atribuindo a cada uma uma mesma probabilidade (um número entre 0 e 1) de ser a “agulha”!

Depois, usa um truque para “amplificar” automaticamente apenas a probabilidade associada à palhinha metálica (a “agulha”), que é a resposta certa, e, claro, diminuindo as probabilidade das restantes, já que a soma de todas as probabilidade deve ser sempre igual a 1.

Com esse truque, o “método mágico” consegue identificar a “agulha” em muito menos tentativas do que na busca sequencial clássica, acima descrita. Por exemplo, se tivermos 1 milhão de palhinhas, na pior das hipóteses temos que fazer 1 milhão de tentativas. Mas se usarmos um computador quântico, esse número desce para mil apenas – a raíz quadrada de 1 milhão!

Há pois uma mudança drástica de paradigma. Agora a computação quântica usa propriedades especiais (sobreposição, entrelaçamento) que permitem que milhões de possibilidades sejam testadas ao mesmo tempo. Depois, um truque (reflexão de amplitude) faz com que a resposta certa seja a muito mais provável de sair no teste (medição).

Esta é uma mudança revolucionária – existem problemas que seriam impossíveis de resolver com computadores tradicionais, em tempo útil, mas que podem ser resolvidos com computadores quânticos, usando esse “poder de explorar múltiplas possibilidades ao mesmo tempo”.

Em que consiste o “método mágico”?

Em termos simplistas, o “método mágico” faz o seguinte:

1. Rotulamos todas as palhinhas, usando os números

\(x\in\Sigma=\{0,1,\cdots,N-1\}\)

Não existe qualquer ordem ou estrutura nesta rotulagem, porque as palhinhas são todas iguais a olho nu, mesmo a metálica.

Seja a \(a\in\Sigma\) o rótulo (desconhecido) da agulha.

O nosso objetivo é descobrir o rótulo \(a\in\Sigma\) (desconhecido) da agulha, desenvolvendo um algoritmo que comece com um estado de sobreposição uniforme (com amplitudes iguais para todos os estados de base) e depois manipule as amplitudes para aumentar a amplitude associada ao estado correspondente à agulha.

Como fazemos isto?

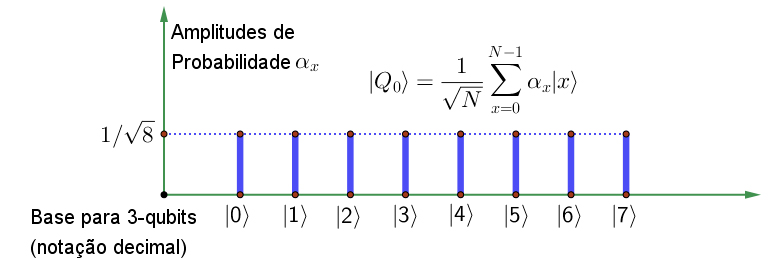
2. Começamos por pôr todas as palhinhas num único estado de sobreposição (FIGURA 2):

\(|Q_0\rangle=\sum_{x=0}^{N-1}\alpha_x|x\rangle,\quad\alpha_x=\frac{1}{\sqrt{N}}\) (11)

onde usamos notação decimal. Como vimos atrás, este estado pode ser conseguido aplicando o operador de Hadamard ao \(N\)-qubit \(|00\cdots0\rangle\). Veja as fórmulas (8) e (9):

\(|Q_0\rangle=H|00\cdots0\rangle\)

Vamos supôr, para simplificar a discussão, que \(N=2^n\), para um único inteiro positivo \(n\), então \(x\) pode ser representado, em numeração binária, por \(n\) bits. E portanto cada na \(\left|x\right\rangle\) sobreposição (11), é um \(n\)-qubit.

Como já disemos, a palhinha que procuramos (a agulha) está rotulada pelo índice a \(a\in\boldsymbol{\Sigma}\), que desconhecemos mas que queremos descobrir.

3. Para isso vamos utilizar um operador que tem um nome misterioso – um Oráculo Quântico!

O que é um oráculo quântico?

É uma caixa negra, cujo funcionamento interno não vamos discutir neste curto artigo, que tem a capacidade de reconhecer soluções para o problema de busca (da agulha no palheiro). O Oráculo deve ser pensado como uma “caixa negra" – como uma subrotina que pode ser consultada repetidamente.

Este reconhecimento é sinalizado pelo uso de um operador (chamado oráculo) \(O_f\), definido pela sua ação na base computacional:

\(|x\rangle|q\rangle\xrightarrow{O_f}|x\rangle|q\oplus_2f(x)\rangle)\) (12)

onde \(x\) representa os rótulos das palhinhas, \(\oplus_{2}\) é a adição módulo 2, e o qubit \(\left|q\right\rangle\) (dito de controlo) é um único qubit que é invertido se \(f(x)=1\), e permanece inalterado caso contrário. Aqui \(f=f_a:\Sigma\longrightarrow\{0,1\}\) é a função Booleana (a Indicatriz de \(a\)), definida por:

\(\left.f_a(x)=\left\{ \begin{aligned} & 1\quad\mathrm{se}\quad x=a \\ & 0\quad\mathrm{se}\quad x\neq a \end{aligned}\right.\right.\) (13)

Para verificar se \(x\) é a solução para o nosso problema de busca, preparamos o multi-quibit \(|x\rangle|0\rangle\), aplicamos o oráculo \(O_f\), e verificamos se o qubit de controlo foi invertido para \(\left|1\right\rangle\).

4. Observações: O oráculo \(O_f\), utilizado no algoritmo de Grover, é algo intrigante! De facto, parece que a utilização do oráculo induz um raciocínio circular no algoritmo. É preciso saber a para construir \(f_{a}(x)\) e depois usar \(f_{a}(x)\) para encontrar a! Então como é que sabemos antecipadamente o que é \(\left|a\right\rangle\), se é exatamente esse estado-alvo que queremos encontrar? Um bocado louco!...

De facto, essa é a pergunta certa! A resposta é que só precisamos de saber que alguém marcou o estado-alvo tornando a sua amplitude negativa. Não precisamos de saber o estado específico que foi marcado. A beleza do algoritmo é que “encontra” este estado automaticamente!

O oráculo faz exatamente essa marcação – é um espécie de Caixa Preta, pré-programada para verificar cada possível estado de entrada, e determinar qual, de entre todos esses estados possíveis, é o estado-alvo. Ele é configurado para reconhecer internamente o estado alvo. Algo como uma pergunta de sim/não para cada estado: “É este o alvo?”

A base para a confusão decorre de um mal-entendido sobre o significado e o propósito do oráculo. Para os informáticos, um oráculo é meramente um dispositivo matemático fictício que lhes permite estimar o custo computacional de algum algoritmo medido em unidades do “número de consultas ao oráculo”. No nosso exemplo, isto permite-lhes comparar os custos relativos da pesquisa não estruturada clássica com a pesquisa não estruturada quântica em termos de quantas vezes cada algoritmo deve consultar o oráculo.

Por outro lado, os físicos, sobretudo os experimentais, que de facto precisam de construir hardware de computação quântica, queixam- se porque alguém no seu laboratório precisa de escolher a para construir \(f_{a}(x)\), e depois um circuito quântico que desempenhe o papel do oráculo, \(O_f\).

No entanto, isto é semelhante à situação em que queremos encontrar o nome de alguém, conhecendo o seu número de telefone, usando uma lista telefónica.

Quem fez a lista telefónica, tem que saber qual o número de telefone associado a cada nome, e vice-versa. Portanto, a questão não é se a solução para o problema de busca é ou não conhecida antecipadamente, mas sim quantas vezes devemos consultar a lista antes de conhecermos a solução. No problema abstracto de pesquisa não estruturada, que é a situação do nosso exemplo das palhinhas, a lista é o oráculo, ou a função caixa-negra \(f=f_{a}(x)\).

No exemplo da lista telefónica, podemos resolver o problema da busca não estruturada num computador clássico, através de um procedimento conhecido como “gerar e testar”. Em que consiste? Imaginemos que temos um saco de rótulos e que, repetidamente, retiramos um rótulo e perguntamos ao oráculo se este é ou não o rótulo a da “agulha”. Se for, paramos. Caso contrário, repetimos o processo.

Este procedimento clássico pode ser expresso usando a mecânica quântica da seguinte forma: um análogo quântico do conjunto de rótulos pode ser considerado como a sobreposição, igualmente ponderada, de todos os rótulos no intervalo \(0\leq x\leq N-1\), ou seja, o estado \(\left|Q_{0}\right\rangle\) dado por (11). De forma semelhante, o análogo quântico do ato de retirar, aleatoriamente, um rótulo do saco de rótulos, pode ser considerado como o ato de escolher, nessa sobreposição, um . Depois, perguntamos ao oráculo “Será este a solução?”

5. O algoritmo de Grover começa com \(\left|Q_{0}\right\rangle\), a sobreposição uniforme de todos os estados.

Já sabemos o que fazer: preparamos o multi-quibit \(|x\rangle|0\rangle\), aplicamos o oráculo \(O_f\), e verificamos se o qubit de controlo foi invertido para \(\left|1\right\rangle\). Se foi, essa é a solução.

A questão agora é: quantas consultas deste tipo temos que fazer ao oráculo?

Clasicamente, como vimos, na pior das hipóteses temos que fazer, em média, \(N/2\) consultas. Quânticamente, Grover mostrou que esse número pode ser reduzido para \( \sqrt{N}\), em média.

O que fazer agora?

Para prosseguir, vamos seguir um exemplo concreto com \(N=8=2^3\) palhinhas.

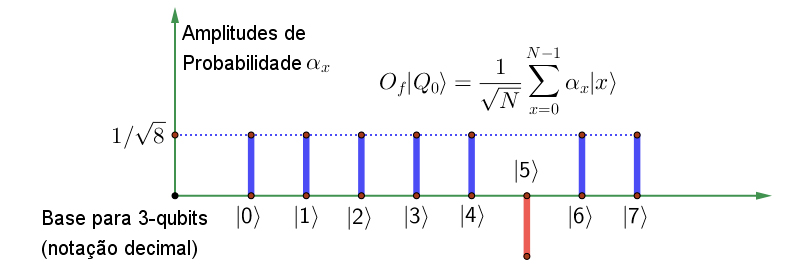
Como vimos, o Oráculo \(O_f\) marca o elemento procurado, alterando o sinal da sua amplitude de probabilidade. Se \(f(x)=0\), não acontece nada. Se \(f(x)=1\), o sinal da amplitude de probabilidade altera-se.

Como antes, prepararamos um 3-qubit \(\left|Q_{0}\right\rangle\) como uma única “sobreposição quântica” com amplitudes todas iguais a \(1/\sqrt{8}\) (ver a FIGURA 2). Em notação decimal:

\(|Q_0\rangle=\frac{1}{\sqrt{8}}\{|0\rangle+|1\rangle+|2\rangle+|3\rangle+|4\rangle+|5\rangle+|6\rangle+|7\rangle\}\) (14)

Suponhamos que a solução para o problema de pesquisa é a palhinha cujo rótulo \(a=5\) (este é apenas um exemplo ilustrativo. Na realidade, como já vimos, não sabemos qual é o verdadeiro estado-alvo!).

Aplicando o Oráculo \(O_f\) a \(\left|Q_{0}\right\rangle\), obtemos

Neste caso, o oráculo marca essa posição (que é o estado \(|101\rangle=|5\rangle\)) alterando a sua fase, isto é, multiplica a sua amplitude, que era igual a \(1/\sqrt{8}\), por \(-1\). A nova amplitude passa a ser \(-1/\sqrt{8}\).

Recorde que um número complexo pode ser escrito na forma polar: \(z=|z|e^{i\theta}\), onde \(\theta\in[0,2\pi[\) é a chamada fase de \(z\in\mathbb{C}\). Se multiplicarmos \(z\) por \(-1=e^{i\pi}\), obtemos \(-z=|z|e^{i\theta}e^{i\pi}\). A fase muda pois de \(\theta\) para \(\theta+\pi\) (módulo \(2\pi\)).Isto é, a amplitude do estado- -alvo foi multiplicada por \(-1\).

A chave para a pesquisa quântica é que podemos analisar todas as soluções simultaneamente (paralelismo quântico). O Oráculo manipula as amplitudes de probabilidade.

No entanto, isto não é não é suficiente! Porquê?

Porque alterar o sinal da amplitude de probabilidade não altera a probabilidade do elemento-alvo, pois a probabilidade é o quadrado do módulo da amplitude de probabilidade.

O próximo passo deve ser aumentar a amplitude do elemento-alvo enquanto diminui a amplitude dos outros, de modo a que uma medição forneça a solução com elevada probabilidade.

Inversão em torno da média.

O passo seguinte do algoritmo de Grover é a chamada de inversão em torno da média, que inverte todas as amplitudes de probabilidade, em relação à sua média \(\hat{\alpha}\). Esta é também conhecida como amplificação de amplitude.

A reflexão \(\R_{\hat{\alpha}}\), em torno da média \(\hat{\alpha}\), é representada matemáticamente pelo operador:

\(R_{\hat{\alpha}}:\alpha_i\longmapsto\alpha_i^{\prime}=2\hat{\alpha}-\alpha_i\) (15)

É aplicada após o Oráculo.

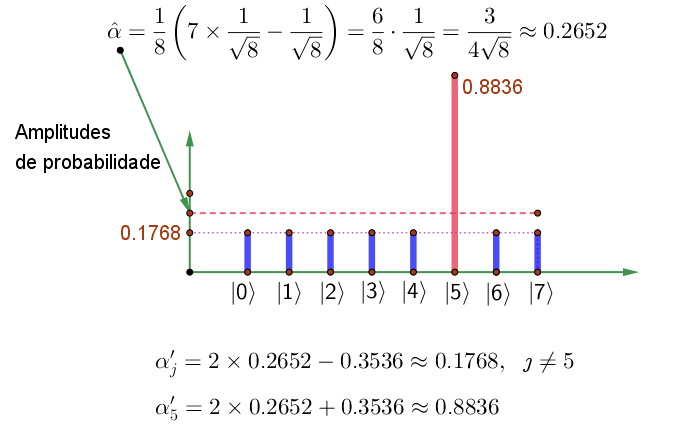
No exemplo

\(\hat{\alpha}=\frac{1}{8}\left(7\times\frac{1}{\sqrt{8}}-\frac{1}{\sqrt{8}}\right)=\frac{6}{8}\cdot\frac{1}{\sqrt{8}}=\frac{3}{4\sqrt{8}}\approx0.2652\)

A operação \(\R_{\hat{\alpha}}\), definida por (15), espelha todas as amplitudes em torno da sua média \(\hat{\alpha}\). Ou seja, ela faz com que as 7 amplitudes iguais fiquem menores e a amplitude “marcada”, fique ainda maior. Veja a FIGURA 3.

Podemos finalmente resumir todos estes passos no chamado:

Algoritmo de Grover:

Dados: Um conjunto não estruturado de \(N\) items (palhinhas) indistinguíveis, uma das quais é diferente das restantes (a “agulha”).

Objetivo: encontrar a “agulha”.

1. Inicialize o sistema com uma sobreposição quântica uniforme de todos os estados:

\(|Q_0\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle\)

2. Itere \(r(N)\) vezes o seguinte “iterador de Grover”

a) aplique o oráculo \(O_f\), definido por (12).

b) aplique a reflexão \(R_{\hat{\alpha}}\), definida por (15)

3. Meça o estado quântico resultante, na base computacional.

Par uma escolha correcta de \(r(N)\), o resultado será \(\left|a\right\rangle\), com probabilidade que converge para 1 quando \(N>>1\). É possível mostrar que \(r(N)\leq\left\lceil\frac{\pi}{4}\sqrt{N}\right\rceil\).

Uma interpretação geométrica.

O algoritmo de Grover admite uma interpretação geométrica, que tira partido do facto de que o estado quântico do algoritmo de Grover permanece sempre num subespaço bidimensional (um plano) após cada passo.

Consideremos o plano Π, gerado por \(\left|a\right\rangle\) e o \(\left|\right\rangle\)

\(|Q^{\prime}\rangle=\frac{1}{\sqrt{N}}(|Q_0\rangle-|a\rangle)=\frac{1}{\sqrt{N-1}}\sum_{x\neq a}|x\rangle\in|a\rangle^\perp\)

que está no hiperplano \(|a\rangle^{\perp}\), perpendicular a \(\left|a\right\rangle\).

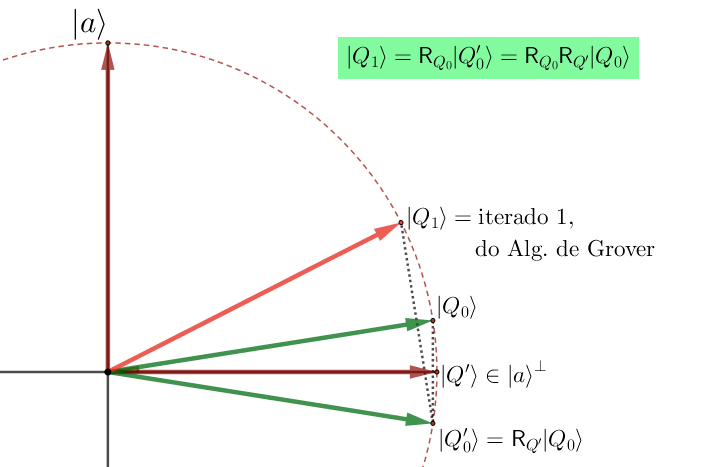
O algoritmo de Grover começa com o \(\left|\right\rangle\) inicial \(\left|Q_{0}\right\rangle\), dado por (11), que pertence ao plano Π referido. Consideremos a reflexão \(R\), relativamente ao hiperplano \(|a\rangle^{\perp}\), que atua como um espelho para vetores no plano Π. Isto é, nesse plano atua como uma reflexão \(R_{Q^{\prime}}\), relativamente à reta gerada por \(\left|Q^{\prime}\right\rangle\).

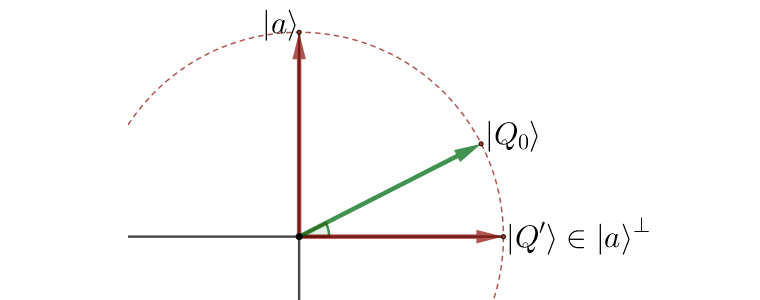
Seja

\(|Q_0^{\prime}\rangle=R_{Q^{\prime}}|Q_0\rangle\)

Consideremos ainda a reflexão \(R_{Q_0}\), relativamente à reta gerada por \(\left|Q_{0}\right\rangle\), e seja

\(|Q_1\rangle=R_{Q_0}|Q_0^{\prime}\rangle=R_{Q_0}R_{Q^{\prime}}|Q_0\rangle\)

Na FIGURA 5, o ângulo entre \(\left|Q_{0}\right\rangle\) e \(\left|Q'\right\rangle\) é apenas ligeiramente maior que 0. O algoritmo amplia iterativamente esta pequena diferença, para que \(\left|Q_{1}\right\rangle\), \(\left|Q_{2}\right\rangle\), · · · se aproximem cada vez mais do estado-alvo \(\left|a\right\rangle\). Tudo o que precisamos de fazer é rodar \(\left|Q_{0}\right\rangle\) em direção a \(\left|a\right\rangle\), passando por estados intermédios \(\left|Q_{1}\right\rangle\), \(\left|Q_{2}\right\rangle\), · · · .

O “truque” é construir a rotação como um produto de reflexões. A primeira reflexão atua sobre o estado de sobreposição inicial \(\left|Q_{0}\right\rangle\) e reflete-o em relação à reta gerada por \(\left|Q'\right\rangle\). Isto tem o efeito de multiplicar por −1 a amplitude associada a \(\left|a\right\rangle\), que faz parte da sobreposição \(\left|Q_{0}\right\rangle\).

A segunda etapa reflete o novo estado \(|Q_0^{\prime}\rangle\) em relação à reta gerada pelo estado inicial \(\left|Q_{0}\right\rangle\) para produzir o estado \(\left|Q_{1}\right\rangle\) que agora está mais próximo do alvo \(\left|a\right\rangle\).

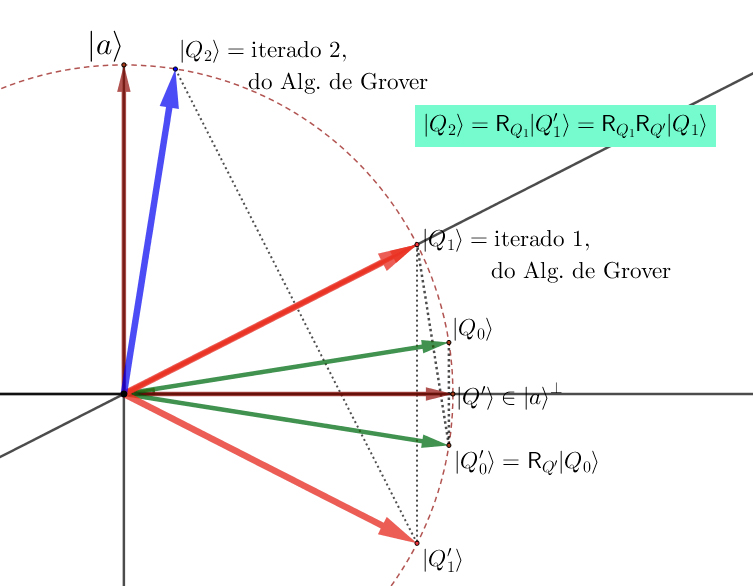
Essa etapa configura então todas as etapas subsequentes. Veja a FIGURA 5. Na FIGURA 6 vemos a 2ª iteração do algoritmo, obtida substituindo \(\left|Q_{0}\right\rangle\) por \(\left|Q_{1}\right\rangle\) e fazendo as duas reflexões indicadas.

E para já é tudo! Fica o aperitivo que espero tenha aberto o apetite para um estudo mais profundo.

Voltaremos ao assunto numa revista posterior.