Parábola da Fábrica Quântica.

Começamos com uma curta parábola sobre uma fábrica quântica da qual podemos encomendar quatro tipos de objetos, distinguidos por duas propriedades:

COR: azul ou vermelha \((\color{blue}{A},\color{red}{V}\color{black})\)

FORMA: triângulos ou quadrados \((T,Q\))

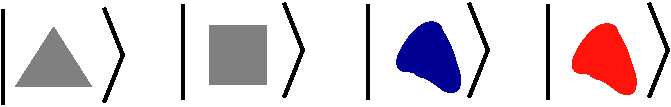
A nossa primeira encomenda é de 100 objetos de COR azul. Recebida a encomenda, quisemos verificar se estava em ordem. Para isso dispomos de um medidor de COR, ilustrado na FIGURA 2.

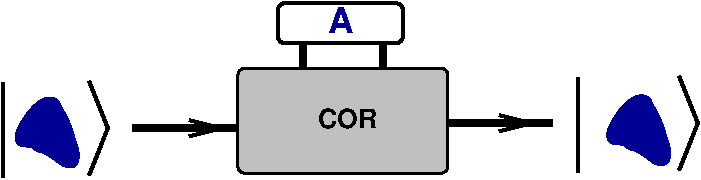
Passando os objetos do lote pelo aparelho, podemos verificar que o mostrador indica sempre \(\color{blue}{A}\). O processo pode ser usado para todos os quatro tipos de objetos porque, além do medidor de COR, temos também um medidor de FORMA. Se uma propriedade é física, pode ser medida.

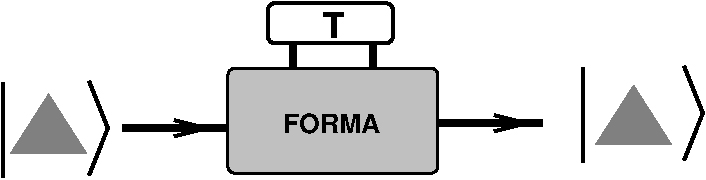
A curiosidade leva-nos agora a investigar a FORMA dos objetos da nossa primeira encomenda. Para isso, usamos o medidor de FORMA no lote de 100 \(\color{blue}{A}\); o resultado é que perto de metade são \(T\) e a outra metade \(Q\). Estes resultados ocorrem de maneira aleatória e sem qualquer ordem percetível. Exatamente o mesmo se passa com encomendas de objetos de tipo \(\color{red}{V}\). A COR é previsivelmente vermelha, mas em medições de FORMA obtemos o mesmo resultado que para objetos de COR \(\color{blue}{A}\).

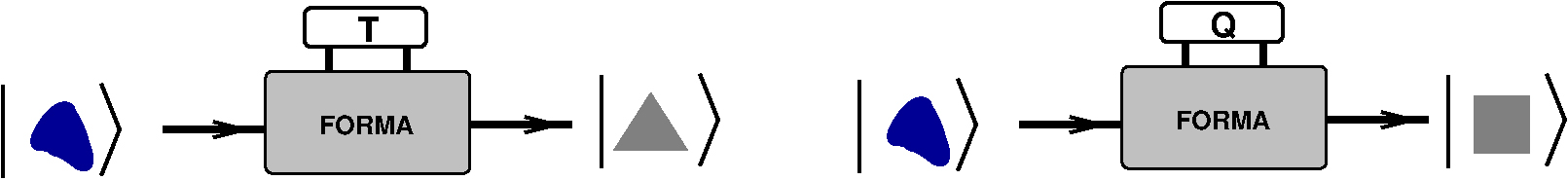
Algo semelhante se passa com as encomendas de objeto de FORMA \(T\) (ou \(Q\)): em medições de COR obtemos perto de metade de objetos de cada cor possível.

Nesta altura interrogamos-nos: será que poderemos encomendar objetos com FORMA e COR definidas, representados por \(\left |\color{red}{\blacktriangle}\right >\), \(\left |\color{red}{\blacksquare}\right >\), \(\left |\color{blue}{\blacktriangle}\right >\), ou \(\left |\color{blue}{\blacksquare}\right >\)? Resolvemos encomendar um lote de \((T,\color{red}{V})\), (TRIÂNGULOS, VERMELHOS). A resposta da fábrica é surpreendente: não só não podem fornecer tal lote, como defendem que ninguém pode, porque tais objetos não existem.

Vemos imediatamente uma oportunidade de inovação. Porque não encomendar um lote de COR \(\color{red}{V}\) e usar um medidor de FORMA, para selecionar desse lote apenas os \(T\)? Dito e feito, assim procedemos e selecionamos cerca de metade dos objetos do lote \(\color{red}{V}\), aqueles cuja FORMA foi medida como \(T\). Mas será assim tão fácil? Os nossos medidores vendem-se em qualquer loja. Porque é que a fábrica se recusou a cumprir a encomenda?

Esta dúvida leva-nos a investigar a COR dos objetos selecionados e a compreender a dificuldade da fábrica. De um modo imprevisível, cerca de metade dos objetos selecionados com a FORMA \(T\) permanecem \(\color{red}{V}\), mas outros tantos são agora \(\color{blue}{A}\). Continuando a investigação, procurando outros processos de medir FORMA e COR, encomendando da concorrência, etc., somos levados à mesma conclusão que a fábrica: não existem objetos em que tenhamos, em simultâneo, a definição das duas variáveis físicas, FORMA e COR.

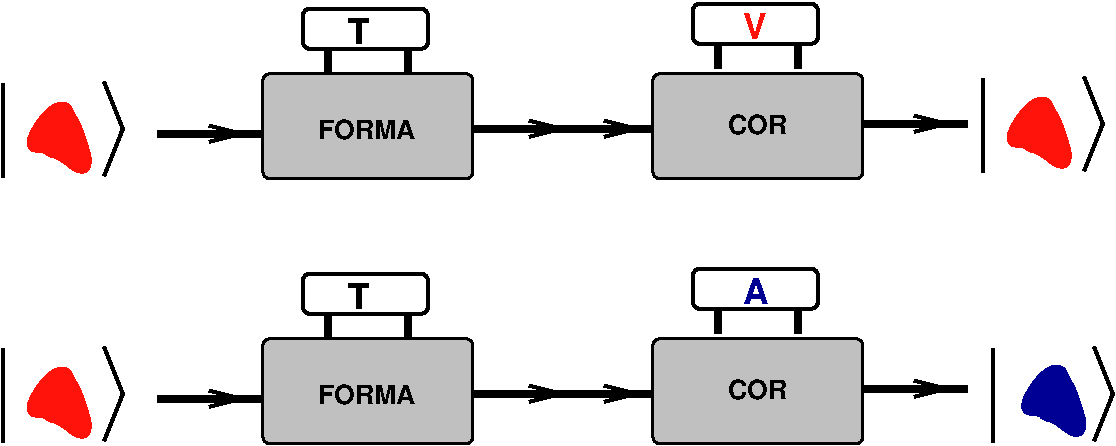
Variáveis incompatíveis.

Esta pequena parábola ilustra um comportamento da Natureza que está no cerne da distinção entre a Mecânica Quântica e a Física Clássica (Relatividade Geral e Restrita, incluídas). A FORMA e a COR são duas grandezas físicas, que, neste exemplo, só têm dois valores possíveis. Poder-se-ia pensar que, só por aí, dada a natureza discreta desta variáveis, já estamos no domínio quântico. Mas não é a distinção entre grandezas discretas e contínuas que nos importa aqui. Existem modelos puramente clássicos em que podemos definir variáveis discretas. O que se verifica neste exemplo da FORMA e COR é que estas variáveis são incompatíveis. Qualquer tentativa de preparar um sistema de modo a ter valores definidos de duas variáveis incompatíveis, como COR e FORMA, está votado ao fracasso, pura e simplesmente porque tais sistemas não existem na natureza. A existência de variáveis físicas incompatíveis é a essência da Física Quântica. Na Física Clássica não há grandezas físicas incompatíveis. Se os nossos objetos fossem clássicos não teríamos dificuldade em encontrá-los num dos quatro estados de COR e FORMA definidas, \(\{|\color{blue}{A}\color{black},T\rangle,|\color{blue}{A}\color{black},Q\rangle,|\color{red}{V}\color{black},T\rangle,|\color{red}{V}\color{black},Q\rangle\}\). Sendo estas variáveis incompatíveis só temos ou estados de COR definida \(\{|\color{blue}A\color{black}\rangle,|\color{red}{V}\color{black}\rangle\}\) ou de FORMA definida, \(\{|T\rangle,|Q\rangle\}\).

Para ver, com um mínimo de rigor, como é que a Mecânica Quântica trata esta situação teremos de introduzir uma característica extra dos objetos quânticos da parábola. Nada do que dissemos até agora exclui a possibilidade de uma terceira propriedade dos objetos, compatível com uma das anteriores. Podia acontecer que a TEXTURA, uma grandeza com dois valores, \(R\) (rugoso) e \(M\) e (macio), ao contrário da FORMA, fosse compatível com COR. A fábrica poderia fornecer dois lotes distintos de objetos \({\color{Blue} A}\): um lote com textura \(R\) e outro com textura \(M\). Seriam distinguíveis por medição de TEXTURA , mas numa medição de COR dariam o resultado \({\color{Blue} A}\) com probabilidade 1. Esta é certamente a situação mais geral, pois o valor de uma única grandeza raramente chega para caracterizar o estado de um objeto físico. Porém, para simplificar, vamos supor que não existe nenhuma variável compatível com COR (ou com FORMA), ou seja, não é possível refinar a caracterização física de um objeto para além de especificar a COR ou a FORMA. Este exemplo simples é suficiente para explicar o princípio da sobreposição, o modo como se lida nas teorias quânticas com a incompatibilidade de grandezas. A propósito, a situação destas variáveis de ficção, FORMA e COR, é exatamente a que verifica entre duas componentes do spin de um eletrão ou de dois estados de polarização de um fotão. Não é incomum encontrar teorias quânticas exatamente com esta forma.

Seja como for, com esta simplificação, não é possível distinguir dois objetos de um lote de COR definida. Seguramente não pela medição de FORMA, pois se o fizermos deixamos de ter objetos de COR definida. Dizemos que um objeto de lote azul está num estado quântico \(\left|\color{blue}A\right\rangle\) e do lote vermelho no estado \(\left|\color{red}V\right\rangle\). Indicar um destes dois estados é dar uma descrição completa do objeto, que não é passível de especificação adicional. Do mesmo modo, há dois estados \(\left|T\right\rangle\) e \(\left|Q\right\rangle\) para objetos de lotes de FORMA definida, cada um dos quais estabelece a caracterização mais completa possível do estado do objeto.

Resta saber qual é a relação entre estes dois pares de estados, associados a variáveis incompatíveis.

Princípio de Sobreposição.

A fábrica fornece-nos um objeto num destes 4 estados \(\{|\color{blue} A\color{black}\rangle,|\color{red}V\color{black}\rangle,|T\rangle,|Q\rangle\}\) sem dizer qual. Podemos escolher entre medir a COR ou a FORMA. Se optarmos pela segunda e obtivermos \(T\), concluímos que o estado não era \(|Q\rangle\), — \(|Q\rangle\) e \(|T\rangle\) são realmente distintos —, mas não conseguimos determinar se o estado era \(|T\rangle\), \(|\color{blue} A\color{black}\rangle\) ou \(|\color{blue} A\color{black}\rangle\); o objeto podia estar no estado \(|T\rangle\), ou ter COR definida, \(|\color{blue} A\color{black}\rangle\) ou \(|\color{blue} A\color{black}\rangle\), uma vez que estes dois estados podem dar o mesmo resultado que \(|T\rangle\) numa medição de FORMA, com probabilidade de 50%. O estado \(|\color{blue} A\color{black}\rangle\) é em parte o estado \(|T\rangle\) e em parte o estado \(|Q\rangle\). Na linguagem da mecânica quântica, o estado \(|\color{blue} A\color{black}\rangle\) é uma sobreposição quântica dos estados \(|T\rangle\) e \(|Q\rangle\). O mesmo podemos dizer do estado \(|\color{blue} A\color{black}\rangle\) uma vez, que numa medição de FORMA ele pode, tal como \(|\color{blue} A\color{black}\rangle\), dar o mesmo resultado que \(|T\rangle\), ou que \(|Q\rangle\).

O mesmo se passa se escolhermos medir COR: o resultado será sempre \(\color{blue} A\) ou \(\color{red} V\), mesmo que o estado inicial seja \(|T\rangle\) ou \(|Q\rangle\). Por outras palavras, os estados \(|T\rangle\) e \(|Q\rangle\) são sobreposições quânticas de \(|T\rangle\)\) e \(|\color{red}V\color{black}\rangle\).

É muito possível que o leitor já tenha ouvido falar da computação quântica e tenha lido a explicação que, enquanto num computador clássico um bit — sistema com dois estados apenas como no nosso exemplo — só pode ter os valores 0 ou 1, num computador quântico pode estar num sobreposição arbitrária destes dois valores. O que esta explicação deixa de fora, e que o nosso exemplo ilustra, é que todos os estados quânticos, incluindo 0 e 1, são sobreposição de outros estados.

A Teoria Quântica de FORMA e COR.

Para completar o tratamento quântico desta situação, vamos ter de usar um pouco mais de matemática do que nas secções anteriores.

A Mecânica Quântica trata os estados como vetores. O leitor está familiarizado com vetores no espaço, representados por segmentos orientados com direção, sentido e módulo. As operações fundamentais sobre vetores são a soma, \(\vec{c}=\vec{a}+\vec{b}\), multiplicação por um número real (por um escalar), \(\vec{c}=\lambda\vec{a}\), e o produto interno (ou produto escalar), \(\vec{a}\cdot\vec{b}=ab\cos\left(\theta\right)\). O conceito de vetor, em matemática, generaliza-se a quaisquer conjuntos nos quais possam ser definidas estas operações^b. Se os estados são vetores, podem multiplicar-se por escalares — que em mecânica quântica são números complexos — e podem somar-se para definir novos estados. Essa é a expressão matemática do princípio de sobreposição.

Da discussão anterior resulta que qualquer estado se pode escrever como sobreposição de \(\left|\color{blue}A\right\rangle\) e \(\left|\color{red}V\right\rangle\), porque, na medição de COR, dá o mesmo resultado que um dos estados \(\left|\color{blue}A\right\rangle\) ou \(\left|\color{red}V\right\rangle\):

\(\left|\Psi\right\rangle=a\left|\color{blue}A\right\rangle+b\left|\color{red}V\right\rangle\) (1)

O mesmo se aplica a \(|T\rangle\) e \(|Q\rangle\)

\(\left|\Psi\right\rangle=c\left|T\right\rangle+d\left|Q\right\rangle\) (2)

Os escalares \((a,b)\) e \((c,d)\) são designados como amplitudes de probabilidade e têm o seguinte significado: \(\left | a\right |^2\), é a probabilidade de o estado \(\left|\Psi\right\rangle\) ser o estado \(\left|\color{blue}A\right\rangle\) numa medição de COR, \(\left | b\right |^2\) a probabilidade de ser \(\left|\color{red}V\right\rangle\) e assim sucessivamente.

As nossas observações sobre FORMA e COR podem ser traduzidas por

\(|T\rangle{=}\frac{1}{\sqrt{2}}|\color{blue}A\color{black}\rangle{+}\frac{1}{\sqrt{2}}|\color{red}V\color{black}\rangle\) (3)

e

\(|Q\rangle{=}\frac{1}{\sqrt{2}}|\color{blue}A\color{black}\rangle{-}\frac{1}{\sqrt{2}}|\color{red}V\color{black}\rangle\) (4)

Somando e subtraindo estas suas equações facilmente as invertemos para obter

\(|\color{blue}A\color{black}\rangle{=}\frac{1}{\sqrt{2}}|T\color{black}\rangle{+}\frac{1}{\sqrt{2}}|Q\rangle\) (5)

\(|\color{red}V\color{black}\rangle{=}\frac{1}{\sqrt{2}}|T\color{black}\rangle{-}\frac{1}{\sqrt{2}}|Q\rangle\), (6)

o que dá conta dos resultados de medições de FORMA em estados de cor definida. Tal como afirmado no final da secção anterior, qualquer dos 4 estados da parábola é sobreposição de dois estados distintos.

Notas finais.

1. Da mesma maneira que a fábrica produz lotes de um dado estado, pode criar um lote em que metade dos objetos sejam \(|\color{blue}A\color{black}\rangle\) e metade sejam \(|\color{red}V\color{black}\rangle\), em sequência aleatória. Em que medida é que o estado da equação (3) se distingue dessa possibilidade? Numa medição de COR os resultados com tal lote ou com um lote no estado da estado da equação (3) seriam idênticos. Porém essas duas situações dão resultados muito diferentes numa medição de FORMA. Um objeto de um lote no estado \(|\color{blue}A\color{black}\rangle\) ou no estado \(|\color{red}V\color{black}\rangle\) tem igual probabilidade de ter FORMA \(T\) ou \(Q\). Por isso um lote com uma mistura de \(|\color{blue}A\color{black}\rangle\) e \(|\color{red}V\color{black}\rangle\) mostra ter metade das vezes FORMA \(T\) e metade \(Q\); mas o estado da equação (3) tem sempre FORMA \(T\) e nunca \(Q\). A sobreposição de estados é um estado, para o qual existe uma ou mais medições cujo resultado é perfeitamente definido. Um mistura de estados, como a que foi descrita acima, inclui além da incerteza inerente à natureza quântica das variáveis incompatíveis, uma incerteza clássica, relacionada com o desconhecimento do estado em que objeto se encontra.

2. Dizemos que as amplitudes de cada componente do estado da equação (3) — \((1/\sqrt{2},1/\sqrt{2})\) —, na medição de FORMA, interferem construtivamente para o resultado \(T\) e destrutivamente para o resultado \(Q\). Para amplitudes \((1/\sqrt{2},-1/\sqrt{2})\) da equação (4) verifica- se o oposto. O sinal relativo das amplitudes da sobreposição^c é fisicamente relevante, não apenas o respetivo quadrado do módulo, a probabilidade.

3. Uma palavra sobre a função de onda de Schrödinger, \(\psi\left(\vec{r}\right)\). Tem exatamente a mesma natureza que as amplitudes \(a\) e \(b\) da equação (1). Só que em vez de uma sobreposição de dois estados de COR definida, refere-se a um contínuo de estados de POSIÇÃO definida, \(\{\left|\vec{r}\right\rangle,\vec{r}\in R^3\}\). Daí vem a interpretação e Born de \(|\psi(\vec{r})|^2\) como densidade de probabilidade de posição. Tal como no exemplo da parábola, isso não esgota o significado da função de onda. Por exemplo, só certas funções de onda correspondem a estados em que a grandeza física ENERGIA — incompatível com POSIÇÃO — tem um valor definido. A equação de Schrödinger serve precisamente para encontrar esses estados.

4. A discussão sobre os objetos provenientes da fábrica quântica baseou-se na afirmação de que não existem objetos com COR e FORMA definidas em simultâneo. A especificação de COR (ou de FORMA) é uma especificação tão completa como possível e por essa razão a FORMA de um objeto de COR definida é imprevisível. Mas será isto verdade? Podíamos conceber que dois objetos de COR definida poderiam ser distinguidos por uma outra variável (por exemplo, \(S=\pm1\)), cujo valor determinaria a FORMA, mas que, por alguma razão, fosse inacessível à experiência: a fábrica não consegue produzir objetos de COR definida sempre com o mesmo valor de , e não existem medidores \(S\) de que permitam escolher dos objetos de uma dada COR os que tem um dado valor de \(S\) — se existissem, a fábrica poderia usá-los para criar objetos de COR e \(S\) definidos. \(S\) é uma variável escondida. A discussão sobre esta questão merece um outro artigo. Aqui apontaremos apenas que a descrição quântica não tem variáveis escondidas. Em vez disso reconhece a possibilidade de as grandezas físicas manifestas serem incompatíveis. Além disso, John Bell, em 1964, provou que certas experiências particulares, feitas com pares de objetos quânticos arbitrariamente distantes, permitem distinguir as previsões da Mecânica Quântica de qualquer teoria que assuma que os resultados de medições sobre cada um dos objetos do par seja determinado, ainda que desconhecido, pelas tais variáveis escondidas. As experiências até hoje realizadas confirmaram sempre, de modo inequívoco, as previsões da Mecânica Quântica. Mas isso é assunto para outra história.

Notas

^a Verhoeven, P., Hollow Man. 2000.

^b Em rigor, o produto interno não é necessário para definir vetores; mas é o que permite a introdução das noções de ângulos e distâncias para vetores abstratos.

^c Ou fase relativa no caso de amplitudes complexas.