Na ausência de experiências concretas para testar os aspectos de realidade e localidade da mecânica quântica, o debate sobre os fundamentos da mecânica quântica manteve-se durante muito tempo no âmbito da Filosofia. Também nada se concluiu sobre se a inclusão de “variáveis ocultas” (ou auxiliares) na descrição da mecânica poderia torná-la completa, isto é, numa teoria determinística como, por exemplo, a mecânica quântica Newtoniana.

A situação mudou drasticamente em 1964, quando John Bell propôs uma desigualdade que teria que ser satisfeita por qualquer teoria que tivesse os dois atributos — localidade e realidade.

Essa desigualdade envolve quantidades experimentalmente mensuráveis e, portanto, oferece a possibilidade de testar experimentalmente se a mecânica quântica satisfaz essa desigualdade. Se a viola, então concluímos que a mecânica quântica não satisfaz, ou o atributo da localidade, ou o da realidade.

localidade realidade \(\Rightarrow \) desigualdade de Bell

violação da desigualdade de Bell \(\Rightarrow \) não localidade ou não realidade (1)

A Desigualdade de Bell (na forma Clauser-Horne-Shimony-Holt (CHSH)) demonstra matematicamente a incompatibilidade entre o realismo local e as previsões da mecânica quântica. Inspirada na simplicidade da chamada “Máquina de Mermin”, que vamos descrever, a dedução clássica assume que as partículas possuem propriedades predefinidas (realismo) que não são influenciadas instantaneamente por medições distantes (localidade).

Essa dedução estabelece um limite para as correlações que podem ser observadas num universo regido pelo realismo local. A mecânica quântica, por outro lado, ao descrever o comportamento de partículas entrelaçadas, prevê correlações que violam este limite, uma previsão consistentemente confirmada por inúmeras experiências. Esta violação tem implicações profundas, indicando que a natureza é inerentemente não-local ou não-realista, forçando-nos a questionar a nossa intuição clássica sobre a natureza da realidade, a localidade e a objetividade das propriedades físicas.

1. A Crise da Intuição Clássica.

Desde o seu nascimento, a mecânica quântica desafiou as nossas concepções mais fundamentais sobre a realidade. Albert Einstein, uma das mentes mais brilhantes do século XX, sentia-se profundamente desconfortável com a ideia de que a natureza poderia ser fundamentalmente probabilística e com o que ele chamava de “ação fantasmagórica à distância” (em inglês, spooky action at a distance). Esta expressão referia-se ao fenómeno do entrelaçamento (entanglement), onde duas partículas parecem estar intrinsecamente ligadas, independentemente da distância que as separa.

No famoso artigo EPR de 1935 (Einstein-Podolsky-Rosen), Einstein e seus colaboradores argumentaram que a mecânica quântica era uma teoria incompleta. Eles propuseram que deveria haver “variáveis ocultas” — informações adicionais e mais profundas sobre as partículas, que a mecânica quântica não descrevia — e que, se conhecidas, eliminariam a necessidade de qualquer “fantasmagoria”. Essencialmente, eles defendiam a ideia de realismo local:

• Realismo: As partículas possuem propriedades bem definidas antes de serem medidas. A medição apenas revela essas propriedades, não as cria.
• Localidade: Nenhuma influência física pode viajar mais rápido que a velocidade da luz. A medição de uma partícula não pode influenciar instantaneamente o estado de outra partícula distante.

Se o realismo local fosse verdadeiro, o universo funcionaria de uma maneira mais intuitiva, onde tudo tem uma causa local e propriedades predefinidas.

O Desafio de John Bell.

Foi John Bell, em 1964, quem transformou esta disputa filosófica numa questão experimentalmente testável. Bell demonstrou que se o realismo local fosse verdadeiro, as correlações observadas em certas experiências (envolvendo pares de partículas entrelaçadas) deveriam obedecer a um limite matemático — as desigualdades de Bell. Se a mecânica quântica estivesse correta, e o entrelaçamento fosse uma característica fundamental da realidade, então essas desigualdades seriam violadas.

2. Introdução: O Paradoxo e a Máquina de Mermin.

A “Máquina de Mermin”é uma ferramenta conceptual poderosa, criada por N. David Mermin, para tornar a prova da Desigualdade de Bell mais acessível e intuitiva, especialmente na sua versão CHSH (Clauser-Horne-Shimony-Holt).

O que Bell demonstrou é que, sob as premissas de realismo local (as propriedades das partículas são predefinidas independentemente da medição, e a medição de uma não afeta instantaneamente a outra), a correlação observada entre os resultados de Alice e Bob deve satisfazer certas desigualdades. A mecânica quântica, no entanto, prevê que para estados entrelaçados, essas desigualdades podem ser violadas.

Vamo-nos focar na Desigualdade de CHSH (Clauser-Horne-Shimony-Holt), uma das formas mais populares e testáveis da Desigualdade de Bell.

3. Configuração da Experiência (Máquina de Mermin).

Suponhamos Alice e Bob são dois cientistas situados em galáxias distantes, sem possibilidade de comunicação. Eles recebem pares de partículas, \(A\) e \(B\) (por exemplo, fotões ou eletrões), que foram criadas juntas numa fonte central e emitidas em direção a dois detetores, um operado por Alice e outro por Bob. (FIGURA 1).

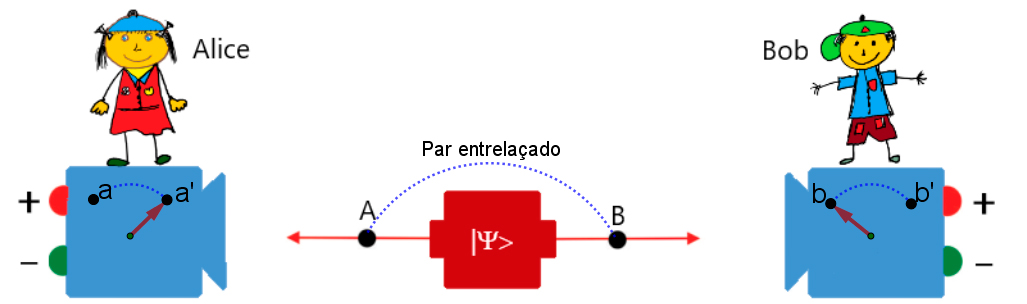
Alice tem um detetor com dois ponteiros que medem dois possíveis atributos binários: \(a\) e \({a}'\), cada um dos quais pode tomar apenas dois valores possíveis: ou , indicados pelo acender, respetivamente, de uma lâmpada vermelha (valor ) ou de outra verde (valor ). Bob tem um detetor com uma configuração completamente análoga à de Alice, mas com dois outros atributos binários \(b\) e \({b}'\\).

Alice e Bob realizam as suas medições de forma independente e não podem comunicar entre si durante o experiência. Eles apenas comparam os seus resultados, e medem as correlações entre os seus resultados após um grande número de ensaios.

4. Derivação Clássica (Assumindo Realismo Local).

Vamos agora usar o que Mermin nos ensinou: se as partículas são “clássicas” e obedecem ao realismo local, o que podemos esperar?

1. Realismo (Variáveis Ocultas): Cada partícula, ao ser emitida, já “sabe” os resultados dos seus atributos, mesmo antes de eles serem medidos pelos detetores. Por outras palavras, o resultado de qualquer medição é predeterminado por alguma variável oculta \(\lambda\), que representa as propriedades preexistentes de ambas as partículas, antes de qualquer medição.

• A partícula, \(A\) de Alice já possui um valor \(a_{A}\left ( \lambda \right )\in \left\{ -1,+1\right\}\), para a medição do atributo \(a\), e um valor \({a}_A'\left ( \lambda \right )\in \left\{ -1,+1\right\}\) para a medição de \(a'\).
• O mesmo acontece com a partícula de Bob — ela já possui um valor \(b_B\left ( \lambda \right )\in\left\{ -1,+1\right\}\) para a medição de \(b\), e um valor \(b_B'\left ( \lambda \right )\in\left\{ -1,+1\right\}\) para a medição \(b'\).

2. Localidade: O resultado da medição de um atributo da partícula de Alice depende apenas desse atributo e da variável , e o mesmo acontece para a partícula de Bob. Isto é, os resultados obtidos pelo detetor de Alice em nada influenciam os obtidos pelo detetor de Bob, e vice-versa. Não há comunicação instantânea ou “ação fantasmagórica”.

Consideremos agora a seguinte quantidade para cada ensaio individual:

\(S_{\mathrm{cl\acute{a}ssico}}(\lambda)=a_{A}(\lambda)b_{B}(\lambda)+a_{A}(\lambda)b_{B}^{\prime}(\lambda)+a_{A}^{\prime}(\lambda)b_{B}(\lambda)-a_{A}^{\prime}(\lambda)b_{B}^{\prime}(\lambda)\) (2)

Podemos reescrever esta expressão fatorizando os termos:

\(S_{\mathrm{cl\acute{a}ssico}}(\lambda)=a_{A}(\lambda)[b_{B}(\lambda)+b_{B}^{\prime}(\lambda)]+a_{A}^{\prime}(\lambda)[b_{B}(\lambda)-b_{B}^{\prime}(\lambda)]\)

Como \(b_B\left ( \lambda \right )\) e \(b_B'\left ( \lambda \right )\) só podem ser \(+\\) ou \(-\\), os termos entre parênteses têm valores limitados:

• Se \(b_B(\lambda)=b_{B}^{\prime}(\lambda)\), então \([b_B(\lambda)-b_B^{\prime}(\lambda)]=0\),e \([b_B(\lambda)+b_B^{\prime}(\lambda)]=\pm2\).
• Se \(b_B(\lambda)\neq b_{B}^{\prime}(\lambda)\), então \([b_B(\lambda)+b_B^{\prime}(\lambda)]=0\),e \([b_B(\lambda)-b_B^{\prime}(\lambda)]=\pm2\).

Em qualquer um dos casos, um dos parênteses é \(\pm 2\) e o outro é . Portanto, a expressão para \(S_{\mathrm{cl\acute{a}ssico}}\) torna-se:

\(S_{\mathrm{cl\acute{a}ssico}}{(\lambda)}=a_A(\lambda)(\pm2)\mathrm{~ou~}S_{\mathrm{cl\acute{a}ssico}}{(\lambda)}=a_A^{\prime}(\lambda)(\pm2)\)

Como \(a_{A}(\lambda)\) e \(a_{A}^{\prime}(\lambda)\) também são \(\pm\), o valor absoluto de \(S_{\mathrm{cl\acute{a}ssico}}\) para qualquer \(\lambda\) é:

\(|S_{\mathrm{cl\acute{a}ssico}}(\lambda)|=|(\pm1)(\pm2)|=2\)

Agora, consideremos o valor esperado (ou média) desta quantidade calculada com muitos ensaios. Se \(p(\lambda)\) é a distribuição de probabilidade da variável oculta \(\lambda\) (que desconhecemos), que, por simplicidade, supomos ser discreta:

\(\langle S_{\mathrm{cl\acute{a}ssico}}\rangle=\sum_{\lambda}S_{\mathrm{cl\acute{a}ssico}}(\lambda)p(\lambda)\)

Tomando o valor absoluto da média:

\(|\langle S_{\mathrm{cl\acute{a}ssico}}\rangle|=\left|\sum_{\lambda}S_{\mathrm{cl\acute{a}ssico}}(\lambda)p(\lambda)\right|\)

Sabemos que \(|S_{\mathrm{cl\acute{a}ssico}}(\lambda)|\leq2\) para cada \(\lambda\). Assim,

\(|\langle S_{\mathrm{cl\acute{a}ssico}}\rangle|\leq\sum_{\lambda}|S_{\mathrm{cl\acute{a}ssico}}(\lambda)|p(\lambda)\leq\sum_{\lambda}2p(\lambda)=2\sum_{\lambda}p(\lambda)=2\times1=2\)

Portanto, a Desigualdade de Bell (CHSH) para teorias de realismo local é:

\(|\langle S_{\mathrm{cl\acute{a}ssico}}\rangle|\leq2\) (3)

Esta é a Desigualdade de Bell (CHSH). Ela nos diz que, se o universo for governado por realismo local, as correlações medidas entre Alice e Bob nunca podem exceder o valor de \(2\).

Desigualdade de Bell (CHSH) Clássica:

\(|\langle S_{\mathrm{cl\acute{a}ssico}}\rangle|=|\langle a_Ab_B\rangle+\langle a_Ab_B^{\prime}\rangle+\langle a_A^{\prime}b_B\rangle-\langle a_A^{\prime}b_B^{\prime}\rangle|\leq2\)

Onde \(\langle x_{A}y_{A}\rangle\) é o valor esperado do produto dos resultados de Alice (para o atributo \(x\)) e Bob (para o atributo \(y\)).

5. Previsão da Mecânica Quântica.

Agora, vamos calcular o valor esperado da mesma quantidade usando a mecânica quântica, para um par de partículas entrelaçadas.

Suponhamos que as medições de Alice e Bob correspondem a operadores de spin \(x_{A}=x\cdot\sigma_{A}\) e \(y_{B}=y\cdot\sigma_{B}\), onde \(x_{A}=a,a^{\prime}\) e \(y_{B}=b,b^{\prime}\) são vetores unitários que representam as direções segundo as quais se mede o spin pelos detetores detetores, e \(\sigma=(\sigma_{x},\sigma_{y},\sigma_{z})\) são as matrizes de Pauli

\(\sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix};\sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix};\sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\) (4)

Os resultados das medições são \(\pm\) (spin UP e DOWN).

Consideremos agora um estado entrelaçado (singleto), como o estado de Bell:

\(|\Phi\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)\) (5)

Este é um estado maximamente entrelaçado, onde as propriedades de spin das duas partículas estão perfeitamente correlacionadas, mas indefinidas individualmente até à medição.

Os atributos que vão ser medidos pelo detetor de Alice \((a,a^{\prime})\), e pelo de Bob \((b,b^{\prime})\), correspondem a medir o spin das partículas em direções específicas no espaço, definidas por vetores unitários \((a,a^{\prime})\) para Alice e \((b,b^{\prime})\) para Bob.

Para a equação (5), o valor esperado do produto das medições é:

\(\langle x_{A}\otimes y_{B}\rangle=\langle\Phi|(x\cdot\sigma_{A})\otimes(y\cdot\sigma_{B})|\Phi\rangle=x\cdot y=\cos(\theta_{xy})\) (6)

onde \(\theta_{xy}\) é o ângulo entre as direções de medição.

Assim, o valor esperado da quantidade \(S\) na mecânica quântica é:

\(\begin{aligned} \langle S_{\mathrm{qu\hat{a}ntico}}\rangle & =\quad\langle a_Ab_B\rangle+\langle a_Ab_B^{\prime}\rangle+\langle a_A^{\prime}b_B\rangle-\langle a_A^{\prime}b_B^{\prime}\rangle \\ & =\quad\langle a\cdot b+a\cdot b^{\prime}+a^{\prime}\cdot b-a^{\prime}\cdot b^{\prime} \end{aligned}\) (7)

Para maximizar este valor, podemos escolher as direções dos vetores unitários de forma estratégica. Uma escolha comum é:

• \(a\) ao longo do eixo \(x\) (ângulo \(0\)°): \(a=(1,0)\),
• \({a}'\) ao longo do eixo \(y\) (ângulo \(90\)°): \(a^{\prime}=(0,1)\),
• \(b\) a \(45\)° do eixo \(x{:}b=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\),
• \({b}'\) a \(-45\)° do eixo \(x{:}{b}'=\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)\)

Substituindo estes valores na expressão para \(\langle S_{\mathrm{qu\hat{a}ntico}}\rangle\):

\(\langle S_{\mathrm{qu\hat{a}ntico}}\rangle=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\left(-\frac{1}{\sqrt{2}}\right)=\frac{4}{\sqrt{2}}=2\sqrt{2}\)

O valor máximo para a mecânica quântica é:

\(\langle S_{\mathrm{qu\hat{a}ntico}}\rangle=2\sqrt{2}\approx2,828\)

6. Conclusão: Violação da Desigualdade de Bell.

Comparando os dois resultados, obtemos:

• Realismo Local: \(|\langle S_{\mathrm{cl\acute{a}ssico}}\rangle|\leq2\)
• Mecânica Quântica: \(\left|\langle S_{\mathrm{qu\hat{a}ntico}}\rangle\right|=2\sqrt{2}\approx2,828\)

Claramente, \(2\sqrt{2}>2\).

Isso significa que as previsões da mecânica quântica violam a Desigualdade de Bell.

Experiências reais, iniciadas por John Clauser e Stuart Freedman nos anos 70, e melhoradas significativamente por Alain Aspect nos anos 80, e por muitos outros desde então (com “loopholes” cada vez menores), confirmaram consistentemente as previsões da mecânica quântica, obtendo valores próximos de \(2\sqrt{2}\), violando o limite clássico de .

A violação da Desigualdade de Bell implica que a nossa intuição de realismo local é falsa. Portanto, pelo menos uma das premissas do realismo local deve ser falsa:

• Ou o realismo é falso: As propriedades das partículas não são predeterminadas antes da medição, mas sim criadas — tornam-se definidas apenas quando medidas.
• Ou a localidade é falsa: Há uma “ação fantasmagórica à distância”, uma influência instantânea entre as partículas entrelaçadas, mesmo separadas por grandes distâncias. As medições de Alice podem influenciar instantaneamente o estado da partícula de Bob, mesmo que estejam a anos-luz de distância.

A maioria dos físicos concorda que é a localidade que é violada, embora sem permitir comunicação de informação mais rápida do que a luz. A correlação é instantânea, mas o conteúdo informativo dessa correlação só pode ser verificado após a comunicação clássica dos resultados.

O universo quântico é intrinsecamente mais estranho e interconectado do que a física clássica nos levaria a crer. O entrelaçamento não é uma falha da teoria quântica; é uma de suas características mais fundamentais e contraintuitivas, que a natureza de facto exibe.

A Desigualdade de Bell transformou a metafísica quântica em física experimental, revelando que a realidade em seu nível mais fundamental opera de maneiras que desafiam profundamente a nossa compreensão diária.