O próprio Dirac estudou as experiências descritas abaixo, e relatou as suas conclusões no livro “The principles of quantum mechanics”⁶. Esclarece três pontos importantes. O primeiro é que a descrição quântica nos diz que um fotão pode estar em vários estados simultaneamente, no sentido discutido mais abaixo. A interpretação quântica traz-nos, portanto, este fenómeno contraintuitivo, sem oferecer uma descrição do que se passa ao nível de um fotão individual (está “num estado e noutro”? Num “estado ou noutro”?). No entanto, Dirac argumenta que o trabalho da ciência não é oferecer uma história, ou ilustração, mas de descrever fenómenos naturais. No segundo ponto, Dirac comenta que apesar desta experiência ser simples e da interpretação quântica não trazer nada de mais em termos de previsões, é uma boa maneira de ganhar intuição sobre como a mecânica quântica funciona. Finalmente, o autor comenta que tentarmos abstrair-nos do determinismo da física clássica pode levar-nos a situações paradoxais, ou no mínimo, pouco intuitivas. Neste artigo, vamos explicar em detalhe os argumentos de Dirac, mostrando de facto que esta experiência tem valor pedagógico no que toca a explicar a mecânica quântica.

Princípio de superposição.

O princípio de sobreposição, formulado primeiramente por Dirac, é uma forma de dizer que, para prever as correlações observadas no mundo quântico, nós precisamos de todos os vetores que descrevem o espaço de situações fisicamente possíveis, os observáveis, e a sobreposição desses vetores também corresponde a uma solução para dois ou mais estados quânticos. Matemáticamente, este princípio resulta da linearidade da equação de Schrödinger.

O primeiro ponto do Dirac é que o facto desta experiência poder ser descrita classicamente não reduz o interesse na sua descrição quântica. De facto, o trabalho da física é oferecer histórias/ descrições que corroborem a realidade experimental. Ter várias interpretações para uma experiência e poder compará-las é de grande valor pedagógico. Realmente hoje em dia a mecânica quântica é muito bem compreendida, ao ponto de sermos capazes de criar nova tecnologia baseada nela. No entanto, a interpretação do que a mecânica quântica nos diz sobre a realidade é fonte inesgotável de discussões entre matemáticos, físicos e filósofos.

Comecemos pela base: esta experiência é baseada numa propriedade da luz, a chamada polarização. A polarização da luz é uma característica física da radiação com uma interpretação “clássica” baseada no eletromagnetismo. Por exemplo, no caso de luz polarizada linearmente, descrevemos a luz como uma onda que oscila numa só direção do espaço, tal como na FIGURA 1. Classicamente, se uma onda polarizada verticalmente atravessa um polarizador orientado a 45°, a interpretação clássica consiste em dizer que metade da onda passa, metade é refletida ou absorvida. No entanto, se a luz é constituída de partículas, a partícula ou passa ou não passa. A interpretação do que acontece microscopicamente é o que chamaremos a interpretação “quântica”.

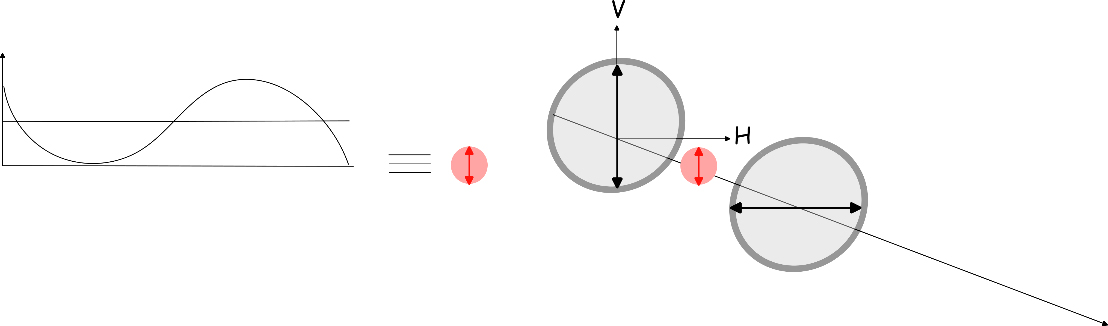
As duas interpretações permitem explicar o “aparente paradoxo dos três polarizadores” atendendo à lei de Malus^{1, 2}. O “paradoxo” é baseado na comparação de duas experiências: 1) uma cascata de dois polarizadores, orientados a 90° um do outro, 2) uma cascata de três polarizadores, o primeiro e o terceiro com uma orientação relativa de 90°, e o segundo introduzido com uma orientação de 45° relativamente ao primeiro e ao terceiro polarizador. Na primeira experiência, a luz não passa através da sequência de polarizadores. Poderíamos, ingenuamente, assumir que o que um polarizador faz é apenas bloquear a luz. No entanto, ao introduzirmos o terceiro polarizador entre os dois primeiros, vemos luz à saída da cascata! Nesse caso, perdemos 25% da intensidade da luz. Se introduzirmos o polarizador a 45° antes ou depois de dois polarizadores a 90°, não observamos luz.

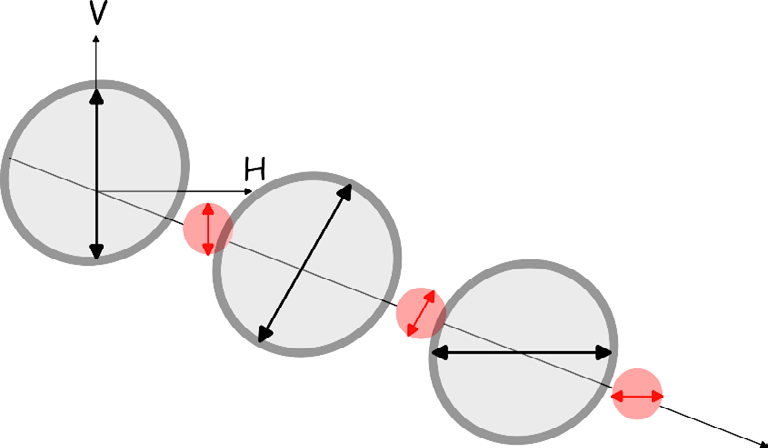
A interpretação clássica diz-nos o seguinte. Ao passar pelo polarizador 1, perdemos metade da luz, porque esta, sendo não-polarizada, contém uma mistura igual de luz polarizada horizontal e verticalmente. A luz estando agora polarizada verticalmente, contém luz polarizada a 45 graus e luz polarizada a -45° em quantidades iguais, portanto ao passar no polarizador 2 perdemos novamente metade da luz. E o mesmo acontece com o polarizador 3. Portanto no final ficamos com 12.5% intensidade de luz inicial. Se o ângulo for menor, perde-se menos luz. Portanto se tivermos uma série infinita de polarizadores, teremos uma transmissão cada vez mais perto de 50%, isto porque o primeiro polarizador retira 50% da luz. Alternativamente, podemos considerar que a intensidade inicial de luz é a intensidade a seguir ao primeiro polarizador, nesse caso com a série infinita teremos 100% da luz a passar.

No caso microscópico, uma partícula ou passa por um polarizador, ou não passa. Temos, portanto, não uma intensidade de luz à saída, mas uma probabilidade de observar um fotão à saída da cascata de polarizadores. A teoria da física quântica não nos oferece uma descrição “direta” do que se passa com cada partícula, mas permite-nos calcular as probabilidades com precisão. Como fazer sentido da interpretação quântica desta experiência?

Dois ingredientes básicos da mecânica quântica são os estados das partículas, que especificam a informação contida num sistema físico, e as medições (observações). As medições: 1) Extraem informação sobre o estado da partícula, 2) perturbam o estado, transformando-o.

Consideremos cada fotão incidindo nos polarizadores. Os polarizadores assumem o papel de observações, ou medições. Especificamente, podemos imaginar que o fotão está em dois estados possíveis, cada um com a sua probabilidade, um alinhado com o angulo do polarizador, e um perpendicular. Ao chegar ao polarizador, o fotão ou assume o estado alinhado com o polarizador e muda de polarização (salto quântico), ou adota o estado perpendicular e é absorvido. Este processo é uma medição quântica. Medições a nível quântico perturbam, portanto, o estado da partícula. Isso é intuitivo: se eu tentar observar algo tão frágil como uma partícula, vou perturbá- -la. Portanto o polarizador altera o estado do fotão aquando da sua passagem, de facto o fotão assume um estado polarizado alinhado com o polarizador pelo qual passou. A perturbação do estado será maior se o ângulo entre o estado do fotão e o ângulo do polarizador fôr maior. Ao introduzirmos o terceiro polarizador, fazemos com que a perturbação seja menor a cada passagem pelo polarizador, o que leva à saída de uma maior quantidade de luz. Se introduzirmos múltiplos polarizadores, reduzindo o ângulo relativo entre os dois polarizadores, conseguiremos aumentar a quantidade de luz transmitida.

O primeiro polarizador cria o estado inicial: vertical por exemplo. O último polarizador, com o detetor de luz, constitui uma medição final, no fundo uma pergunta: “o fotão está no estado horizontal?”. A resposta é “sim” se repetirmos a experiência e observarmos um fotão à saída desse polarizador com 100% de probabilidade. Se tivermos só dois polarizadores orientados a 90 graus, o estado inicial será vertical, e, portanto, a resposta à medição final é “não” com 100% de probabilidade, visto que os estados são ortogonais. Se tivermos mais polarizadores entre o primeiro e o último, esses polarizadores vão agir como uma medição “fraca” (ângulo pequeno) e vão rodando o estado. Quanto mais polarizadores, o ângulo relativo entre o último e o penúltimo polarizador torna-se tão pequeno que a luz é efetivamente horizontal aquando da medição final. O facto de perturbar pouco, tendo múltiplos polarizadores com ângulos pequenos, implica que a perturbação no estado dos fotões é pequena, o que explica porque conseguimos ter uma transmissão de 100% para um número infinito de polarizadores. No fundo, rodámos polarização do fotão sem o destruir. Este tipo de medições chama-se medição quântica não-destrutiva, e tem aplicações muito interessantes, tais como analisar sistemas biológicos com luz, suscetíveis de serem danificados ao absorverem demasiada luz.

A interpretação quântica.

Vamos descrever o estado de polarização da luz como um vetor bi-dimensional, tal como ilustrado na FIGURA 3. Luz polarizada verticalmente corresponde a um vetor que aponta para cima \((0,1)\), e se for horizontal corresponde a \((1,0)\). Usamos a notação de Dirac para representar estes vetores, \(\left|V\right\rangle\) e \(\left|H\right\rangle\) respetivamente. Um vetor arbitrário escreve-se

\(\left|\alpha\right\rangle=\cos\left.\alpha\left|H\right\rangle+\sin\left.\alpha\left|V\right\rangle\right.\right.\)

A mecânica quântica explica como calcular: 1) a probabilidade de transmissão destes estados através de um polarizador, e 2) o estado à saída do polarizador. Aquando da passagem do estado \(\left|V\right\rangle\)\) pelo segundo polarizador, orientado a 45°, temos que:

1. A probabilidade de transmissão é dada por

\(P=\left|\left\langle V\left|P\left(45^\circ\right)\right|V\right\rangle\right|^2=\frac{1}{2}\)

onde \(P\left(45^{\circ}\right)=\left|45^{\circ}\right\rangle\left<45^{\circ}\right|\).

2. O estado à saída é o estado orientado a 45°, ou seja, \(\alpha=\)45°. Em linguagem mais formal, diz-se que a medição projeta o estado quântico para o estado alinhado a 45°,

\(|45^\circ\rangle=1/(|H\rangle+|V\rangle)\sqrt{2}\)

Podemos continuar o exercício e calcular a probabilidade de transmissão através do filtro final, orientado a 90°, ou seja, correspondendo a um estado \(|H\rangle\). Esta é dada por,

\(\textrm{Prob}=\cos^2(45^{\circ}-\theta_2)\)

As regras da mecânica quântica explicam exatamente o comportamento observado na experiência. No entanto, as observações podem parecer contraintuitivas, sobretudo por duas razões:

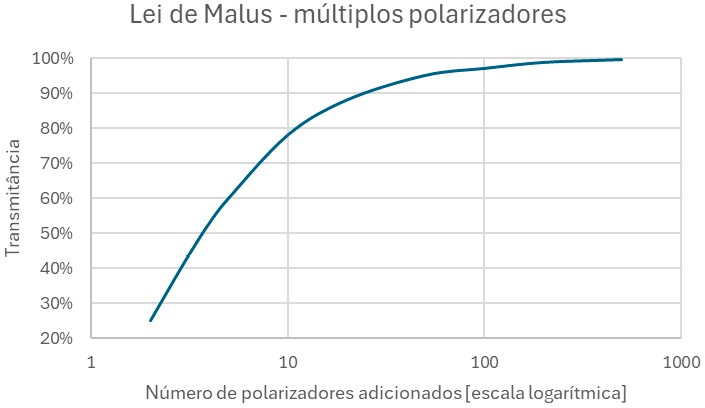
1. A não linearidade da probabilidade de transmissão: Os polarizadores só reduzem a quantidade de luz, e por essa razão poderíamos ingenuamente pensar que a redução de luz deve ser linear, ou seja, proporcional ao ângulo do segundo polarizador. Não é o caso. Para o ver, partimos de novo de um estado \(|V\rangle\). Se o segundo polarizador estiver orientado a 45°, já vimos que 50% da luz será transmitida (normalizando à intensidade da luz a seguir ao primeiro polarizador). Seria natural imaginar que se colocarmos um polarizador adicional antes do polarizador a 45°, à saída veríamos 25% da luz. Ao contrário, a mecânica quântica nesse caso prevê que teremos mais de 50% da luz a ser transmitida. Isto deve-se ao facto da probabilidade de transmissão ser uma função não-linear do ângulo. No entanto, esta propriedade não é especificamente quântica, também se pode deduzir da teoria das ondas. Uma consequência interessante é que se colocarmos mais filtros entre os ângulos dos polarizadores já instalados, tal como ilustrado na FIGURA 3, a probabilidade de transmissão vai aumentando com o número de filtros, tendendo para 1, como o demonstra a FIGURA 4.

2. A segunda questão contraintuitiva é mais profunda, e tem a ver com a relação entre o observador e a partícula, a noção de realidade, e o determinismo. A mecânica quântica é uma teoria estatística no sentido em que nos permite prever a probabilidade de observar algum fenómeno numa partícula, não oferece uma história do que acontece a cada partícula. Por exemplo, o fotão, vendo o segundo polarizador, decide se será transmitido no terceiro? Ou será que o fotão já tem a informação de como se comportar antes da experiência acontecer? Procuramos uma interpretação mais detalhada das previsões da mecânica quântica! Podemos tentar responder a esta questão formalmente, usando o conceito de variáveis escondidas. Estas variáveis matemáticas existiriam para descrever o mundo partícula a partícula.

O mundo microscópico, descrito pela física quântica, parece ser não determinista. Ou seja, quando fazemos uma medição (pergunta) de um fotão, o resultado (resposta) é fundamentalmente aleatório. Isso quer dizer que não sabemos descrever o que levou o fotão a passar ou não pelo polarizador. Esta experiência permite-nos refletir sobre a possibilidade da Natureza ser determinista, no sentido em que as respostas que cada medição fornece sobre cada partícula estarem pré-determinadas antes da experiência acontecer.

No caso desta experiência, e em geral nos sistemas individuais, existe uma explicação determinista apesar de ela não ser óbvia. Na verdade, é sempre possível oferecer uma explicação determinista para os resultados da mecânica quântica, usando as chamadas teorias de variáveis escondidas. Para concluir, veremos numa situação mais complexa, mas semelhante à nossa experiência dos polarizadores, uma contradição entre física quântica e modelos de variáveis escondidas: a chamada experiência de Bell. Este físico irlandês, John Bell, levou a humanidade a questionar-se sobre o que é realidade física e localidade. A nossa experiência intui a experiência de Bell demonstrando que o universo não é determinista, introduzindo o conceito de não localidade quântica.

O próprio Einstein, em 1935¹, suspeitava que a mecânica quântica poderia estar incompleta, que lhe faltariam variáveis matemáticas adicionais, as tais variáveis escondidas. Estas variáveis adicionais costumam ser designadas por \(\lambda\). Se fosse o caso, as variáveis lambda explicariam de forma determinista o comportamento das partículas ao serem observadas.

Na nossa experiência é possível ter uma explicação pré-determinada (com variáveis escondidas) do que ocorreu. Por exemplo, no caso dos primeiros dois polarizadores estarem orientados a 0°, basta o fotão “escolher” ser transmitido com a probabilidade correspondendo à da mecânica quântica. Para o ver, supomos que a partícula tem consigo um gerador de números aleatórios e um guia de marcha. Esse gerador gera 0 ou 1 com as probabilidades que quisermos, podemos escolher: por exemplo 20% e 70%, respetivamente. No guia de marcha a partícula tem as instruções de como se comportar: quando o gerador diz 0, a partícula escolhe ser transmitida, quando dá 1, escolhe ser absorvida/refletida. No caso dos dois primeiros polarizadores estarem orientados a 0° e 45° respetivamente, a questão é se o fotão podia saber como reagir dependendo do segundo filtro estar lá ou não, e reproduzir os resultados da mecânica quântica. A resposta continua a ser sim, basta a partícula conhecer as probabilidades que tem de reproduzir e repetindo-se a experiência, vai mudando o seu comportamento conforme o segundo polarizador lá está ou não. Nesse sentido, a resposta do fotão à situação experimental estaria pré-determinada, por exemplo aquando da criação dessa partícula, ou mesmo aquando da criação do universo (um conceito chamado super-determinismo).

Teorema de Bell.

O teorema de Bell prova que o universo não é local, no sentido em que um modelo local de variáveis escondidas local é incapaz de reproduzir os resultados da mecânica quântica. Um modelo ser local significa que não há influência à distância. Esse fenómeno está por detrás de muitos aspetos contraintuitivos da mecânica quântica, e também por detrás de diversas tecnologias quânticas.

Portanto sim, poderíamos imaginar que o comportamento da partícula está pré-determinado desde o momento da sua criação. Isso reproduziria todos os resultados da mecânica quântica baseados em experiências envolvendo uma partícula de cada vez. Será, portanto, que acabámos de descobrir uma teoria alternativa à mecânica quântica? A resposta é não! Mas teremos de complicar um pouco a história.

Portanto aparentemente podemos ter uma descrição determinista ou indeterminista da Natureza, ambos parecem funcionar. Poderíamos também pensar que modelos de variáveis escondidas são legítimos e descrevem a Natureza tão bem como a mecânica quântica. Nesse caso, os modelos de variáveis escondidas poderiam oferecer-nos uma perspetiva da realidade mais alinhada com a nossa intuição clássica. No entanto, não é o caso, uma teoria de variáveis escondidas não descreve a realidade se introduzirmos mais um conceito: a ideia de localidade. Intuitivamente, localidade significa que dois sistemas distantes não se podem influenciar instantaneamente. No entanto, sistemas de várias partículas podem exibir correlações quânticas que não podem ser explicadas por um modelo de variáveis escondidas obedecendo ao princípio de localidade. Este resultado fundamental é chamado o teorema de Bell, que diz que a mecânica quântica é nãolocal.

O exemplo dos três polarizadores serve para introduzir a possibilidade de existirem variáveis que possam suplementar a mecânica quântica, de forma a dar-nos uma explicação intuitiva do que acontece, partícula a partícula. Na experiência dita de Malus não existe atrito entre teorias com variáveis suplementares e mecânica quântica, mas se considerarmos sistemas quânticos com mais de uma partícula, já não é o caso. De facto, com duas partículas ou mais, a mecânica quântica não pode ser reproduzida por teorias com variáveis suplementares. Essas teorias são chamadas teorias de variáveis suplementares locais. Locais, porque, como temos várias partículas, temos adicionalmente de supôr que elas não podem comunicar entre si instantaneamente (não conhecemos nada no universo que o faça!). Como a mecânica quântica entra em conflito com modelos locais de variáveis escondidas, dizemos que ela é “não local”. Isso diz-nos que, se quisermos descrever o mundo partícula a partícula, teremos de abandonar a noção de localidade. Esta é a mensagem do teorema de Bell⁵, do físico John Bell, que mudou radicalmente a nossa perspetiva de como a Natureza processa informação.