Neste artigo, discutiremos o “mistério quântico” seguinte — a existência (ou não) na Natureza de ações instantâneas fantasmagóricas (spooky) à distância. Foi assim que Albert Einstein as designou no famoso artigo “Can Quantum Mechanical Description of Physical Reality Be Considered Complete?“, publicado em colaboração com Boris Podolsky, e Nathan Rosen, na revista Physical Review, em 1935.

Mas o que significa “ação” neste contexto? Se existem estas ações, em que consistem? Numa transferência instantânea de matéria?, numa transferência instantânea de energia?, numa transferência instantânea de mensagens?, ou numa transferência instantânea de informações? Além disso:

• Se existem ações instantâneas à distância, isso não contradiz a ideia de que “nada pode andar mais rápido do que a luz “, como afirma a teoria da relatividade?
• Se a mecânica quântica mostra que a mente age diretamente sobre a matéria, tais ações à distância permitem a telepatia?

1. Entrelaçamento quântico.

A sobreposição quântica é um mistério. Porque é que o estado quântico de uma partícula há-de ser uma sobreposição linear de estados? Acontece que a mecânica quântica tem ainda outro mistério — aquele que ocorre como consequência de estados de sobreposição que envolvem duas ou mais partículas — o chamado Entrelaçamento quântico, que é como vamos traduzir a designação inglesa “Quantum Entanglement”.

Experiência motivadora.

Vamos começar com um exemplo simples, para motivar a discussão. Imaginemos o seguinte:

Temos duas caixas idênticas, fechadas e lacradas. Dentro de uma dessa caixas está uma bola preta e dentro da outra está uma bola branca. Ninguém sabe qual a caixa que contém a bola preta e qual a que contém a branca. E o mais importante — a mecânica quântica sugere que, na verdade, a cor da bola em cada caixa não está definida até que alguém abra a caixa e observe a côr da bola lá contida. É como se cada bola estivesse numa espécie de “névoa” (sobreposição) de ser preta e branca ao mesmo tempo, mas de tal forma que as duas bolas (uma em cada uma das duas caixas) têm sempre cores opostas.

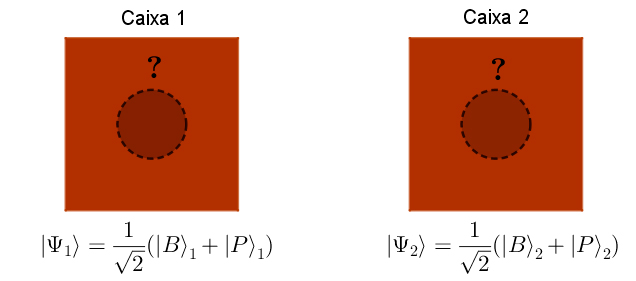
Mas se a bola de cada caixa está numa sobreposição de branca e preta, o que significa dizer que têm sempre cores opostas?

Boa pergunta! A resposta vai permitir perceber melhor o que está em jogo, e porque é o entrelaçamento é tão contra-intuitivo, mas ao mesmo tempo tão fascinante!

A chave para a resposta está em como descrevemos o estado do PAR de caixas (ou partículas), e não apenas o estado de cada caixa individualmente (FIGURA 1). De facto, no momento em que as caixas são preparadas, o par de bolas está num estado específico — elas têm cores opostas. Essa é a correlação que está “embutida” no sistema desde o início. Quando falamos de sobreposição, estamos a dizer que o PAR está numa sobreposição de duas possibilidades (estados):

• Possibilidade 1: Caixa 1 tem Bola Preta e Caixa B tem Bola Branca
• Possibilidade 2: Caixa 2 tem Bola Branca e Caixa B tem Bola Preta.

O estado do PAR é uma “mistura” ou “névoa de possibilidades” dessas duas opções (FIGURA 2). Ambas as possibilidades existem simultaneamente até ao momento da medição. O PAR de caixas e bolas formam pois um sistema conjunto que está numa sobreposição de duas possibilidade correlacionadas.

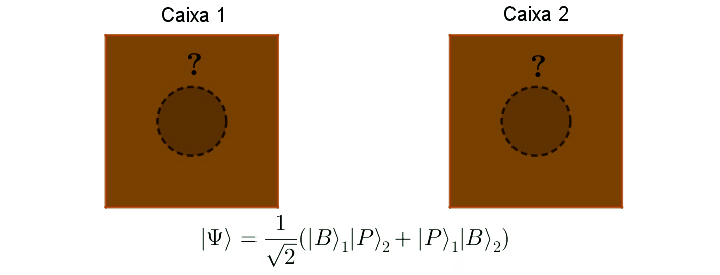
Isto é completamente diferente de dizer que “a Caixa 1 tem bola preta e branca” e “Caixa 2 tem bola preta e branca”. Mais à fente seremos mais formais ao descrever esta diferença crucial.

Portanto, a frase “têm sempre cores opostas “, refere-se à correlação fundamental que define o estado entrelaçado do PAR. A sobreposição refere-se ao facto de que, individualmente, as cores não estão definidas antes da medição. É a sobreposição dessas combinações correlacionadas que faz o entrelaçamento ser tão peculiar.

Alice abre a sua caixa...

Agora Alice leva uma das caixas para Marte. Chamemos a essa caixa \(C_1\). Bob fica com a outra caixa — a caixa \(C_2\) — que leva para uma galáxia distante. Alice e Bob não têm qualquer forma de se comunicarem entre si. Quando Alice abre a sua Caixa \(C_1\), o que acontece? Ou ela vê uma bola branca ou vê uma preta, é claro.

Se ela vê que a bola na sua caixa é Preta, então o acto de abrir a caixa “forçou” o sistema a escolher a possibilidade 1: “Caixa 1 tem Bola Preta e Caixa B tem Bola Branca”. Instantaneamente, a “névoa” das possibilidades colapsa, e agora Alice sabe, com 100% de certeza, que a Caixa de Bob, tem Bola Branca.

Mas atenção: Bob, na sua galáxia, não sabe nada sobre a côr da Bola da sua caixa, que continua fechada. Por isso, para Bob, a bola na sua caixa ainda é uma sobreposição de Preta e Branca. Bob não ganhou nenhuma informação sobre a cor da sua bola, pelo facto de Alice ter aberto a sua e já saber qual a côr da Bola que está na caixa de Bob. Bob só saberá a côr da sua bola quando abrir a sua caixa.

Enfim: a ação fantasmagórica à distância!

A “ação fantasmagórica à distância” (Spooky Action at a Distance), que era o inquietava Einstein, não diz que Bob sabe instantaneamente a cor da sua bola, quando Alice abre a sua caixa. Este é um erro que às vezes se lê em alguns livros!

A bola de Alice NÃO ERA Preta antes de ela abrir a sua caixa. Este acto (de medição) é que fez a sua bola tornar-se Preta. E, de alguma forma inexplicável, instantaneamente (sem qualquer tipo de comunicação superluminal), o acto de Alice medir a côr da sua bola (abrindo a sua caixa) forçou a bola de Bob a definir-se como BRANCA. Ou seja, a ação é no estado físico da bola de Bob. O seu estado foi instantaneamente determinado pela medição de Alice, mesmo que Bob não saiba disso até que ele mesmo a meça. É o colapso do estado da caixa distante, não a transferência de informação.

Einstein achava isso inaceitável porque implicava que a realidade de algo distante é determinada pela observação local, sem uma conexão física aparente. O “fantasmagórico” reside nessa determinação instantânea do estado físico de um objeto distante, sem que haja qualquer sinal mediador viajando entre eles. Isso parecia desafiar as noções a que estamos (por demais) habituados — a noção de causalidade e a de localidade.

2. Exposição formal.

Suponhamos que temos duas caixas fechadas e lacradas: \(C_1\) e \(C_2\). Cada uma contem uma bola que pode ser Branca ou Preta. O estado da caixa define-se pela côr da bola que contém. Assim a caixa \(C_1\) pode estar num de dois estados (puros), \(|B\rangle_1\) ou \(|P\rangle_1\) ou numa sobreposição desses dois estados:

\(|C_{1}\rangle=\alpha|B\rangle_{1}+\beta|P\rangle_{1},\quad\alpha,\beta\in\mathbb{C},|\alpha|^{2}+|\beta|^{2}=1\)

e o mesmo acontece para a caixa \(C_2\)

\(|C_{2}\rangle=\gamma|B\rangle_{2}+\delta|P\rangle_{2},\quad\gamma,\delta\in\mathbb{C},|\gamma|^{2}+|\delta|^{2}=1\)

(Ver a FIGURA 1).

Como dissémos acima, quando consideramos o sistema conjunto constituído pelo PAR de caixas \(C_1\) e \(C_2\), podemos facilmente listar os respetivos estados, usando uma espécie de produto:

\(|B|_{1}|B\rangle_{2},\quad|B\rangle_{1}|P\rangle_{2},\quad|P\rangle_{1}|B\rangle_{2},\quad|P\rangle_{1}|P\rangle_{2}\) (1)

ou qualquer sobreposição quântica destes:

\(|C_{1}C_{2}\rangle=\alpha|B\rangle_{1}|B\rangle_{2}+\beta|B\rangle_{1}|P\rangle_{2}+\gamma|P\rangle_{1}|B\rangle_{2}+\delta|P\rangle_{1}|P\rangle_{2}\) (2)

com \(\alpha\), \(\gamma\), \(\lambda\in\mathbb{C}\), com \(|\alpha|^{2}+|\beta|^{2}+|\gamma|^{2}+|\delta|^{2}=1\). Os estados (1), são chamados estados produto (tensorial), porque podemos especificar, de forma independente, o estado de cada caixa, e depois multiplicá-los para obter o estado do sistema do PAR de caixas, escrito na forma:

\(|\text{estado da caixa }C_1\rangle|\text{estado da caixa }C_2\rangle\) (3)

Um exemplo de um estado de sobreposição quântica, (2), do PAR de caixas é

\(|C_{1}C_{2}\rangle=\frac{1}{\sqrt{2}}(|B\rangle_{1}|B\rangle_{2}+|P\rangle_{1}|B\rangle_{2})\) (4)

Este estado é um estado produto, já que pode ser separado, ou factorizado, na forma:

\(|C_1C_2\rangle=|C_1\rangle|C_2\rangle=\frac{1}{\sqrt{2}}(|B\rangle_1+|P\rangle_1)|B\rangle_2\) (5)

o que significa que a caixa 1 está num estado de sobreposição quântica de branco e preto, enquanto que a caixa 2 está no estado branco. Mais detalhadamente, o significado da equação (5) das duas partículas é o seguinte:

• A bola da caixa \(C_1\) exibe indefinição objetiva em relação aos estados branco e preto — a probabilidade de ser medida como branca é igual a 1/2, a probabilidade de ser medida como preta é também igual a 1/2, enquanto que
• A caixa 2 será sempre branca com probabilidade 1, após medição.

Não há correlação entre os resultados obtidos para as duas caixas. O estado do sistema conjunto, constituído pelas duas caixas, pode ser escrito como um produto do estado de cada uma das caixas e, por isso, o sistema diz-se separável, o que significa que o estado de cada caixa é inteiramente independente do da outra.

Consideremos agora o estado EPR seguinte

\(|C_{1}C_{2}\rangle=\frac{1}{\sqrt{2}}(|B\rangle_{1}|P\rangle_{2}+|P\rangle_{1}|B\rangle_{2})\) (6)

O seu significado é o seguinte: a probabilidade de encontrar O PAR de caixas com bolas de côr oposta é igual a 1/2. As duas caixas estão assim firmemente correlacionadas : ou a caixa \(C_1\), quando aberta (ou medida) mostrará a bola Branca, e, portanto, a caixa \(C_2\) quando medida (ou aberta) mostrará a bola preta, ou a caixa \(C_1\), quando aberta (ou medida) mostrará a bola Preta, e, portanto, a caixa \(C_2\) quando medida (ou aberta) mostrará a bola Branca. Nunca temos duas brancas ou duas pretas.

Além disso, não é possível, ao contrário do caso anterior (4), escrever este estado como um produto dos estados de cada uma das caixas. Simbolicamente,

\(\begin{aligned} |C_1C_2\rangle\quad & =\quad\frac{1}{\sqrt{2}}(|B\rangle_1|P\rangle_2+|P\rangle_1|B\rangle_2 \\ & \neq\quad|\text{estado da caixa }1\rangle\otimes|\text{estado da caixa }2\rangle \end{aligned}\) (7)

\(|C_{1}C_{2}\rangle\) é, neste caso, NÃO separável — diz-se, por isso, entrelaçado, e diz-se que o PAR de caixas, como sistema conjunto, está num estado de entrelaçamento quântico.

Vamos ser mais concretos. Assim, suponhamos que Alice abre a sua caixa, \(C_1\), para medir a Côr da bola que está lá dentro. Suponhamos que ela obtem a Côr branca, \(|B\rangle_1\), com probabilidade 1/2. Pela Regra de Born, o estado entrelaçado \(|C_{1}C_{2}\rangle\), sofre o colapso

\(|C_1C_2\rangle\xrightarrow{\text{Alice mede a cor da sua bola}}|B\rangle_1|P\rangle_2\) (8)

Quando Bob mede a Côr da sua bola (abrindo a sua caixa \(C_2\)), não se depara com qualquer ambiguidade — a sua bola é preta, com certeza absoluta!

\(\left|B\right\rangle_{1}\left|P\right\rangle_{2}\xrightarrow{\text{Bob mede a cor da sua bola}}\left|P\right\rangle_{2}\) (9)

Portanto, temos a sequência de medições e colapsos seguinte:

\(|C_1C_2\rangle\xrightarrow{\text{Alice mede a cor da sua bola}}|B\rangle_1|P\rangle_2\xrightarrow{\text{Bob mede a cor da sua bola}}|P\rangle_2\)

A meneira usual de descrever isto, é dizer que o estado da caixa de Bob, \(C_2\), foi projetada no estado \(|P\rangle_2\), pela medição feita por Alice na sua caixa \(C_1\). Veja a segunda FIGURA 4.

Mas isto acontece, não porque a caixa \(C_2\) tenha bola preta antes de medir a bola da caixa \(C_1\), mas sim porque, a medição de \(C_1\), deu instantaneamente à bola de \(C_2\) uma Côr determinada, que não tinha antes da medição de \(C_1\). Mais ainda, esta côr da bola de \(C_2\) só é detectável quando a caixa é aberta por Bob.

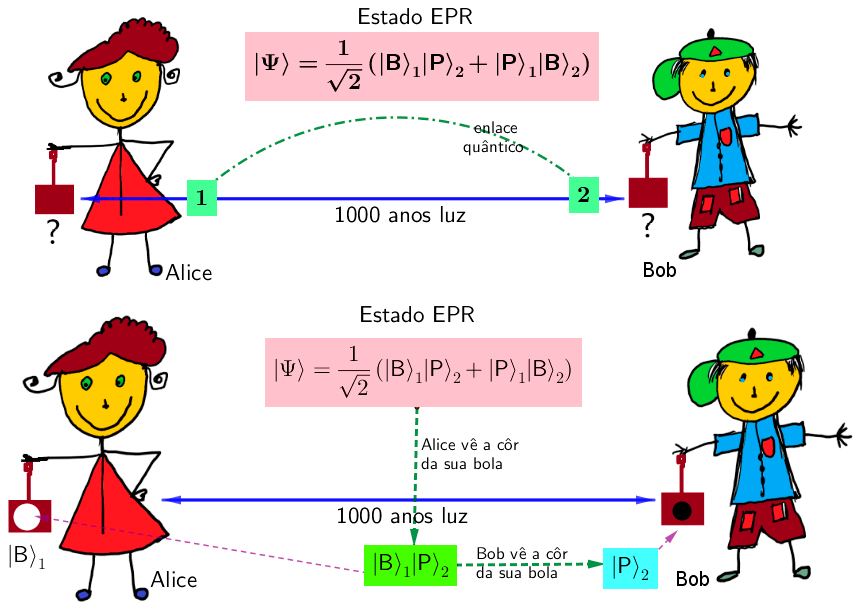
Considerações completamente análogas podem ser feitas, se medirmos a Côr da caixa \(C_1\), obtendo o resultado \(|P\rangle_1\), com probabilidade 1/2. Neste caso, o estado final do sistema composto será \(|P\rangle_1|B\rangle_2\) e, portanto, a bola da caixa \(C_2\), quando medida, é branca com certeza absoluta.

\(|C_1C_2\rangle\xrightarrow{\text{Alice mede a cor da part\'{ı}cula}1}|P\rangle_1|B\rangle_2\xrightarrow{\text{Bob mede a cor da part\'{ı}cula}2}|B\rangle_2\)

Bom! Se tudo isto é verdade, NÃO mostramos que existem ações instantâneas à distância. Einstein chamou-lhes assustadoras (“spooky actions”) porque, se existissem, se “propagariam” com “velocidade infinita”. De facto, quando Alice abre a sua caixa e vê que a bola lá dentro é, por exemplo, preta, Bob NÃO fica a saber instantaneamente que a Côr da bola da sua caixa é branca, antes de a observar ! SÓ depois de abrir a sua caixa é que Bob fica a saber que a Côr da sua bola é Branca! Claro que Alice sabe isso, antes da medição de Bob. Mas, como se disse acima, esse conhecimento de Alice não informa nada a Bob. Ou seja, a ação é no estado físico da bola de Bob, não na transferência de informação.

Portanto, o entrelaçamento quântico implica a existência destas ações instantâneas à distância, por maior que esta seja, MAS APENAS no sentido acima descrito. NÃO implica qualquer sinal que viaje mais depressa do que a luz. Não há pois qualquer contradição com o princípio básico da teoria da Relatividade: “nada se pode mover com uma velocidade superior à da luz “. Contraria sim o nosso senso comum de que uma influência é sempre de carácter local — objetos muito distantes não podem influenciar-se um ao outro.

A este propósito leia a seguinte notícia do Jornal Público, e comente algumas imprecisões que ela contem!

O Prémio Nobel da Física de 2022 foi atribuído aos investigadores em informação quântica, Alain Aspect, John F. Clauser e Anton Zeilinger, pelos seus contributos inovadores envolvendo estados quânticos enlaçados.

O entrelaçamento quântico diz, basicamente, que duas partículas podem comportar-se como uma unidade, mesmo quando estão separadas por uma longa distância. Por exemplo, para dois eletrões enlaçados, se sabemos as propriedades físicas de um, automaticamente saberemos as do outro. Esse facto, no qual a informação parece viajar mais rápido do que a luz, levou os cientistas a pensarem que a teoria quântica estava incompleta. A existência de variáveis ocultas, foi sugerida por alguns, como uma possível explicação para a correlação entre partículas enlaçadas. No entanto, em 1960, John Bell desenvolveu uma desigualdade matemática, agora chamada desigualdade de Bell, que permite concluir que, se de facto existirem variáveis ocultas, uma certa quantidade física nunca poderia exceder um certo valor.

John Clauser desenvolveu uma experiência concreta, a partir das ideias de Bell, cujos resultados violaram a desigualdade de Bell, provando assim que a mecânica quântica não pode ser substituída por uma teoria com variáveis ocultas. A contribuição de Alain Aspect foi modificar a configuração dessa experiência para que a configuração, no momento em que ele foi emitido, não interferisse nos resultados. Anton Zeilinger, com seu grupo de investigação, demonstrou a existência do fenómeno do teletransporte quântico…

O entrelaçamento é uma correlação intrínseca e fundamental entre as partes de um sistema.

O entrelaçamento é uma correlação intrínseca e fundamental entre as partes de um sistema.

Para “desfazer” o entrelaçamento, no sentido de tornar as partículas separáveis novamente, é preciso realizar uma medição no sistema, ou interagir o sistema com o ambiente.

O Efeito da Decoerência.

No mundo real, os sistemas quânticos nunca estão perfeitamente isolados. Eles interagem com o seu ambiente (outras partículas, campos, radiação). Essa interação tem como efeito um fenómeno chamado decoerência. A decoerência faz com que o entrelaçamento entre as duas partículas originais se “espalhe” para o ambiente. O entrelaçamento não é destruído, mas sim transferido para o sistema maior (partículas + ambiente), fazendo parecer que as partículas originais perdem as suas propriedades quânticas e se comportem classicamente. Para todos os efeitos práticos do nosso quotidiano macroscópico, o entrelaçamento entre as duas partículas específicas perde-se (ou torna-se inacessível).

O Universo é composto de objetos quânticos entrelaçados.

Será que estas correlações foram criadas no universo primordial (Big-Bang)? Esta é uma visão muito poderosa que encontra eco em muitas das teorias de vanguarda da física fundamental! A um nível fundamental, tudo no universo é quântico. As partículas interagem constantemente, e as interações podem levar ao entrelaçamento. Portanto, é razoável supor que há uma teia gigantesca e complexa de entrelaçamento subjacente a toda a realidade.

Muitos cosmólogos e físicos quânticos acreditam que as flutuações quânticas no universo primordial (logo após o Big Bang) são as “sementes” para a formação de todas as estruturas que vemos hoje, desde galáxias a estrelas e planetas. Essas flutuações eram, por natureza, quânticas e entrelaçadas.

As pequenas variações de temperatura na Radiação Cósmica de Fundo em micro-ondas (CMB) — a “radiação fóssil” do Big Bang — são a evidência observacional dessas flutuações primordiais. As correlações observadas nessas variações podem ser explicadas pela natureza quântica do universo primordial. Mas, à medida que o universo se expandiu e arrefeceu, ele passou por um processo massivo de decoerência. Esse processo fez com que as estruturas emergentes se tornassem cada vez mais clássicas, dando origem ao espaço-tempo e à matéria que descrevemos com a Relatividade Geral e a Mecânica Quântica (Teoria Quântica de Campos) em escalas maiores. Mas a “memória” dessas correlações primordiais, embora diluída e manifestada em propriedades emergentes, ainda pode estar lá.