A polarização da luz é uma característica física da radiação com uma interpretação “clássica” baseada no eletromagnetismo. Esta permite explicar o “paradoxo dos três polarizadores” atendendo à lei de Malus^{1, 2}, sendo o paradoxo baseado no efeito em cascata de três polarizadores. Começamos pelo caso de apenas dois polarizadores, orientados a 90° um em relação ao outro, bloqueando dessa forma a passagem de qualquer luz. O paradoxo surge ao introduzir um terceiro polarizador a 45°; (i) se for introduzido entre eles surge luz através do sistema, que emergirá atenuada de 25% mas (ii) se for colocado imediatamente antes ou após os dois polarizadores iniciais nenhuma luz emergirá no extremo do percurso óptico uma vez que os polarizadores consecutivos a 90° eliminarão a passagem de qualquer luz². Adicionalmente, este fenómeno de “repolarização” da luz tem necessariamente uma interpretação quântica melhor compreendida no limite de um fotão único. De facto, o conjunto de fotões que consegue atravessar o último polarizador constitui a intensidade medida pelo detector. Neste artigo e num artigo complementar (versãoteórica) fazemos a experiência dos três polarizadores, e tentaremos conciliar as interpretações clássica e quântica.

Descrevendo o problema de forma microscópica, em termos de cada fotão incidindo nos polarizadores, compreendemos que os polarizadores nos permitem responder a questões tais como “o fotão passou no polarizador?”. Portanto, podemos aqui colocar três perguntas que correspondem a saber se um determinado fotão passou por cada um dos polarizadores. Ao fazermos a experiência e observarmos a quantidade de luz que sai, estamos a observar as respostas dadas por cada partícula de luz.

A experiência no ELAB.

O elab é uma plataforma de acesso remoto a experiências reais, atualizada recentemente com um novo software, o Framework for Remote Experiments in Education⁴.

A experiência da polarização da luz permite medir a potência luminosa num alvo após a luz da fonte incoerente (um LED branco) atravessar um sistema de dois ou três polarizadores e estudar o efeito provocado na intensidade luminosa devido à orientação relativa desses polarizadores. Na FIGURA 1 podemos observar um esquema simplificado da experiência.

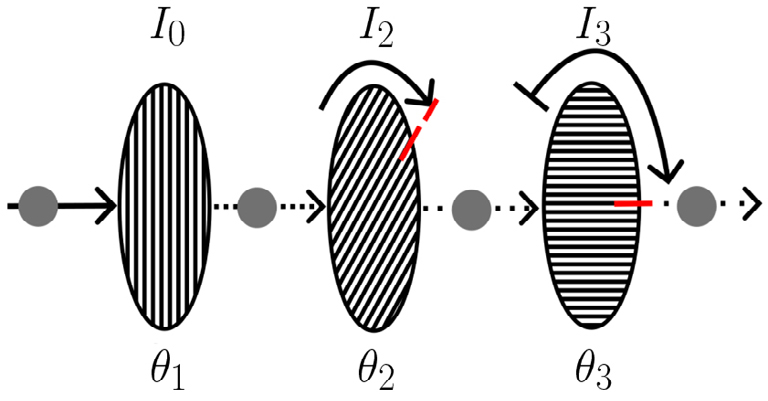
A intensidade da luz transmitida através de um par de polarizadores é regida pela lei de Malus, em função da intensidade da luz polarizada após o primeiro polarizador e do ângulo relativo entre os eixos de transmissão dos dois polarizadores. Para os primeiros dois polarizadores na FIGURA 1, temos

\(I_2=I_1\mathrm{cos}^2(\theta_2-\theta_1)\)

De forma semelhante, podemos aplicar sucessivamente a mesma lei para qualquer número de polarizadores. Para a configuração de três polarizadores da FIGURA 1, teremos

\(I_3=I_2\mathrm{cos}^2(\theta_3-\theta_2)=I_1\mathrm{cos}^2(\theta_2-\theta_1)\cos^2(\theta_3-\theta_2)\)

O primeiro polarizador apenas existe para criar um feixe de luz polarizada a 0° (vertical) se for ativado. De seguida, a luz atravessa um segundo polarizador cujo ângulo com a vertical é pré-definido entre -120° e 70°. Antes de incidir no sensor de luz baseado num fotodiodo, atravessa o último polarizador que pode efectuar um varrimento angular ligeiramente superior a 180°.

Caso se use à partida luz polarizada, pela configuração judiciosa da experiência, podemos replicar o paradoxo dos três polarizadores, e utilizando a lei de Malus comprovar a sua validade, usando a descrição da luz como uma onda electromagnética dotada duma polarização característica, ou seja o campo elétrico da onda oscila num plano determinado, perpendicular à direção de propagação da mesma.

O paradoxo dos três polarizadores.

Ao efectuar a experiência com luz polarizada (eliminando a componente energética da luz a 90°) e configurando o polarizador intermédio a 0°, -45° e -90° e de seguida fazendo um varrimento do terceiro polarizador entre -120° e 70° podemos observar resultados como os representados na FIGURA 2, com a inexpectável passagem de luz quando o último polarizador faz 90° com o primeiro!

Ou seja, quando o primeiro e o terceiro polarizadores estão a 90° entre si não passa qualquer luz (traço a verde) se o segundo estiver alinhado com o primeiro, mas estando o primeiro e terceiro a 90° (primeira linha tracejada) a luz consegue emergir após o terceiro polarizador na experiência com o polarizador intermédio a 45° (traço amarelo)!

No gráfico da FIGURA 2 estão traçadas as intensidades medidas pelo sensor de luz. Este gráfico permite determinar os erros sistemáticos existentes da montagem, pois (i) o máximo não se alinha rigorosamente aos 0°, antes a cerca de -2.7° devido à incerteza do posicionamento do primeiro filtro e (ii) devido à luz ambiente, existe sempre um valor não nulo medido pela fotocélula (inferior a 50 unidades de medida).

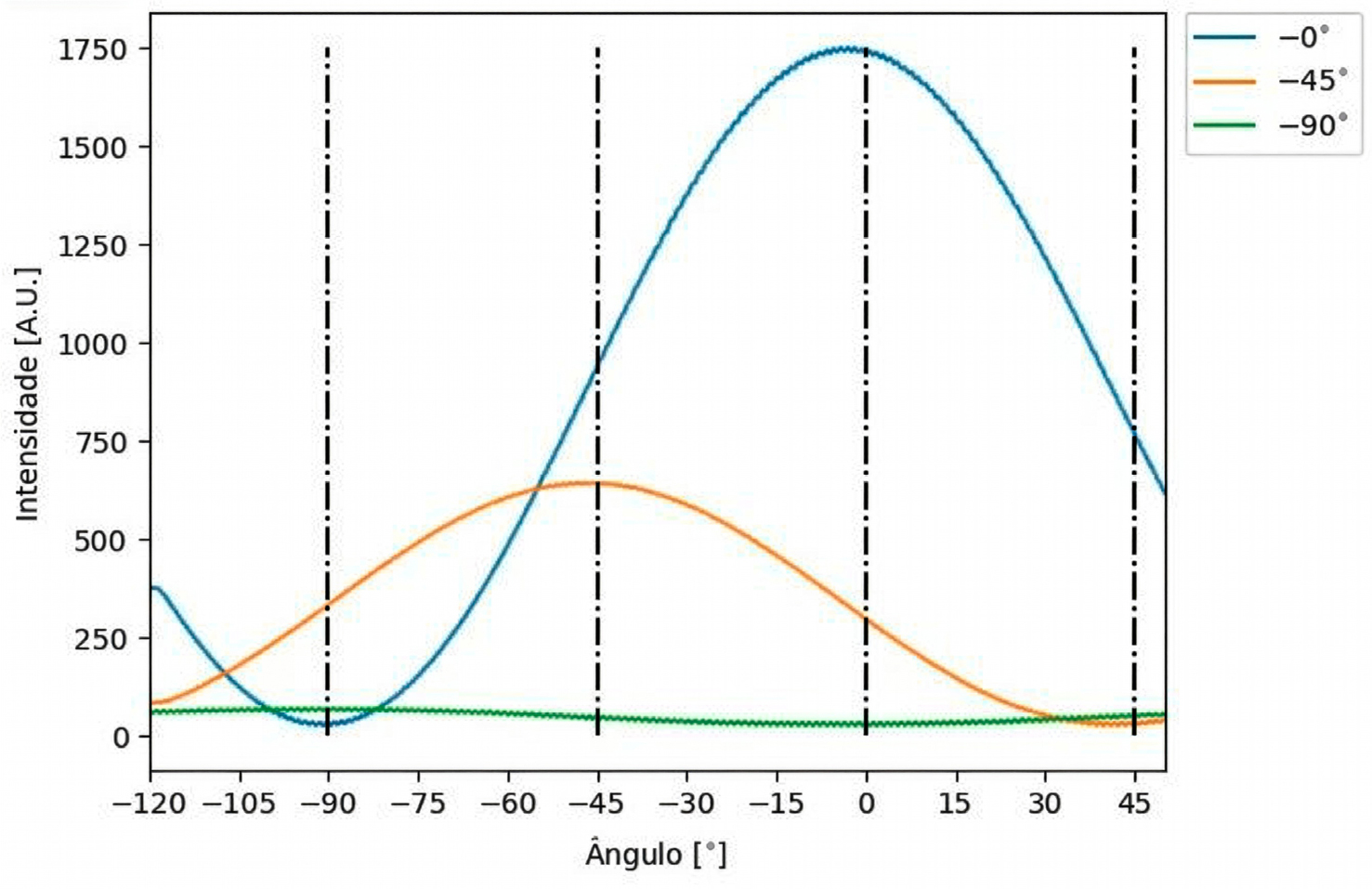
Feita a correção dos erros pela remoção do offset médio (~30), o máximo da luz transmitida com o segundo polarizador a -45° é de 598 e a -90° de 306, cerca de 50% como esperado e isto apesar do último polarizador fazer 90° com o primeiro. Apesar da projeção do campo segundo o eixo ser de \(1/\sqrt{2}=\cos\)(45°), a potência coletada depende do seu quadrado e portanto deveria ser de 50%. Notamos que o máximo da curva amarela é quando o terceiro polarizador se alinha com o segundo que se encontra a -45°.

A curva a azul desvia-se significativamente da lei de Malus mas tal deve-se provavelmente ao sensor de luz (BPW34), uma vez que a sua eficiência de conversão fotoeléctrica (capacidade de resposta) depende da potência óptica incidente.

A descrição quântica.

O princípio de sobreposição, formulado primeiramente por Dirac, é uma forma de dizer que, para prever as correlações observadas no mundo quântico, nós precisamos de todos os vetores que descrevem o espaço de situações fisicamente possíveis, os observáveis, e a sobreposição desses vetores também corresponde a uma solução para dois ou mais estados quânticos.

Vamos descrever o estado de polarização da luz como um vetor bi-dimensional, tal como ilustrado na FIGURA 3. Luz polarizada verticalmente corresponde a um vetor a apontar para cima \((0,1)\), e se for horizontal corresponde a \((1,0)\). Usamos a notação de Dirac para representar estes vetores, \(\left | V\right >\) e \(\left | H\right >\) respectivamente. Um vetor arbitrário escreve-se

\(|\alpha\rangle=\cos\left.\alpha|V\right\rangle+\sin\left.\alpha| H\rangle\right.\)

A mecânica quântica explica como calcular: 1) a probabilidade de transmissão destes estados através de um polarizador, e 2) o estado à saída do polarizador. Aquando da passagem do estado \(\left | V\right >\) pelo segundo polarizador, orientado a 45°, temos que:

1. A probabilidade de transmissão é dada por

\(\mathrm{Prob}=|\langle V|P(45^\circ)\mid V\rangle|^2=\frac{1}{2}\)

onde \(P(45°)=\left|45°\right\rangle\left\langle45°\right|\).

2. O estado à saída é o estado orientado a 45°, ou seja, \(\alpha0\)45°. Em linguagem mais formal, diz-se que a medição projeta o estado quântico para o estado alinhado 45°,

\(\left|45°\right\rangle=1\left(\left|V\right\rangle+\left|H\right\rangle\right)/\sqrt{2}\)

Podemos continuar o exercício calculando a probabilidade de transmissão através do filtro final, orientado a \(\theta_2 =\) 90°, ou seja, correspondendo a um estado \(\left| H\right\rangle\). Esta é dada por,

\(\textrm{Prob}=\cos^2(45^{\circ}-\theta_2)\)

Neste caso particular, as regras da mecânica quântica explicam exatamente o comportamento observado na experiência. No entanto poder-se-ia generalizar esta interpretação a qualquer ângulo, e fazendo a relação entre a soma de todos os fotões que atravessam o sistema e os iniciais, concluiriamos ser essa relação sempre igual à relação das intensidades luminosas à entrada e à saída do sistema.

Num artigo complementar a este (versãoteórica), oferecemos uma explicação mais detalhada da experiência de Malus, em termos dos fenómenos quânticos microscópicos. Tentamos oferecer uma visão mecânica do comportamento das partículas uma a uma, usando o conceito de variáveis escondidas.