A ideia de usar sistemas quânticos para fazer computação surgiu mais de uma década antes do trabalho inovador de Shor. Já na década de 80, os cientistas antecipavam o potencial da física quântica para resolver problemas importantes e complexos. Um dos principais problemas com que os físicos estavam familiarizados era o cálculo da solução das equações da mecânica quântica. A mecânica quântica é a teoria que descreve a natureza em escalas muito pequenas e explica como as partículas fundamentais se comportam e interagem entre si para formar moléculas e materiais. O problema é que as leis da mecânica quântica são altamente contraintuitivas e permitem que uma dada partícula, como um eletrão, esteja em muitos estados ao mesmo tempo, naquilo que se designa por estado de sobreposição quântica. Se considerarmos um caso simplificado em que uma dada partícula pode estar em duas posições, então um conjunto de n dessas partículas pode, em princípio, estar numa sobreposição de 2^n estados. Para 50 partículas, isto já resultaria em mais de um quatrilhão de possibilidades coexistentes. Este crescimento exponencial da complexidade é a principal razão pela qual a previsão do comportamento da matéria à escala quântica é extremamente desafiante. Perante este problema, o famoso físico Richard Feynman teve a seguinte ideia: sugeriu que, para simular o comportamento de sistemas quânticos, o próprio computador deveria obedecer as leis da mecânica quântica e ser capaz de criar e manipular essas sobreposições.

Esta ideia revelou-se bastante frutífera. Desde a proposta de Feynman e o algoritmo inovador de Shor, os investigadores desenvolveram muitos algoritmos quânticos, isto é, algoritmos que só podem ser executados num computador quântico. Estes algoritmos têm o potencial de serem aplicados não só para melhorar a nossa compreensão fundamental da natureza a nível quântico, mas também para resolver de forma mais eficiente muitos problemas práticos relacionados com o desenvolvimento de novos materiais, medicamentos ou fertilizantes, bem como problemas complexos de otimização relevantes para a indústria. Contudo, para explorar essas possíveis vantagens computacionais, uma tarefa de engenharia formidável se apresenta: a construção de um computador quântico de grande escala.


Criar e controlar bits quânticos.

Os computadores que utilizamos no nosso dia-a-dia processam informação codificada em bits clássicos, que abstratamente são representados por dois estados: “0” ou “1”. A representação física destes 0s e 1s tomou várias formas ao longo do tempo. Nos primeiros computadores da primeira metade do século 20, um bit era codificado como a presença ou ausência de um orifício num cartão de papel (chamado cartão perfurado), enquanto nos discos rígidos modernos são áreas minúsculas de um disco de metal que são magnetizadas ou desmagnetizadas. Uma computação clássica pode ser vista como uma manipulação destes 0s e 1s, utilizando portas lógicas, para calcular o resultado de um determinado problema.

Já num computador quântico, a unidade básica de informação é o bit quântico, ou quibit, que pode estar numa sobreposição quântica de dois estados, “0” e “1” (FIGURA 1).


FIGURA 1. bits vs. qubits, a) Um bit clássico pode tomar um de dois valores, “0” ou “1”, b) Um conjunto de n bits pode estar numa de \(2^n\) configurações possíveis, c) Um bit quântico, ou quibit, pode estar numa superposição quântica de dois estados, que denotamos com a notação “braket” como “\(\left | 0\right >\)” e “\(\left | 1\right >\)”. Os coeficientes \(\alpha\) e \(\beta\) dão-nos a probabilidade \(P_0\) de encontrarmos o estado “\(\left | 0\right >\)” e \(P_1\) de encontrarmos o estado “\(\left | 1\right >\)”, respetivamente, d) Um conjunto de n quibits pode estar numa superposição de até \(2^n\) configurações possíveis.

Para realizar uma computação quântica, os bits quânticos são manipulados através de portas quânticas, seguindo a prescrição fornecida por um algoritmo quântico. Estas portas podem alterar o estado de sobreposição de cada quibit individualmente, mas também acoplar diferentes qubits para criar estados entrelaçados (FIGURA 2).


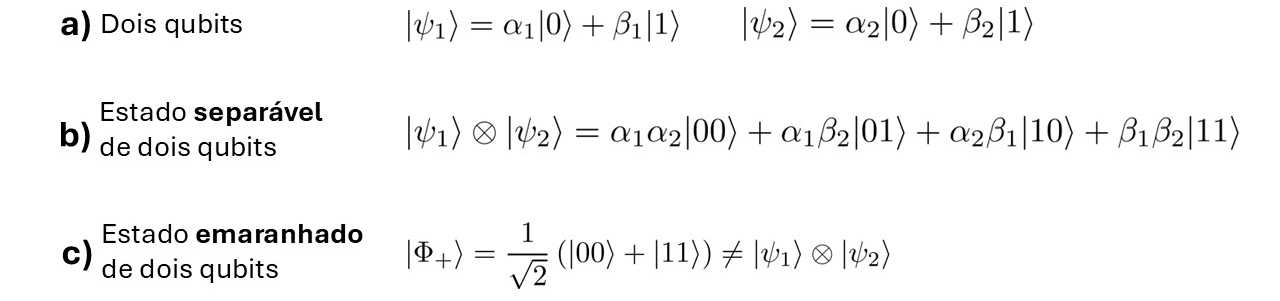
FIGURA 2. Emaranhamento quântico, a) Dois quibits estão cada um numa dada superposição de dois estados “\(\left | 0\right >\)” e “\(\left | 1\right >\)”, b) Quando dois quibits estão num estado quântico separável, o seu estado conjunto pode ser escrito como um “produto” dos seus estados individuais, c) Quando dois quibits estão num estado quântico emaranhado, o seu estado conjunto não pode ser escrito como um produto dos seus estados individuais.

Para dar um exemplo, o estado entrelaçado mais simples de dois quibits é o estado de sobreposição de “00” e “11”, ou seja, dos dois quibits no estado “0” e os dois quibits no estado “1”. Mas estas sobreposições podem tornar-se muito complexas e conter um número exponencialmente maior de possibilidades, como discutimos acima. Significa isto que um computador quântico pode ser sempre exponencialmente mais rápido que um computador clássico? Infelizmente, não. O problema é que as leis da mecânica quântica afirmam que, ao medir um estado de sobreposição de bits quânticos para determinar a sua configuração, apenas se observa uma das muitas possibilidades, com uma dada probabilidade. Portanto, não há forma de aceder diretamente a todas estas possibilidades exponencialmente numerosas ao mesmo tempo. O desafio de desenvolver algoritmos quânticos consiste, então, em utilizar inteligentemente as portas quânticas para amplificar a probabilidade da resposta correta para um determinado problema computacional.

Em relação ao hardware, ou seja, os elementos físicos que serão usados para construir o computador quântico, existem diversas propostas que foram desenvolvidas ao longo das últimas décadas. Uma das mais conhecidas é a chamada armadilha de iões, onde iões individuais levitam em posições fixas por ação de um campo magnético. Neste caso, cada quibit corresponde ao spin de cada ião e as portas quânticas são realizadas por impulsos laser que incidem sobre os iões. Outra proposta é utilizar partículas individuais de luz, ou fotões, que podem viajar numa sobreposição de diferentes trajetórias e, assim, codificar quibits (FIGURA 3).


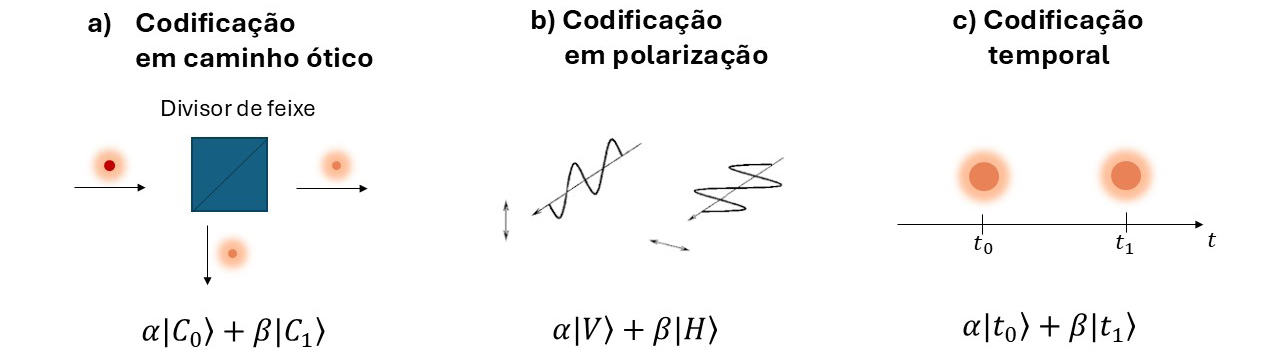
FIGURA 3. Qubits podem ser codificados usando diferentes propriedades dos fotões (partículas de luz), a) Um divisor de feixe coloca um fotão que nele impinge numa superposição de dois caminhos óticos possíveis \(C_0\) e \(C_1\), b) Fotões podem estar numa superposição de dois estados de polarização (ou direção de oscilação do campo eletromagnético) ortogonais, por exemplo, polarização vertical \(V\) e horizontal \(H\), c) Um quibit também pode ser codificado em dois tempos de chegada diferentes \(t_0\) e \(t_1\).

Mais uma possibilidade são os quibits supercondutores, constituídos por circuitos elétricos arrefecidos a temperaturas muito baixas de modo a se comportarem como supercondutores, resultando disso que as correntes e tensões elétricas se comportam de forma quântica.

Independentemente da tecnologia utilizada, o principal desafio para a construção de um computador quântico em larga escala reside na extrema sensibilidade dos estados de sobreposição à decoerência. A decoerência é a razão pela qual não experienciamos as peculiaridades da mecânica quântica no nosso quotidiano. A interação de um estado quântico com o ambiente que o rodeia tende a destruir as sobreposições (ou coerência quântica) e a transformar o estado quântico num estado clássico mais familiar, em que um objeto se encontra num estado A ou B, em vez de uma sobreposição de A e B. Por isso, para manter as sobreposições quânticas e explorá-las para computação, os quibits precisam de estar muito bem isolados. No entanto, não podem ser completamente isolados, dado que, para criar e manipular essas sobreposições complexas, é necessário acoplar os quibits entre si para implementar as portas quânticas. Nestas exigências aparentemente contraditórias, que requerem tanto o acoplamento fraco como o forte dos quibits, está assente a principal dificuldade de criar um computador quântico em larga escala.

A esperança de que este enorme desafio possa vir a ser superado encontra-se na teoria da correção de erros quânticos, para a qual Peter Shor também contribuiu com trabalhos muito importantes na década de 90. Esta teoria explica como corrigir os erros que surgem numa computação quântica devido à decoerência e às portas quânticas imperfeitas. No entanto, a implementação destes protocolos de correção de erros é dispendiosa. Por cada quibit que desejamos utilizar na nossa computação quântica, precisamos de muitos mais para realizar a correção quântica de erros – um fator que pode ser até mil vezes maior. Portanto, um computador quântico capaz de realizar correção de erros e ainda assim lidar com problemas complexos poderá exigir milhões de quibits. O caminho para construir um dispositivo deste tipo será longo e árduo, mas, entretanto, os investigadores já conseguem demonstrar feitos notáveis e superar até os melhores supercomputadores em determinadas tarefas específicas.


“Vantagem quântica” em dispositivos quânticos de pequena-escala.

Claramente, o primeiro objetivo na construção de um computador quântico é demonstrar a capacidade de controlar um pequeno número de bits quânticos e aplicar portas quânticas. Isto já foi conseguido em inúmeras experiências de prova de conceito em universidades e laboratórios de todo o mundo, utilizando muitas das formas possíveis de construir um computador quântico (iões, fotões, supercondutores…). Nos últimos anos, o investimento público e privado na investigação em computação quântica aumentou consideravelmente, especialmente desde que gigantes tecnológicos como a Google, a IBM, a Intel e a Microsoft entraram na área. Este investimento possibilitou a conquista de objetivos mais ambiciosos do que simplesmente manipular alguns quibits.

Um marco importante que tem sido um dos principais focos de investigação em computação quântica na última década é o seguinte: qual é a tarefa mais simples que podemos realizar com um dispositivo quântico de pequena escala de forma muito mais rápida do que com os nossos métodos convencionais de computação? Há dois pontos importantes que devem ser aqui enfatizados. Em primeiro lugar, a tarefa em questão não tem necessariamente de ser útil em termos práticos; o objetivo é apenas demonstrar que uma grande aceleração computacional é possível devido à mecânica quântica. Em segundo lugar, idealmente seria possível realizá-la com um dispositivo quântico de pequena escala, que seria ruidoso por não possuir quibits e recursos suficientes para realizar a correção de erros quânticos. Tal objetivo tem sido denominado na área como o de alcançar a vantagem computacional quântica.

Em 2019, a equipa de computação quântica da Google, liderada por John Martinis, foi a primeira a afirmar ter alcançado este objetivo, utilizando um chip com 53 quibits supercondutores1, 2. Em dezembro de 2020, a equipa de Jian-Wei Pan, da Universidade de Ciência e Tecnologia da China, também afirmou ter alcançado tal objetivo, desta vez com um aparato experimental capaz de criar, manipular e detetar fotões3, 4. Mas que tarefa executam estes dispositivos e porque é que ela é difícil para os computadores clássicos? Esta tarefa é designada de “problema de amostragem”, e o objetivo é gerar números aleatórios, onde cada número aparece com uma determinada probabilidade. De certa forma, esta é uma tarefa natural se tivermos acesso a um estado quântico de muitas partículas. Como referido anteriormente, quando medimos um estado de sobreposição quântica, apenas uma entre um número exponencialmente grande de possibilidades é observada. Verificou-se que calcular as probabilidades de obter um determinado resultado da observação é uma tarefa muito difícil, cujo tempo aumenta exponencialmente com o tamanho do sistema quântico, mesmo utilizando os melhores algoritmos clássicos que conhecemos. Em 2010, Scott Aaronson e Alex Arkhipov, dois matemáticos do MIT, utilizaram este facto para demonstrar que um dispositivo quântico específico, denominado “amostrador de bosões” (boson sampler em inglês), podia gerar números aleatórios a partir de uma determinada distribuição de probabilidade muito mais rapidamente do que os computadores clássicos. Um bosão é um tipo de partícula fundamental, do qual são exemplo os fotões2. Um amostrador de bosões é um dispositivo capaz de gerar muitos fotões individuais, fazê-los interferir uns com os outros de forma aleatória e medir a posição final de cada um (FIGURA 4).


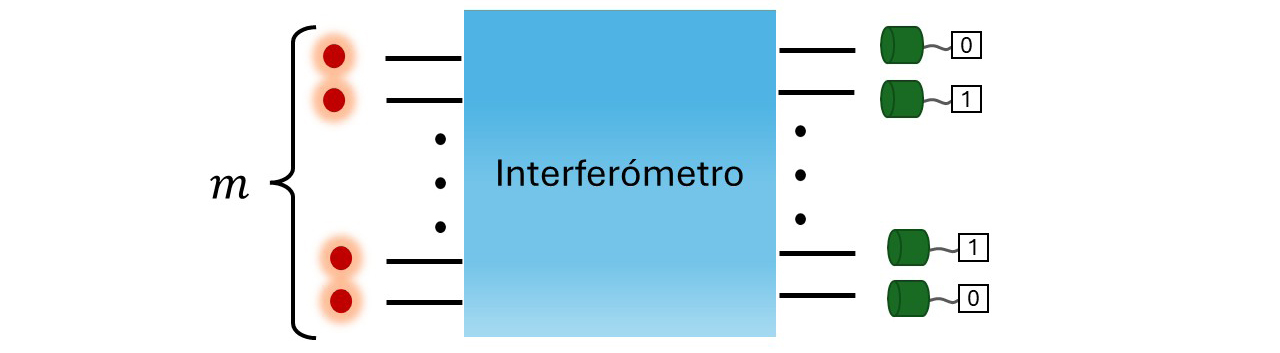
FIGURA 4. Amostrador de bosões. Fotões individuais são enviados em caminhos óticos até um interferómetro, um dispositivo composto de vários componentes óticos que fazem os fotões interferir aleatoriamente. À saída do interferómetro, detetores de fotões permitem-nos medir a distribuição final dos fotões nos \(m\) caminhos. Cada configuração final ocorre com uma certa probabilidade que depende do interferómetro, e determinar exatamente ou mesmo apenas estimar essa probabilidade para um número elevado de fotões e caminhos óticos é um problema computacionalmente complexo para um computador clássico.

A configuração final dos fotões fornece-nos um número aleatório de acordo com uma distribuição de probabilidade muito complexa. Uma contribuição crucial do trabalho de Aaronson e Arkhipov foi fornecer fortes evidências matemáticas de que, mesmo que este dispositivo seja afetado por certos erros experimentais, que são sempre inevitáveis, deveria ainda resolver um problema complexo de amostragem muito mais rapidamente do que qualquer computador clássico. O seu trabalho também lançou as bases matemáticas para o estudo da complexidade de outros problemas de amostragem que podem ser solucionados por computadores quânticos. De facto, logo após a proposta de amostragem de bosões, vários investigadores demonstraram que outras tarefas de amostragem complexas podem ser resolvidas por computadores quânticos mais convencionais, aplicando portas quânticas aleatórias e medindo o estado final.

Esta investigação levou à experiência realizada pelo grupo de computação quântica da Google em 2019, que resolve uma tarefa de amostragem muito complexa utilizando 53 quibits. Embora o seu dispositivo esteja longe da perfeição e sofra de importantes efeitos de decoerência, o seu trabalho demonstra que os efeitos quânticos desempenham um papel importante e que o dispositivo explora uma sobreposição de 2^53 (aproximadamente 9 quatrilhões!) de possibilidades. No seu trabalho original, a Google estimou que um supercomputador clássico precisaria de 10.000 anos para realizar a tarefa que o dispositivo da Google realiza em poucos minutos. Investigadores da IBM defenderam que, utilizando um método de simulação diferente, a mesma tarefa poderia ser resolvida em 2,5 dias5 pelo maior supercomputador do mundo. Ainda assim, o dispositivo da Google parece altamente vantajoso, tendo em conta o tempo e a energia necessários para manter o maior supercomputador do mundo a funcionar durante este período. Além disso, mesmo um aumento modesto no número de quibits no chip supercondutor da Google tornaria a simulação clássica impraticável, devido ao crescimento exponencial do custo computacional. Já a experiência realizada na China em 2020 baseia-se na proposta de amostragem de bosões de Aaronson e Arkhipov. Nesta experiência, foram detetados até 76 fotões

após passarem por um interferómetro que combina 100 trajetórias óticas, gerando mais de 10^30 possibilidades (1 milhão de quatrilhões!). Entretanto, a empresa Xanadu no Canadá conseguiu superar estes números impressionantes, aumentando significativamente o número de fotões e possibilidades envolvidas6. Acredita-se que estas últimas experiências são impossíveis de simular com computadores clássicos, mesmo utilizando o maior supercomputador do mundo. Contudo, só o tempo dirá se será realmente esse o caso. Pode acontecer que, no futuro, sejam encontrados algoritmos clássicos mais rápidos que consigam imitar o comportamento do dispositivo da Google ou da experiência chinesa ou canadiana, explorando, por exemplo, as imperfeições destes dispositivos.

Alcançar a vantagem quântica não é, portanto, um objetivo claramente definido que possa ser atingido de forma inequívoca. Deve ser visto como uma corrida entre a nossa forma padrão de computação, que também melhora rapidamente através da miniaturização e de novas descobertas em algoritmos clássicos, e um novo paradigma para a computação, que ainda está no início, mas que progrediu de forma impressionante nos últimos anos. Os investigadores em computação quântica acreditam geralmente que, a longo prazo, os computadores quânticos irão superar os clássicos, pelo menos para alguns problemas específicos, mas suficientemente importantes. O que é indiscutível é que os campos de investigação da computação clássica e quântica estão a aprender muito ao participar nesta corrida, e, por isso, o grande vencedor é a própria ciência.


De amostragem de bosões para computadores quânticos fotónicos.

A experiência chinesa de amostragem de bosões é, sem dúvida, um feito tecnológico impressionante: experiências óticas desta dimensão requerem a sincronização de dezenas de fotões, emitidos por uma ou várias fontes de fotões que devem ser de elevada qualidade e controladas com precisão, de modo a emitirem fotões idênticos entre si. De facto, a indistinguibilidade entre fotões é um fator necessário para se observarem determinados efeitos quânticos. Estes fotões têm depois de ser redirecionados por redes complicadas de fibras óticas, e manipulados por componentes óticos o mais transparentes possível. Finalmente, para se ler o resultado da computação, os fotões devem ser detetados por múltiplos fotodetetores, que devem ter uma eficiência elevada de modo a nenhuma informação se perder. Com equipamento e técnicas experimentais de alto nível, esta experiência foi capaz de enviar mais de setenta fotões em cem trajetórias óticas diferentes, gerando sobreposições quânticas ordens de grandeza superiores às da experiência de 53 quibits da Google.

No entanto, é importante realçar que um dispositivo capaz de realizar amostragem de bosões não é capaz de realizar qualquer computação quântica possível. Enquanto o dispositivo da Google pode ser considerado um computador quântico universal, no sentido em que tem qubits bem definidos e é capaz de executar todas as portas quânticas necessárias para a computação quântica, um amostrador de bosões deve antes ser visto como um modelo diferente e mais restrito de um computador quântico. Ainda assim, trata-se de um importante avanço tecnológico na construção de um computador quântico fotónico.

Existem alguns desafios experimentais característicos que se apresentam quando tentamos construir um computador quântico fotónico universal. Primeiramente, fotões podem ser facilmente absorvidos ou difundidos ao atravessarem fibras óticas ou os componentes óticos usados para os controlar, e ao se perderem, perde-se a informação que carregavam. Adicionalmente, fotões viajam à velocidade da luz, e isto torna-os difícil de controlar e preservar por muito tempo antes que sejam perdidos. Como mencionamos anteriormente, a fabricação de fontes fotónicas ideais que emitam fotões perfeitamente idênticos é um importante desafio técnico. Finalmente, certas portas quânticas requerem interações entre quibits. Algo parecido também acontece na computação clássica, por exemplo, com portas “Controlled-Not”, em que o estado de um bit alvo é negado (passando de “0” para “1”, ou de “1” para “0”), se e só se o estado de um segundo bit de controlo for “1”. Para aplicar a versão quântica desta porta em dois fotões, é necessário que estes interajam um com o outro, o que é muito difícil de se realizar na prática.

Apesar disso, as plataformas fotónicas também apresentam várias vantagens quando comparadas com outros sistemas físicos. Ao contrário de plataformas como circuitos supercondutores, que operam a temperaturas criogénicas, computadores fotónicos podem ser maioritariamente operados à temperatura ambiente (exceto, eventualmente, ao nível das fontes de fotões e fotodetetores), evitando a necessidade de sistemas de arrefecimento delicados e facilitando o seu escalonamento para sistemas maiores. Além disso, a mesma propriedade que dificulta a interação entre fotões também os torna muito robustos ao ruído ambiente e à decoerência. Fotões conseguem, portanto, atravessar rapidamente longas distâncias sem que a informação que transportam seja deteriorada, tornando-os uma excelente opção para transmitir informação quântica a longas distâncias. Sendo assim, é provável que qualquer plataforma para computação quântica, ainda que baseada primariamente noutros sistemas físicos que não os fotões, venha a utilizar quibits fotónicos para estabelecer comunicação entre outros quibits estacionários, como átomos ou spins eletrónicos.

Vários laboratórios, universidades e empresas estão a direcionar esforços, tanto teóricos como experimentais, para superar os diferentes desafios associados a construir computadores quânticos fotónicos com crescente número de quibits e portas quânticas. A empresa norte- americana PsiQuantum demonstrou em 20247 conseguir fabricar com elevada qualidade vários dos componentes necessários para gerar, manipular, redirecionar e detetar fotões, e tem-se focado num modelo promissor para computação quântica fotónica que supera alguns dos obstáculos associados à perda de fotões e à dificuldade de os fazer interagir. Outro exemplo é a startup francesa Quandela, que tem vindo a desenvolver várias gerações de processadores quânticos fotónicos com crescente dimensão8, e propôs recentemente um modelo alternativo de computação que combina quibits fotónicos com quibits em spins, combinando as vantagens dos dois tipos de sistemas9, 10. Aqui em Portugal, no Laboratório Internacional Ibérico de Nanotecnologia, estudam-se métodos teóricos para validar o correto funcionamento deste tipo de processadores, que serão essenciais quando estes começarem a atingir dimensões grandes o suficiente para que um computador clássico não consiga simular, e portanto, verificar o seu comportamento.


A busca pelo computador quântico universal.

Na secção anterior vimos, com o exemplo da computação quântica fotónica, que cada plataforma física que escolhemos para codificar quibits (fotões, iões, spins…) apresenta vantagens características, mas também dificuldades experimentais. Além disso, sistemas quânticos são sensíveis ao ambiente, e por isso, a informação quântica codificada em quibits é frágil e suscetível a erros, especialmente quando comparada à informação clássica manipulada pelos computadores tradicionais, que é quase perfeitamente preservada. Assim, para realizar computação quântica, é impreterível desenvolver algoritmos para deteção e correção de erros. Estes algoritmos tipicamente envolvem a codificação redundante de cada quibit em múltiplos sistemas físicos, por exemplo, repetindo o estado de um quibit em 100 ou 1000 fotões. Isso significa que, para construir um computador quântico universal que funcione apesar do ruído ambiente, é necessário ser capaz de gerar e manipular milhões de quibits com elevada precisão e rapidez, o que impõe requisitos rigorosos a nível dos recursos, controlo, processamento e consumo energético necessários para rodar um computador quântico.

Vemos, portanto, como a construção de um computador quântico de larga-escala tolerante a erros se figura um exigente desafio experimental. Apesar disso, progressos têm sido alcançados a largos passos nas últimas décadas, em diversas frentes. Recentemente, um entusiasmante resultado pela equipa da Google demonstrou que o seu processador quântico baseado em circuitos supercondutores é tolerante a erros quando operado sob um algoritmo de deteção e correção de erros11. Esta foi a primeira vez que se verificou este comportamento num processador quântico, representando um novo patamar atingido na busca por um computador quântico universal.

Computadores quânticos representam uma tecnologia altamente promissora, com potencial utilidade prática transversal a várias indústrias e áreas do conhecimento, desde a química e as ciências de materiais a problemas de otimização em logística e finanças. Contudo, o seu desenvolvimento experimental ainda está na sua infância, e permanece em aberto se será possível superar todos os obstáculos, técnicos ou mesmo fundamentais, à construção de um computador quântico universal. O que é inquestionável é que a computação quântica introduziu um novo paradigma para a conceptualização e entendimento da codificação e processamento de informação, abrindo novos horizontes nas ciências da informação e computação. Questões fascinantes, como definir os limites entre a informação quântica e a clássica, e mapear os problemas em que a vantagem quântica é única, continuam em aberto, e a sua exploração trará, indubitavelmente, um conhecimento ainda mais profundo e completo sobre a natureza fundamental da informação. A corrida pelo computador quântico universal, travada em diferentes plataformas, continuará a fomentar a inovação de diferentes tecnologias para geração, manipulação e deteção de sistemas quânticos, com aplicações em metrologia, telecomunicações, criptografia e outros ramos da ciência. Assim, a computação quântica já está a redefinir as fronteiras da ciência e tecnologia, e os esforços para a concretizar constituem uma frutífera aposta no seu inegável potencial transformador.