1. O que são Paradoxos?

Paradoxos são afirmações que levam a uma contradição lógica, ou a situações que desafiam a intuição ou o senso comum. Existem diferentes tipos de paradoxos: os paradoxos lógicos, que revelam falhas ou inconsistências em sistemas lógicos ou matemáticos; os paradoxos semânticos, que surgem devido a ambiguidades na linguagem; e os paradoxos físicos, que desafiam a nossa compreensão do mundo físico e podem levar a novas teorias. O paradoxo dos gêmeos, na relatividade restrita, é um exemplo.

Eis um exemplo de paradoxo semântico — o paradoxo do mentiroso:

\(F\) = ”Esta frase é falsa.”

Se \(F\) for verdadeira, então é falsa. Se \(F\) for falsa, então é verdadeira. Isto contradiz a lógica clássica, porque uma frase não pode ser simultaneamente verdadeira e falsa.

Os paradoxos são importantes na filosofia, na lógica e na ciência, porque nos forçam a examinar as nossas hipóteses e a refinar os nossos conceitos e fundamentos. A resolução de um paradoxo pode levar a uma nova compreensão e a avanços significativos. Os paradoxos são, pois, desafios ao nosso pensamento crítico. Passemos então à discussão de alguns dos mais intrigantes.

O Paradoxo da Lâmpada de Thomson.

Um dos paradoxos mais interessantes foi proposto por James Thomson (1922–1984), um filósofo britânico que trabalhou em áreas como a filosofia da mente, a ética e a filosofia da matemática. Chama-se o paradoxo da lâmpada de Thomson, em homenagem ao seu criador, e está incluído num artigo intitulado “Tasks and Super-Tasks”, publicado por ele em 1954 na revista Analysis.

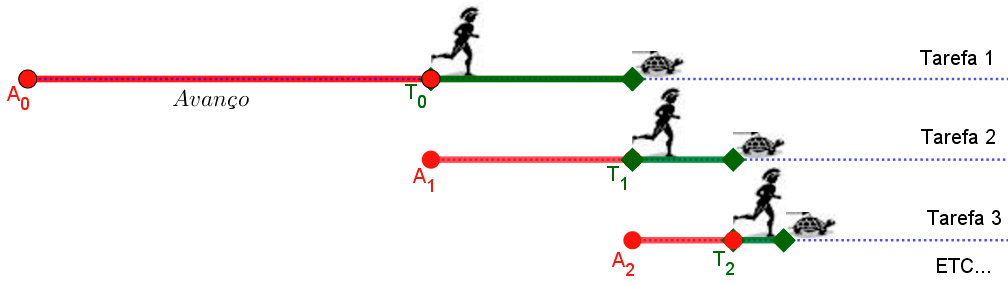
A lâmpada de Thomson é um paradoxo que envolve uma super-tarefa, isto é, um processo que consiste numa infinidade de tarefas. Na lâmpada de Thomson, as tarefas são as seguintes:

1. Acendemos a lâmpada e mantêmo-la acesa durante 20 s (tarefa 0).

2. Depois apagamos a lâmpada, e mantêmo-la apagada durante 20/2¹ = 10 s (tarefa 1) (metade do tempo anterior).

3. Depois é acesa novamente, e mantida acesa durante 20/2² = 5 s (tarefa 2) (metade do tempo anterior), e assim sucessivamente.

A super-tarefa continua, com intervalos de tempo cada vez menores (cada um é metade do anterior). O processo de apagar e acender alternadamente a lâmpada pode continuar indefinidamente, mas dura um tempo finito igual a:

\(T=20+10+5+2,5+1,25+\cdots=\) 40 segundos

como veremos adiante. Isto é, apesar de termos uma infinidade de tarefas para executar (uma super-tarefa), o processo termina ao fim de 40 segundos!

Pergunta:

A lâmpada estará acesa ou apagada após a conclusão deste processo infinito?

Esta pergunta é, no mínimo, desconcertante e não tem uma resposta óbvia (se é que tem resposta!).

Duração da super-tarefa.

Vamos agora ver que, de facto, matematicamente, o processo total demora apenas 40 segundos a completar, de acordo com a teoria de limites, criada por Augustin-Louis Cauchy (1789–1857), que já faz parte dos currículos de ensino secundário.

• Qual a duração, \(S_n\), das primeiras \(n\) tarefas? É igual a:

\(S_n=20\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^{n-1}}\right)\) segundos

que é uma soma do tipo:

\(S_n=A\cdot\left(1+{\color{Red} r+r^2+\cdots+r^{n-2}+r^{n-1}}\right)\)

com \(A=20\) e \(r=1/2\).

• Multiplicando ambos os membros por r, obtemos

\(r\cdot S_n=A\cdot\left({\color{Red} r+r^2+r^3\cdots+r^{n-1}}+r^n\right)\)

• Subtraindo membro a membro essas duas últimas expressões, e supondo \(r\ineq 1\), obtemos:

\((1-r)\cdot S_n=A\cdot(1-r^n)\Longrightarrow S_n=A\cdot\frac{1-r^n}{1-r}\)

Cauchy formalizou o conceito de limite, o que permitiu lidar com sucessões e somas infinitas que convergem para um valor finito.

Recordemos (ver a FIGURA 1): “uma sucessão de números reais converge para um limite finito \(l\), se e só se, para todo \(\epsilon >0\), existe um \(n_o\in \mathbb{N}\) a partir do qual todos os termos dessa sucessão pertencem ao intervalo \([\ell-\epsilon,\ell+\epsilon]\)”.

Se aceitarmos que o tempo é contínuo (e, portanto, infinitamente divisível), então o processo tem uma duração finita igual a

\(\lim_{n\to\infty}S_{n}=A\lim_{n\to\infty}\frac{1-r^{n}}{1-r}=20\frac{1}{1-\frac{1}{2}}=\) 40 segundos

Já que \(\lim_{n\to\infty}r^{n}=0\), se \(0\)<\(r\)<\(1\). É, pois, possível realizar uma super-tarefa (isto é, um número infinito de tarefas) num tempo finito!

Mas a pergunta persiste: “A lâmpada estará acesa ou apagada após a conclusão deste processo infinito?” Não há resposta para esta pergunta. A conclusão é que a divisibilidade infinita do tempo cria dificuldades.

2. Paradoxos de Zenão de Eleia.

Mas regressemos a um tempo distante, de há cerca de 2500 anos atrás. Mais propriamente ao tempo de Zenão de Eleia que foi um Filósofo grego (490–430 a.C.?) da cidade de Eleia (hoje Vélia, no sul da Itália), discípulo de Parménides, cujas ideias defendia através de paradoxos. Os paradoxos de Zenão tornaram-se famosos, sobretudo pela divulgação feita por Aristóteles, e ainda hoje são discutidos no contexto dos fundamentos do tempo (e do espaço) contínuo e discreto. Os mais famosos são o paradoxo de Aquiles e a Tartaruga, o da Dicotomia, o da Flecha e outros.

O objetivo dos paradoxos era mostrar que a crença no movimento e na pluralidade leva a contradições lógicas. A sua relevância persiste na física e na matemática modernas, desafiando- nos a repensar conceitos fundamentais.

Paradoxo da Dicotomia.

Um corredor parte de 0 e quer chegar à meta \(M\), situada a uma distância \(d=\)100 metros de 0.

• Para chegar à meta, tem de percorrer primeiro metade do caminho (50 metros).
• Depois, metade da metade restante (mais 25 metros).
• E assim sucessivamente, infinitamente (ver a FIGURA 2).

Conclusão

O corredor nunca conseguirá chegar à meta!

Este paradoxo reforça a ideia de que a divisibilidade infinita do espaço pode levar a conclusões estranhas.

Qual é a distância total percorrida pelo corredor quando ele termina, após a infinidade de corridas parciais acima descritas (primeiro 50 m, depois 25 m, depois 12,5 m, etc.)? É igual a:

\(\frac{100}{2}+\frac{100}{2^2}+\frac{100}{2^3}+\cdots\)

\(=\frac{100}{2}\left ( 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots \right )\) (uma soma infinita!)

\(=\frac{100}{2}\cdot\frac{1}{1-\frac{1}{2}}=100\) (mais de 2000 anos depois!)

Se aceitarmos a divisibilidade infinita do espaço, ou se aceitarmos a noção de um espaço contínuo, então, do ponto de vista puramente matemático, o corredor pode e irá completar a corrida.

Exercício.

Se o corredor corre com uma velocidade \(V=\) 20 km/h, quanto tempo demora a corrida?

Aquiles e a Tartaruga: A Corrida Impossível?

Aquiles, conhecido pela sua velocidade, compete com uma tartaruga, a quem dá um avanço inicial.

Aquiles deve chegar primeiro ao ponto onde a tartaruga começou. No entanto, quando lá chega, a tartaruga já avançou um pouco. Este processo repete-se infinitamente (ver a figura abaixo), impedindo Aquiles de ultrapassar a tartaruga.

O que está em causa é a nossa intuição sobre o movimento contínuo e a possibilidade de percorrer um número infinito de distâncias (uma supertarefa) num tempo finito.

Exercício.

Supõe que: (i) a velocidade de Aquiles é \(V_A\)km/h; (ii) o avanço da tartaruga é \(a\) km; (iii) e que \(0\)<\(r\)<\(1\) é um multiplicador, de tal forma que a velocidade da tartaruga é \(VV_T=r\cdot V_A\)km/h.

Perguntas:

1. Qual a posição de Aquiles no instante \(t\)? E da tartaruga?

2. Qual o instante do encontro?

3. Qual a distância total percorrida por Aquiles? E pela tartaruga?

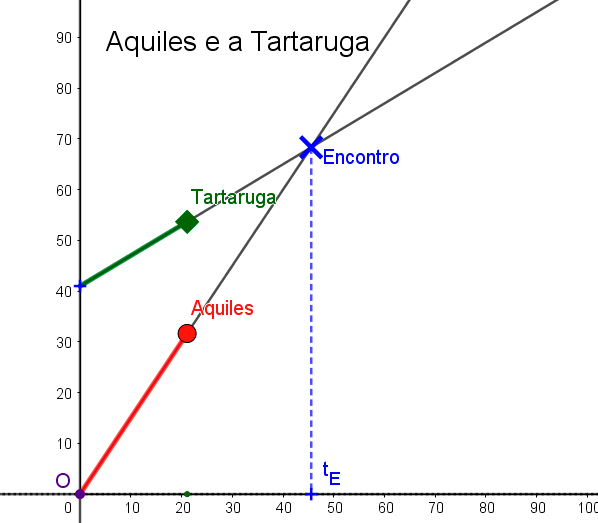
A geometria analítica, de Fermat e Descartes, permite calcular o instante de encontro \(t_E\), recorrendo a um diagrama de espaço-tempo (ver a FIGURA 3).

Mas assume os axiomas de Euclides:

• Uma reta é um contínuo de pontos, e
• Duas retas não paralelas intersectam-ne num único ponto.

Isto se aceitarmos a divisibilidade infinita do espaço e que é possível realizar um número infinito de tarefas num tempo finito!

Posição de Aristóteles.

Aristóteles (384–322 a.C.) foi um filósofo da Grécia Antiga. Ao lado de Platão, de quem foi discípulo na Academia, foi um dos pensadores mais influentes da história da civilização ocidental.

Aristóteles conhecia bem os paradoxos de Zenão e foi um dos seus principais divulgadores. Ao discuti-los, introduziu dois conceitos: o “infinito potencial” e o “infinito atual”. O que significam? Vejamos:

• O infinito potencial refere-se a um processo de crescimento ou de divisão que pode continuar indefinidamente, mas nunca é completado. É o infinito como uma possibilidade, não como uma totalidade. Exemplo: a divisão de uma linha em partes cada vez menores. Podemos continuar a dividir indefinidamente (a possibilidade), mas nunca chegaremos a um “ponto infinitesimal” final (a totalidade).
• O infinito atual refere-se a uma totalidade (o “fim” do processo infinito) que existe como um objeto completo e definido. É o infinito como uma entidade completa e não como um processo iterativo. Exemplo: o “ponto infinitesimal” final do exemplo anterior.

Aristóteles acreditava apenas no infinito potencial.

Exemplo: podemos construir os números naturais, começando com 1 e somando sucessivamente ao número anterior: \(1,1+1=2,2+1=3,3+1=4,\cdots\). Este é o infinito potencial, como possibilidade. Mas não existe a totalidade – algo a que possamos chamar o “fim” deste processo. Em linguagem moderna, não existe, segundo Aristóteles, algo a que possamos chamar o conjunto dos números naturais (a totalidade).

3. O que são Constantes Fundamentais?

Constantes Fundamentais são valores físicos numéricos que parecem ser universais e imutáveis. Não dependem de instrumentos ou medidas humanas arbitrárias. As que nos vão interessar são três: a constante de gravitação universal, \(G\), a velocidade da luz no vácuo, \(c\), e ainda a constante de Planck \(h\). As constantes fundamentais aparecem nas teorias mais essenciais da física, nomeadamente na Teoria da Relatividade e na Mecânica Quântica. A sua universalidade e imutabilidade conduzem a factos fascinantes. \(G\), \(c\), e \(h\) são pilares da nossa compreensão do universo.

Constante Gravitacional G.

Sir Isaac Newton (1642–1727) foi um matemático, físico, astrónomo, teólogo e autor inglês (descrito no seu tempo como um ”filósofo natural”), amplamente reconhecido como um dos cientistas mais influentes de todos os tempos e como uma figura-chave na Revolução Científica.

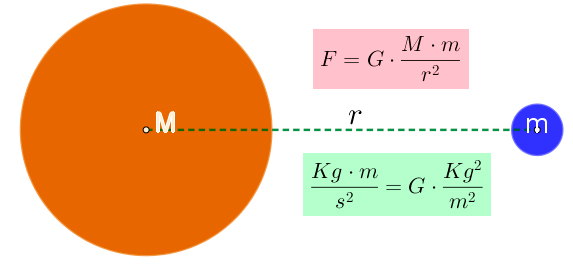
A constante gravitacional \(G\) está presente na lei da gravitação de Newton e na relatividade geral de Einstein (Universalidade). Não depende das propriedades dos objetos (Independência) e relaciona a curvatura do espaço-tempo com massa e energia (Geometria do Espaço-Tempo). Em unidades SI, é dada por:

\(G=\) 6,674184m³kg⁻¹s⁻²

Velocidade da Luz no Vácuo c.

Albert Einstein (1879–1955) desenvolveu a teoria da relatividade geral, um dos pilares da física moderna, ao lado da mecânica quântica. Embora seja mais conhecido por sua fórmula de equivalência massa-energia, \(E=mc^2\) — “a equação mais famosa do mundo” —, foi laureado com o Prémio Nobel de Física de 1921 “pelos seus contributos à física teórica” e, especialmente, por sua descoberta da lei do efeito fotoelétrico.

A velocidade da luz no vácuo , é considerada o limite para a propagação de objetos e de informação. É a mesma para todos os observadores (Invariância). Relaciona espaço e tempo na teoria da relatividade e é usada na equivalência entre massa e energia, \(E=mc^2\). Em unidades SI, é dada por

\(c=\) 299792458 m/s

Constante de Planck \(h\).

Max Planck (1858–1947) foi um notável físico alemão, considerado o pai da física quântica e um dos físicos mais importantes do século XX. Planck foi laureado com o Nobel de Física de 1918 pelas suas contribuições na área da física quântica.

A constante de Planck, \(h\), aparece na quantização da energia — a energia é emitida ou absorvida em quanta, \(E=h\nu\) — a energia \(E\) de um fóton proporcional à sua frequência, \(\nu\).

Aparece ainda na Dualidade Onda-Partícula, e no Princípio da Incerteza de Heisenberg, como veremos daqui a pouco. Em unidades SI, é dada por

\(h=\) 6,62607015 · 10⁻³⁴ J · s (Joules segundo)

4. O que são Unidades de Planck?

As unidades de Planck constituem um sistema de unidades “naturais”, derivado das constantes fundamentais: velocidade da luz (\(c\)), constante gravitacional (\(G\)) e constante de Planck reduzida (\(\hbar=h/2\pi\)). Embora, originalmente, o objetivo tenha sido encontrar unidades que simplificassem os cálculos, Planck tinha uma motivação extra: criar unidades independentes de medições humanas arbitrárias. Elas definem a escala onde a física quântica e a gravidade se tornam igualmente importantes e onde as teorias atuais podem falhar.

Max Planck derivou as unidades de Planck combinando \(G\), \(c\) e \(h\) para deduzir as seguintes unidades derivadas:

• Comprimento de Planck: \(l_{P}=\sqrt{\frac{\hbar G}{c^{3}}}\approx1.616\cdot10^{-35}\) metros
• Tempo de Planck: \(t_{P}=\sqrt{\frac{\hbar G}{c^{5}}}\approx5.391\cdot10^{-44}\) segundos
• Massa de Planck: \(m_{P}=\sqrt{\frac{\hbar c}{G}}\approx2.176\cdot10^{-8}\) kg

O significado das unidades de Planck é profundo: elas impõem limites para a física — indicam que as nossas teorias atuais são incompletas. Sugerem que a natureza do espaço e do tempo em escalas muito pequenas pode ser diferente do que imaginamos. Desafiam a nossa compreensão e inspiram a busca por uma nova física (Gravitação Quântica). Levantam questões sobre o que é mensurável, o que significa “real” e sobre os limites do conhecimento.

5. O Princípio da Incerteza de Heisenberg.

Existe um limite fundamental para a precisão com que podemos conhecer simultaneamente certos pares de propriedades físicas. Por exemplo, é impossível medir a posição e o momento (= massa · velocidade) de um objeto quântico (Heisenberg):

\(\Delta x\Delta p\geq\hbar/2\)

A medição de uma propriedade afeta a outra, revelando a natureza probabilística do mundo quântico. Portanto, para medir distâncias aproximadamente iguais a \(\approx l_P\) (comprimento de Planck), é necessário usar energias extremamente altas. Quanto menor for a distância que se quer “ver”, maior é a energia necessária (Incerteza e Localização). Mesmo com medições “perfeitas”, não poderíamos conhecer simultaneamente a posição e o momento com precisão arbitrária. É um limite da natureza, não apenas da tecnologia.

A altas energias, os efeitos gravitacionais tornam-se significativos. Concentrar muita energia num espaço tão pequeno quanto \(l_P\) criaria uma distorção tão grande no espaço-tempo (de acordo com a Relatividade Geral) que poderia formar-se um buraco negro. Este cenário implica que há um limite fundamental para a nossa capacidade de medir distâncias com precisão. Tentar medir uma distância menor que \(l_P\) exigiria tanta energia que criaria um buraco negro, tornando a medição impossível.

De novo a Lâmpada de Thomson.

O tempo de Planck (\(t_P\)) é considerado o menor intervalo de tempo significativo que pode ser medido e que faz sentido na física teórica atual: \(t_{P}\approx5,391\cdot10^{-44}\).

Qual o maior \(n\) tal que \(20/2^n\)s é maior do que o tempo de Planck \(t_P\)? Para esse \(n\), a lâmpada está acesa ou apagada?

Como \(t_{P}\approx5,391\cdot10^{-44}\)s, queremos encontrar o maior inteiro tal que

\(\frac{20}{2^n}>5.391\cdot10^{-44}\Longleftrightarrow\)

\(2^{n}<\frac{20}{5.391\cdot10^{-44}}\Longleftrightarrow\)

\(2^n\)<\(3.7099\times10^{44}\) (aproximadamente)

Agora, aplicamos o logaritmo de base 10 a ambos os lados:

\(\textrm{log}_{10}\left ( 2^n \right )<\textrm{log}_{10}\left ( 3.7099\times 10^{44} \right )\Leftrightarrow \)

\(n\cdot\textrm{log}_{10}\left ( 2 \right )<\textrm{log}_{10}\left ( 3.7099\right )+\textrm{log}_{10}\left ( 10^{44} \right )\Leftrightarrow \)

\(n\cdot\textrm{log}_{10}\left ( 2 \right )<\textrm{log}_{10}\left ( 3.7099\right )+44\)

Usamos os valores aproximados: \(\textrm{log}_{10}\left ( 2 \right )\approx 0,30103\) e \(\textrm{log}_{10}\left ( 3,7099 \right )\approx 0,5693\). Substituindo, obtemos:

\(n\cdot 0,30103\)<\(0,5693+44\Leftrightarrow \)

\(n\cdot 0,30103\)<\(44,5693\Leftrightarrow \)

\(n<\frac{44,5693}{0,30103}\Leftrightarrow \)

\(n\)<\(148,05\)

Como \(n\) deve ser um número inteiro e queremos o maior que satisfaça a desigualdade, o valor de \(n\) é 148.

Para esse \(n=\) 148, a lâmpada está acesa ou apagada?

O padrão da tarefa e o estado da lâmpada é o seguinte: se \(n\) é par, a lâmpada está acesa; se \(n\) é ímpar, a lâmpada está apagada. Como \(n=\) 148 é par, a lâmpada está acesa para essa tarefa.

Do ponto de vista físico, a resposta é conclusiva, já que é fisicamente impossível (com as nossas teorias atuais) medir ou sequer isolar um intervalo de tempo (ou comprimento) menor ou da ordem das unidades de Planck. A energia necessária para isso criaria uma perturbação tão violenta no espaço-tempo que a própria medição seria aniquilada pela formação de um buraco negro.

Isto implica que, para os paradoxos de Zenão, a “super-tarefa” de dividir o tempo ou o espaço infinitamente não pode ser fisicamente realizada ou observada além de um certo ponto. O universo impõe um limite fundamental à divisibilidade. Os paradoxos de Zenão, que surgem da assunção de divisibilidade infinita do espaço e do tempo, encontram um “obstáculo” físico nas escalas de Planck.

Não se trata de uma resolução filosófica completa da questão do infinito, mas sim de uma limitação física intransponível. Em suma, do ponto de vista da física, a impossibilidade de medição abaixo das escalas de Planck é, de facto, conclusiva no contexto das nossas teorias mais fundamentais (Mecânica Quântica e Relatividade Geral). Isso significa que, independentemente das soluções matemáticas para séries infinitas, o mundo físico tem uma “granularidade” fundamental que impede a realização da ideia de divisibilidade infinita de Zenão.

De novo o Paradoxo da Dicotomia.

O comprimento de Planck \(l_P\) é considerado o menor comprimento significativo que pode ser medido, ou que faz sentido na física teórica atual: \(l_P\approx\) 1,616×10⁻³⁵ metros.

No paradoxo de Zenão da dicotomia, o corredor tem que percorrer 100 metros no total. Para isso, ele percorre primeiro os primeiros 50 m (tarefa 1), depois os 25 m seguintes (tarefa 2), depois os 12,5 m seguintes (tarefa 3) e assim sucessivamente. Por isso, Zenão concluiu que a corrida não pode acabar, porque não se pode realizar uma super-tarefa (uma infinidade de tarefas) em tempo finito.

Claro que, segundo o cálculo infinitesimal de Cauchy e outros, a série dos comprimentos das sucessivas tarefas (percursos) tem uma soma finita igual a 100 m: \(50+25+12,5+\cdots=100\).

Embora matematicamente a divisão possa ser infinita, fisicamente há um limite — o comprimento de Planck (\(l_P\approx\) 1,6×10⁻³⁵ m). Para “medir” ou distinguir um intervalo de comprimento menor, ou da ordem de \(l_P\), o Princípio da Incerteza Posição-Momento (\(\Delta x\cdot \Delta p \geq \hbar/2\)) implica que a incerteza no momento (\(\Delta\)) e, consequentemente, na energia (\(\Delta E\)), teria de ser gigantesca.

Formalmente, \(\Delta x\) se se aproxima de \(l_P\), então: \(\Delta p \geq \frac{\hbar}{2l_P}\). Usando a relação energia-momento \(E\approx p\cdot c\) (para altas energias relativísticas), a energia associada seria:

\(\Delta E \approx \frac{\hbar c}{2l_P}\)

Substituindo \(l_P= \sqrt{\frac{\hbar G}{c^3}}\) virá:

\(\Delta E\approx\frac{\hbar c}{2\sqrt{\frac{\hbar G}{c^3}}}=\frac{\hbar c^2}{2\sqrt{\hbar G/c}}=\frac{1}{2}\sqrt{\frac{\hbar c^5}{G}}=\frac{1}{2}E_P\)

Ou seja, a energia necessária seria da ordem da Energia de Planck (\(E_p\)), que é uma quantidade colossal (\(\approx\) 1,22×10¹⁹ GeV).

Por outro lado, a Relatividade Geral indica que concentrar uma quantidade tão imensa de energia (ou massa, \(E/c^2\)) num espaço tão diminuto como \(l_P\), levaria à formação de um buraco negro. Se o “fim” da corrida envolvesse um segmento de comprimento inferior ao de Planck, qualquer tentativa de interagir com essa região para “detetar” o seu fim resultaria na criação de um buraco negro, que engoliria o evento. A corrida, nesse ponto, tornar-se-ia indetectável, no sentido em que a informação sobre o seu fim seria perdida para sempre.

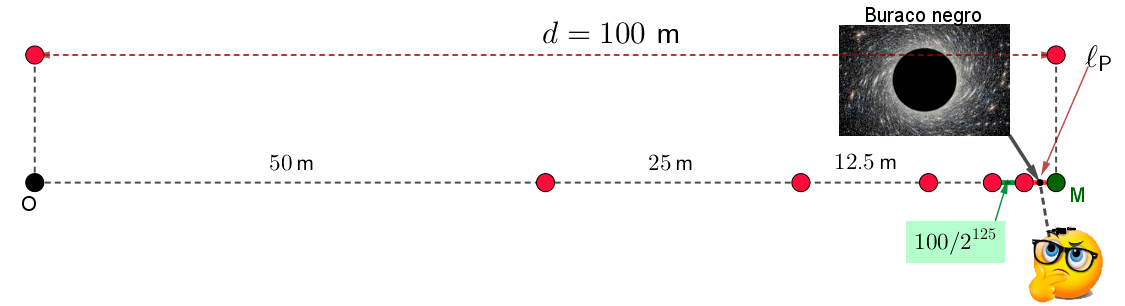
Isto não impede a corrida, mas impede a observação ou confirmação do seu fim, a nível fundamental!

O maior \(n\) tal que 100/2ⁿ m é maior do que o comprimento de Planck \(l_P\) é 122. Portanto, a última tarefa (percurso) a ser detectada é a tarefa 122, cujo comprimento é igual a 100/2¹²² m\(\approx\)1,88×10⁻³⁵ m.

Existe ainda outro aspecto que vale a pena considerar.

O paradoxo da dicotomia, ao exigir que o corredor percorra segmentos cada vez menores, implica que ele deve passar por “estados” sucessivos, a uma taxa cada vez mais rápida à medida que se aproxima da meta. Isto pode ser interpretado como um cenário onde há medições, ou “observações”, cada vez mais frequentes do progresso do corredor.

Se as interações que definem o “passar pelos pontos divisórios” das sucessivas tarefas: 50, 75, 87,5, \(\cdots\) pudessem ser modeladas como “medições” no sentido quântico, então a frequência crescente dessas “medições”, à medida que \(\Delta t\) se aproxima de \(t_p\left ( \Delta t\to t_p \right )\), poderia “congelar” a evolução do processo. O Princípio da Incerteza Energia-Tempo \(\left ( \Delta E\cdot \Delta t \geq \hbar/2 \right )\) torna isso ainda mais complexo, pois para ter um \(\Delta t\) muito pequeno, a energia \(\Delta E\) seria, mais uma vez, enorme. Assim, a corrida não só se tornaria indetectável (por causa do buraco negro), como a sua própria progressão poderia ser inibida pelas interações (medições) necessárias para demarcar cada um desses infinitos segmentos.

Esta análise permite concluir que os paradoxos de Zenão não são meros “truques lógicos”, superados pela matemática. De facto, eles conduzem a questões físicas profundas que continuam a desafiar a física moderna.

Zenão tinha razão num sentido mais profundo – estava a tocar em algo fundamental sobre os limites da divisibilidade e da observabilidade, algo que as ferramentas puramente matemáticas do cálculo não conseguem abordar completamente. O cálculo infinitesimal resolve apenas o problema matemático da soma da série (convergente), mas não o problema físico da observabilidade em escalas infinitesimais.

As escalas de Planck são o limite físico da “super-tarefa” – definem o ponto onde a “super- tarefa” de Zenão deixa de ser apenas uma abstração matemática e colide com os limites da física. É fascinante pensar que, ao considerar as implicações da mecânica quântica e da relatividade geral nessas escalas, o paradoxo da dicotomia (e a necessidade de “medir” passos cada vez menores) aponta para os mesmos desafios que a gravitação quântica tenta resolver, ainda sem sucesso.

De facto, a tentativa de medir escalas de Planck com (super)precisão revela limitações nas teorias atuais. Uma possibilidade é considerar que o espaço-tempo possa ser quantizado (discreto) em unidades do comprimento e tempo de Planck. A estrutura do espaço-tempo é desconhecida e sem sentido abaixo destas escalas. O princípio da incerteza, combinado com os efeitos gravitacionais previstos pela relatividade geral, sugere que o espaço-tempo nas escalas de Planck pode não ser contínuo e suave como imaginamos. Em vez disso, pode ser discreto, “granular” ou até mesmo possuir uma estrutura mais exótica que ainda não compreendemos.

É aqui que a teoria da gravitação quântica se torna crucial. O princípio da incerteza, ao exigir energias altíssimas para medir distâncias e tempos muito pequenos, amplifica os efeitos gravitacionais. No limite das escalas de Planck, essas energias distorcem o espaço-tempo de tal forma que tornam medições precisas impossíveis. Isso sugere que os conceitos de espaço e tempo contínuos podem falhar nessas escalas, e que uma descrição completa da realidade requer uma teoria que unifique a mecânica quântica e a relatividade geral – uma teoria da gravitação quântica.

As escalas de Planck representam, portanto, o limiar da nossa compreensão atual e um campo aberto à exploração teórica.

Em resumo, a perspetiva é que os paradoxos de Zenão, longe de estarem resolvidos, são uma profecia de que a nossa intuição sobre um espaço-tempo contínuo e a nossa capacidade de medição falham nas escalas mais fundamentais do universo, onde a mecânica quântica e a gravidade se tornam inseparáveis. É uma excelente demonstração de como a filosofia pode continuar a informar e a ser informada pela ciência.