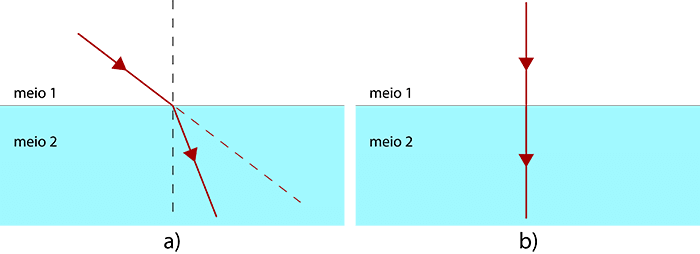
Se a incidência da luz for oblíqua, a refração é acompanhada de mudança de direção (figura 1a), o que não ocorre se a incidência for perpendicular (figura 1b).

Índice de refração

Oticamente, um meio homogéneo e transparente é caracterizado pelo seu índice de refração absoluto. O índice de refração absoluto ( n ) de um meio, para determinada luz monocromática, é a razão entre a velocidade da luz no vazio ( c ) e a velocidade da luz no meio em questão (v ):

\[n=\frac{c} {v}\]

O índice de refração n é adimensional e maior que a unidade, para qualquer meio material, visto que c ; v. Pela equação anterior, o índice de refração do vazio é igual a 1. Para o ar, o índice de refração é praticamente igual a 1, pois a velocidade de propagação da luz no ar é aproximadamente igual à velocidade de propagação no vazio.

leis da refração da luz

Consideremos um raio de luz monocromática propagando-se de um meio de índice de refração n₁ para um outro meio com maior índice de refração, n₂ (Figura 1). Seja i o ângulo de incidência. Devido à refração na interface dos dois meios, o raio incidente dá origem a um raio refratado que se propaga no segundo meio. O raio refratado forma com a normal um ângulo R, denominado ângulo de refração.

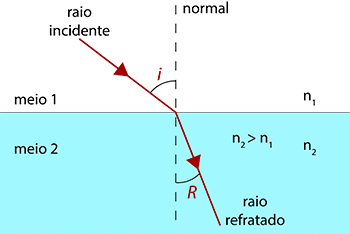
• Se n₁ < n₂ , o ângulo de incidência ( i ) será maior que o ângulo de refração ( R ).
• Se n₁ > n₂ , o ângulo de incidência ( i ) será menor que o ângulo de refração ( R ).
• Se n₁ = n₂ , o ângulo de incidência ( i ) será igual ao ângulo de refração ( R ).

A refração da luz é regida por duas leis:

1. ª Lei: O raio incidente, o raio refratado e a normal à superfície de separação dos dois meios pertencem ao mesmo plano.
2. ª Lei ou Lei de Snell-Descartes: Os ângulos de incidência e de refração satisfazem a condição:

\[ {n_1}\sin \left( i \right) = {n_2}\sin \left( R \right)\]

Assim, se n₂ > n₁, então sin( R ) < sin( i ), resultando R < i. Portanto, para incidência oblíqua da luz, quando esta passa de um meio com menor índice de refração para outro com maior índice, o raio luminoso aproxima-se da normal.

Podemos, também, escrever a lei de Snell-Descartes na forma:

\[ {n_{21} } = \frac{ { {n_2} } } { { {n_1} } } = \frac{ {\sin \left( i \right)} } { {\sin \left( R \right)} } \]

Em que n₂₁ é o índice de refração relativo do meio 2 em relação ao meio 1.

Reflexão total

Quando luz monocromática se propaga de um meio com menor índice de refração para um de maior índice de refração, não existe nenhuma restrição à ocorrência da refração (figura 3). Para incidência normal, o raio refratado é perpendicular à interface dos dois meios (figura 3a). Em incidência oblíqua (i > 0°), o raio luminoso aproxima-se da normal, tendo-se R < i (figura 3b). Para valores crescentes do ângulo de incidência, verifica-se que, à medida que este se aproxima de 90° (incidência razante), o ângulo refratado (R) tende para um valor máximo L, denominado ângulo limite (figura 3c).

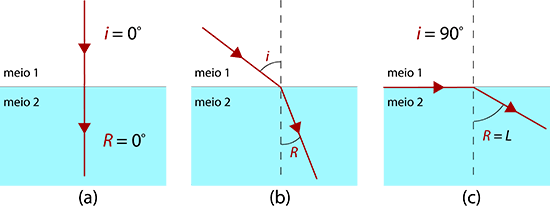
Aplicando a Lei de Snell-Descartes ao caso da refração limite entre dois meios de índices de refração n₁ e n₂ > n₁, obtém-se sucessivamente:

\[{n_1}\sin \left( i \right) = {n_2}\sin \left( R \right)\]

\[{n_1}\sin \left( {90} \right) = {n_2}\sin \left( L \right)\]

\[\sin \left( L \right) = \frac{ { {n_1} } } { { {n_2} } }\]

Sendo n₁ < n₂, podemos escrever:

\[\sin \left( L \right) = \frac{ { {n_{menor} } } } { { {n_{maior}} } }\]

\[L = \arcsin \left( {\frac{ { {n_{menor} } } } { { {n_{maior} } } } } \right)\]

Quando luz monocromática se propaga de um meio com maior índice de refração para outro de menor índice de refração, nem todo o raio luminoso sofre refração. Esta situação corresponde à propagação da luz do meio 2 para o meio 1 (n₁ < n₂). Em incidência normal (Figura 4a), continua a não haver desvio do raio refratado em relação ao incidente. Para incidência oblíqua (Figura 4b), contudo, o raio luminoso afasta-se da normal (R > i). Aumentando gradualmente o ângulo de incidência, o raio refratado aproxima-se da direção razante. Neste caso, a refração limite ocorre para um ângulo de incidência i = L (Figura 4c), para o qual o ângulo de refração atinge o valor máximo de 90°.

No entanto, para este sentido de propagação, ou seja, do meio com maior índice de refração para o de menor, o ângulo de incidência pode ser maior que o ângulo limite. Quando isto ocorre, não há refração e a luz sofre o fenómeno de reflexão total (Figura 4d).

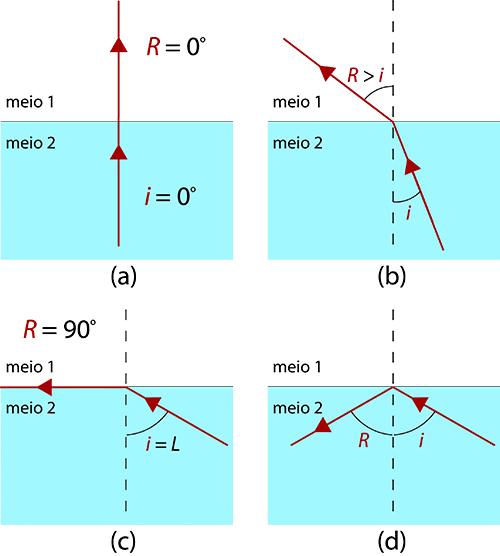
Assim, para haver reflexão total, são necessárias duas condições:

1. ª - Sentido de propagação da luz: do meio com maior índice de refração para o de menor;
2. ª - Ângulo de incidência maior que o ângulo limite: i > L.

Materiais relacionados disponíveis na Casa das Ciências:

1. Comunicações longas, de Rogério Nogueira;
2. Refração, de David Harrison;
3. Refração de ondas, de Vladimir Vašcák;
4. Ondas e índice de refração, de Thomas Fleisch;
5. Índice de refração e ângulo crítico, de Thomas Fleisch;
6. Lentes e espelhos, de Don Ion;
7. Ótica - lentes e espelhos, de Gilbert Gastebois;
8. Espelhos e lentes esféricos, de B. Surendranath Reddy.