Notas

A superfície cónica definida por $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0$ tem o vértice na origem de um referencial tridimensional, ortonormado (em relação ao qual se definiu a equação) e é simétrica em relação aos planos coordenados.

Observe-se ainda que as equações (canónicas) $\frac{x^2} {a^2}-\frac{y^2} {b^2}+\frac{z^2} {c^2}=0$ ou $\frac{x^2} {a^2}-\frac{y^2}{b^2}-\frac{z^2} {c^2}=0$ ou etc. (no primeiro membro, dois coeficientes com um sinal e o terceiro com sinal diferente) também representam superfícies cónicas de vértice em $O$, apesar de terem outro eixo.

Atendendo a que a equação inicial da superfície cónica $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0$ se pode escrever na forma $z^2=c^2\left(\frac{x^2} {a^2}+\frac{y^2} {b^2}\right)$ ou ainda na forma equivalente $z=\pm\sqrt{c^2\left(\frac{x^2} {a^2}+\frac{y^2} {b^2}\right)}$, cada uma destas equações $z=\sqrt{c^2\left(\frac{x^2} {a^2}+\frac{y^2} {b^2}\right)}$ e $z=-\sqrt{c^2\left(\frac{x^2} {a^2}+\frac{y^2} {b^2}\right)}$ define uma hemisuperfície cónica, respetivamente, a superior e a inferior (relativamente ao plano coordenado $XOY$).

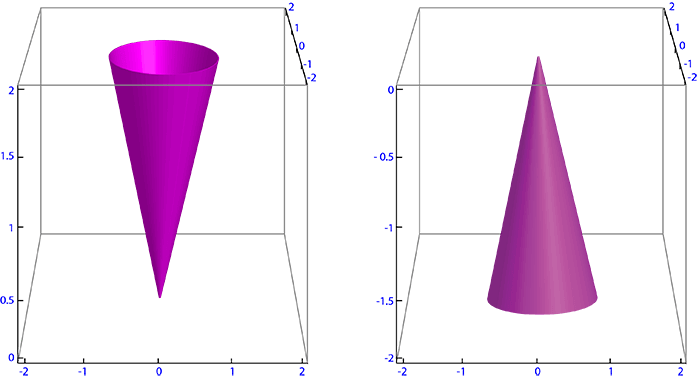
As secções paralelas ao plano coordenado $XOY$ são elipses (circunferências quando $a=b$, caso em que se tem um cone de revolução ou cone circular reto) definidas por $\frac{x^2}{a^2}+\frac{y^2}{b^2}=k$.

As secções planas paralelas aos outros planos coordenados são hipérboles definidas por $\frac{x^2} {a^2}-\frac{z^2} {c^2}=k$ ou $\frac{y^2} {b^2}-\frac{z^2} {c^2}=k$.

Materiais relacionados disponíveis na Casa das Ciências:

1. Cónicas, de Michael R. Gallis.