A capacidade é uma grandeza que só depende da geometria do condutor. Por exemplo, a capacidade de uma esfera condutora é \(4\pi {\varepsilon _0}R\), sendo \({\varepsilon _0}\) permitividade eléctrica do vazio e R o raio da esfera condutora. A unidade SI de capacidade é o farad (F): 1 F é a capacidade de um condutor que estando ao potencial e 1 V está carregado com 1 C.

Condensadores e capacidade do condensador

Consideremos um sistema formado por dois condutores eletricamente carregados, com cargas simétricas. A disposição e geometria dos condutores é tal que toda a linha de campo que parte de um deles chega ao outro. Este tipo de arranjo espacial de condutores designa-se por geometria de influência total, e ao sistema de condutores por condensador. Um condensador é utilizado para armazenar carga eléctrica em circuitos elétricos. A quantidade de carga eléctrica armazenada é diretamente proporcional à diferença de potencial dos condutores que formam o condensador:

\[C = \frac{Q} {\Delta V}\]

sendo \(Q\) o módulo da carga existente num dos condutores, e \(\Delta V\) a diferença de potencial entre os condutores.

Como exemplos podemos considerar:

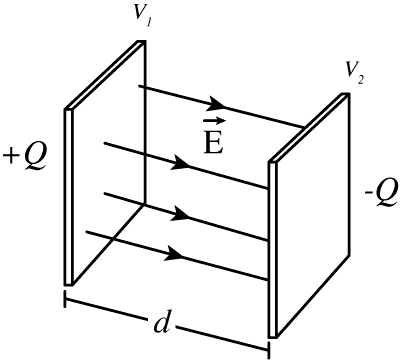
• O condensador plano é constituído por duas placas condutoras planas e paralelas entre si, de área S e distanciadas de d. Mostra-se que o campo elétrico na região central do espaço entre as placas pode considerar-se uniforme. Contudo, na região periférica entre as placas o campo elétrico não é uniforme - efeito de bordo. Desprezando o efeito de bordo, a capacidade do condensador plano é \(C = \frac{S \epsilon_0} {d}\).







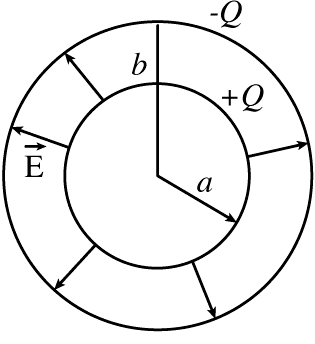
• O condensador cilíndrico é constituído por um condutor cilíndrico coaxial com uma superfície condutora, cuja capacidade, por unidade de comprimento é \(C = \frac{2 \pi \epsilon_0} {ln(\frac{a} {b})}\)em que \(a\) e \(b\) são os raios do cilindro interior e exterior respetivamente.







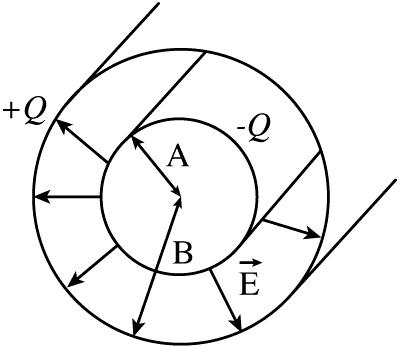
• O condensador esférico é constituído por uma esfera condutora centrada na cavidade esférica de outro condutor, cuja capacidade é \(C = \frac{4 \pi \epsilon_0}{\frac{1}{a} - \frac{1}{b}}\) em que \(a\) e \(b\) são os raios da esfera interior e exterior respetivamente.

A capacidade dos condensadores utilizados nos circuitos eletrónicos toma valores que são submúltiplos do farad; em geral, temos condensadores de picofarad (1 pF=10^-12 F) , nanofarad (1 nF = 10^-9 F) e microfarad (1 µF = 10^-6 F).

Para carregar um condensador, é preciso que uma fonte de força eletromotriz, ligada no circuito que contém o condensador, realize trabalho contra as forças de campo elétrico para transportar carga eléctrica para cada um dos condutores do condensador. A energia gasta neste processo fica armazenada no sistema sob a forma de energia potencial eléctrica que pode ser utilizada posteriormente. A energia contida num condensador, cuja carga é Q e a diferença de potencial entre os condutores é \(\Delta V\), é dada por¹:

\[E = \frac{1} {2} Q \Delta V\]

Que pode ser reescrita à custa da capacidade do sistema nas seguintes formas:

\[E = \frac{1} {2}C(\Delta V)^2 = \frac{1} {2} \frac{Q^2} {C}\]

Efeito da introdução de um dielétrico num condensador

Um isolador ou dielétrico inserido entre os condutores de um condensador, permite que o sistema possa armazenar a mesma carga eléctrica mas a uma diferença de potencial inferior, aumentando, deste modo, a capacidade do condensador. O aumento da capacidade do condensador com dielétrico depende da natureza do dielétrico, que é caracterizada pela sua permitividade eléctrica ε. Deste modo, sendo \(C_0\) a capacidade do condensador sem dielétrico, a capacidade do condensador, com a mesma geometria mas preenchido por um dielétrico de permitividade ε é:\(C = εC_0\).

Materiais relacionados disponíveis na Casa das Ciências:

1. Condensadores planos, de Manuela Assis e Maria Carvalhal;
2. Oscilações elétricas num condensador, de Isabelle Tarride;
3. Carga e descarga de um condensador, de Isabelle Tarride;
4. Carga e descarga de um condensador II, de Isabelle Tarride.