Coeficiente de correlação amostral
📧
- Faculdade de Ciências da Universidade de Lisboa
Referência Martins, E.G.M., (2014) Coeficiente de correlação amostral, Rev. Ciência Elem., V2(2):042
DOI http://doi.org/10.24927/rce2014.042
Palavras-chave Coeficiente; correlação; amostral;
Resumo
A Correlação entre duas variáveis de tipo quantitativo descreve a associação entre essas variáveis.
Na presença de um conjunto de dados bivariados o primeiro passo na análise desses dados é representá-los num diagrama de dispersão. A forma da nuvem de pontos, representada no diagrama, pode mostrar uma associação linear entre as duas variáveis, que pode ser expressa numericamente pelo coeficente de correlação amostral de Pearson ou pelo seu quadrado que se chama coeficiente de determinação.
O Coeficiciente de correlação amostral de Pearson, representado por r, é uma medida da direção e grau com que duas variáveis, de tipo quantitativo, se associam linearmente.
Se representarmos por (x,y)={\(({\rm{x_{i},y_{i} } })\)}, com i = 1,...,n, uma amostra de dados bivariados, o coeficiente de correlação amostral de Pearson calcula-se a partir da seguinte fórmula:
\[{\rm{r = } }\frac{ {\sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{n} } ( { {\rm{x}}_{\rm{i} } } {\rm{ - \bar x)(} } { {\rm{y}}_{\rm{i} } } {\rm{ - \bar y)} } } }{ {\sqrt {\sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{n} } { { { {\rm{(} } { {\rm{x}}_{\rm{i} } } {\rm{ - \bar x)} } }^{\rm{2} } }\sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{n} } { { {({ {\rm{y} }_{\rm{i} } } {\rm{ - \bar y)} } }^{\rm{2} } } } } } } } {\rm{\quad\quad\quad onde\quad\quad\quad\bar x} } = \frac{ {\sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{n} } { { {\rm{x}}_{\rm{i} } } } } } { {\rm{n} } } {\rm{\quad\quad\quad e \quad\quad\quad\bar y} } = \frac{ {\sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{n}} { { {\rm{y} }_{\rm{i} } } } } } { {\rm{n} } }\]
ou seja, o coeficiente de correlação r para o par de variáveis (x,y) é o quociente entre a covariância amostral das variáveis x e y e o produto dos desvios padrões respetivos:
\[{\rm{r} } = \frac{ { {\rm{Cov(x} } {\rm{,y)} } } } { { { {\rm{s} }_{\rm{x} } } { {\rm{s} }_{\rm{y} } } } }\]
Podem-se mostrar as seguintes propriedades do coeficiente de correlação r:
- O coeficiente de correlação assume valores entre -1 e 1.
- Quanto maior for o valor de r, em módulo, maior será o grau de associação linear entre as variáveis.
- Um valor de r positivo indica uma associação linear positiva entre as duas variáveis, isto é, quando os valores de uma das variáveis aumentam, existe tendência para que os valores da outra variável também aumentem. Um valor de r negativo indica uma associação linear negativa entre as duas variáveis, isto é, quando os valores de uma das variáveis aumentam, existe tendência para que os valores da outra variável diminuam.
- O coeficiente de correlação não é uma medida resistente, isto é, pode ser influenciado pela existência nos dados de alguns valores estranhos ou outliers, ou seja, valores muito maiores ou menores que os restantes, pelo que deve ser interpretado com o devido cuidado. A representação prévia dos dados num diagrama de dispersão, antes de proceder ao cálculo do coeficiente de correlação, permite detetar a existência de outliers.
Apresentam-se a seguir alguns exemplos de representações gráficas de conjuntos de dados relativos a notas obtidas em dois exames por alunos de 6 classes e respetivos coeficientes de correlação (Adaptado de Rossman, A. J. (1996)):

A visualização dos gráficos anteriores leva-nos a supor que entre os dois exames se possa admitir o seguinte tipo de associação:
| Forte | Moderada | Fraca | |
| Positiva | E | A | B |
| Negativa | C | D | F |
O cálculo do coeficiente de correlação, que se apresenta na tabela seguinte, completa a informação da tabela anterior:
| Classe | Correlação |
| A | 0.71 |
| B | 0.47 |
| C | -0.99 |
| D | -0.72 |
| E | 0.99 |
| F | -0.47 |
Repare-se que apenas nos casos em que | \({\rm{r}}\) | é muito elevado faz sentido falar de associação linear forte, como é observado nos casos C e E em que o gráfico de dispersão aponta para isso.
Num contexto de regressão linear simples, em que a variável explanatória é x e a variável resposta é y, o coeficiente de determinação r2 dá a percentagem de variabilidade dos y's que fica explicada em função da variabilidade dos x’s. Assim, embora aparentemente um valor de r à volta de 0,7 possa parecer elevado, na realidade, é maior a percentagem de variabilidade que fica por explicar (100-49)% do que a explicada (100x0,72)%, pelo que um valor de r naquela ordem de grandeza corresponde a um relacionamento moderado.
Mais uma vez se chama a atenção para que o coeficiente de correlação só mede a intensidade com que duas variáveis se associam linearmente. Como se verifica no exemplo seguinte
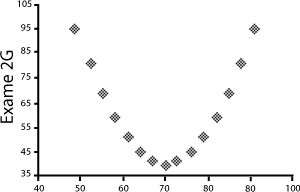
existe uma forte associação entre os dados do Exame1 e os dados do Exame2 e no entanto o coeficiente de correlação vem igual a 0.
Correlação e relação causa-efeito É importante não confundir associação, medida pelo coeficiente de correlação, com relação causa-efeito. Um diagrama de dispersão e uma correlação não provam a existência de uma relação causa-efeito. Podem existir outras variáveis, que não são estudadas, mas influenciam as que estão a ser estudadas e que são conhecidas como variáveis lurking ou confounding (variáveis de confundimento).
O coeficiente de correlação amostral r pode ser usado para estimar o coeficiente de correlação populacional \(\rho\).
Referências
- 1 Murteira, B., Ribeiro, C. S., Silva, J. A., Pimenta, C. (2002) – Introdução à Estatística. McGraw-Hill de Portugal, Lda. ISBN:972-773-116-3
- 2 Rossman, A.J. (1996) - Workshop Statistics: Discovery with data. New York: Springer-Verlag
- 3 Pestana, D., Velosa, S. (2010) – Introdução à Probabilidade e à Estatística, Volume I, 4ª edição, Fundação Calouste Gulbenkian. ISBN: 978-972-31-1150-7. Depósito Legal 311132/10.
Este artigo já foi visualizado 6799 vezes.



