Do tipo \(\sin x=\sin\alpha\)

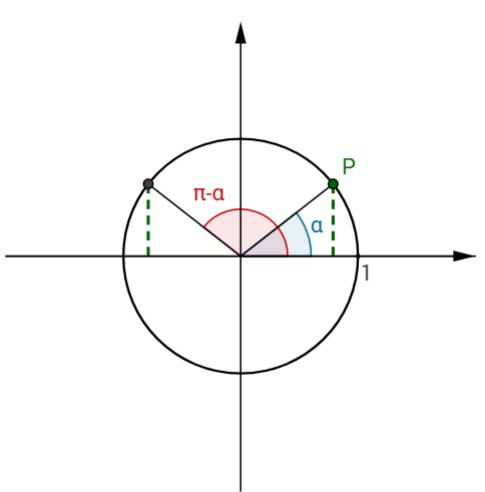
Considerando a aplicação ao lado podemos alterar a amplitude de \(\alpha\), movendo \(\qquad\) o ponto P, e verificar as soluções deste tipo de equação para qualquer ângulo \(\alpha\). \(\qquad\) Facilmente se verifica que as soluções da equação \(\sin x=\sin\alpha\) são: \(x=\alpha+2k\pi\quad \) ou \(\quad x=\pi-\alpha+2k\pi\), com \(\, k \in \mathbb{Z}.\)

Do tipo \(\cos x=\cos\alpha\)

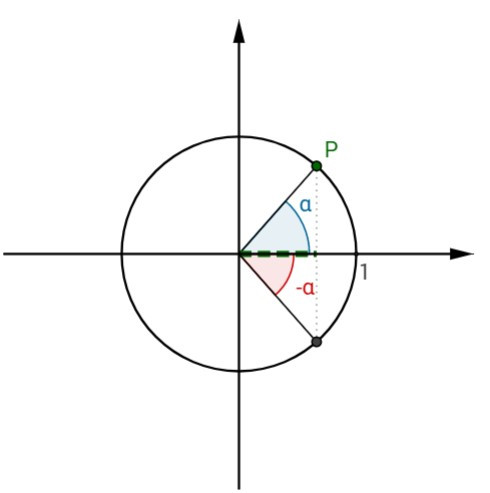
\(\quad\) Considerando a aplicação podemos alterar a amplitude de \(\alpha\), movendo o ponto P, \(\quad\) e verificar as soluções deste tipo de equação para qualquer ângulo \(\alpha\). \(\quad\) Facilmente se verifica que as soluções da equação \(\cos x=\cos\alpha\) são: \(\quad\) \(x=\alpha+2k\pi \quad\) ou \(\quad x=-\alpha+2k\pi\), com \(\, k \in \mathbb{Z}\) \(\quad\) Ou de forma condensada \(x=\pm\,\alpha+2k\pi, \quad k \in \mathbb{Z}\).

Do tipo \(\tan x=\tan\alpha\)

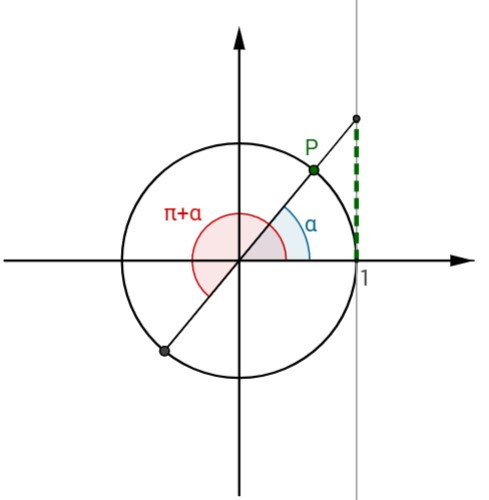
Considerando a aplicação ao lado podemos alterar a amplitude de \(\alpha\), movendo \(\qquad\) o ponto P, e verificar as soluções deste tipo de equação para qualquer ângulo \(\alpha\). \(\qquad\) Facilmente se verifica que as soluções da equação \(\tan x=\tan\alpha\) são: \(\qquad\) \(x=\alpha+2k\pi \quad\) ou \(\quad x=\pi+\alpha+2k\pi \), com \(\, k \in \mathbb{Z}\)

Do tipo \(\sin x=\cos\alpha \,\) e \(\, \cos x=\sin\alpha\)

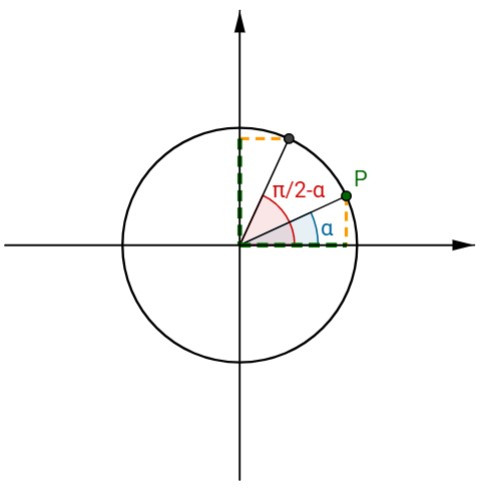
\(\quad\) Considerando a aplicação podemos alterar a amplitude de \(\alpha\), movendo o ponto P, \(\quad\) e verificar as soluções deste tipo de equação para qualquer ângulo \(\alpha\). \(\quad\) Facilmente se observa na aplicação que: \(\quad\) \(\displaystyle \cos \alpha=\sin\left(\frac{\pi}{2}-\alpha\right)\quad \) e que \(\quad \displaystyle \sin \alpha=\cos\left(\frac{\pi}{2}-\alpha\right)\) \(\quad\) Portanto a resolução de uma equação do tipo \(\sin x=\cos\alpha\) é equivalente à resolução da equação \(\displaystyle\sin x=\sin \left(\frac{\pi}{2}-\alpha\right)\). Usando o referido num dos pontos anteriores as soluções são: \(\displaystyle x=\frac{\pi}{2}-\alpha+2k\pi \quad\) ou \(\quad \displaystyle x=\frac{\pi}{2}+\alpha+2k\pi\), com \(k \in \mathbb{Z}\). \(\quad\) Já a resolução de uma equação do tipo \(\cos x=\sin\alpha\) é equivalente à resolução da equação \(\displaystyle \cos x=\cos \left(\frac{\pi}{2}-\alpha\right)\). Usando o referido num dos pontos anteriores as soluções são: \(\displaystyle x=\frac{\pi}{2}-\alpha+2k\pi \quad\)ou\(\quad \displaystyle x=-\left(\frac{\pi}{2}-\alpha\right)+2k\pi\), com \(k \in \mathbb{Z}\)

Exemplos

\(\triangleright \quad 2\sin x-1=0\)

O primeiro passo será simplificar a equação:

\(\displaystyle 2\sin x-1=0 \, \Leftrightarrow \, \sin x=\frac{1}{2}\)

A figura 1 esclarece o próximo passo: calcular as soluções da equação no intervalo \(\left[0,2\pi\right]\).

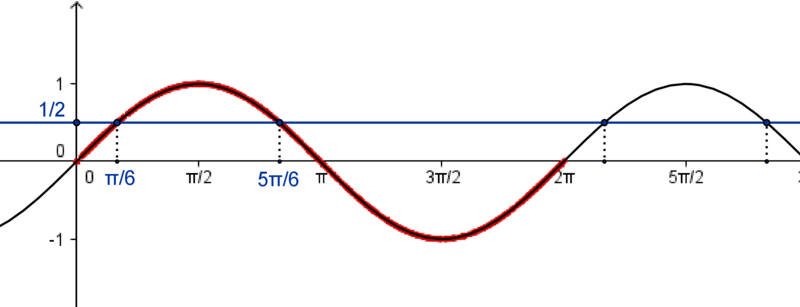
Uma dessas soluções é \(\displaystyle x=\frac{\pi}{6}\) pois, \(\displaystyle \sin\frac{\pi}{6}=\frac{1}{2}\).

Outra solução é \(\displaystyle x=\pi-\frac{\pi}{6}=\frac{5\pi}{6}\) pois, \(\displaystyle \sin \frac{5\pi}{6}=\frac{1}{2}\).

Considerando agora a periodicidade da função seno, de período \(2\pi\), temos então todas as soluções da equação inicial:

\(\displaystyle x=\frac{\pi}{6}+2k\pi \quad \) ou \(\quad \displaystyle x=\frac{5\pi}{6}+2k\pi\), com \( k \in \mathbb{Z}\).

\(\triangleright \quad \sin 3x=\sin x\)

Usando o que vimos anteriormente sobre equações do tipo \(\sin x=\sin\alpha\) esta equação resolve-se facilmente:

as soluções de \(\displaystyle \sin 3x=\sin x \quad \) são \(\quad 3x=x+2k\pi\quad \) ou \(\quad 3x=\pi-x+2k\pi\), com \( k \in \mathbb{Z}\), ou seja,

\(x=k\pi \quad \) ou \( \quad \displaystyle x= \frac{\pi}{4} + \frac{k\pi}{2}\), com \( k \in \mathbb{Z}\).

\(\triangleright \displaystyle \quad \cos 4x=\sin \left(\frac{\pi}{5}-x\right)\)

Mais uma vez podemos usar o que vimos anteriormente, neste caso sobre as equações do tipo \(\cos x=\sin\alpha\). Como já havíamos concluído \(\displaystyle \cos \alpha=\sin \left(\frac{\pi}{2}-\alpha\right)\) portanto:

\(\displaystyle \cos \,4x=\sin\left(\frac{\pi}{2}-4x\right)\) ou seja, \(\displaystyle \cos \,4x=\sin \left(\frac{\pi}{5}-x\right)\) é equivalente a \(\displaystyle \sin\left(\frac{\pi}{2}-4x\right)=\sin \left(\frac{\pi}{5}-x\right)\).

Ora, as soluções de\(\displaystyle \sin\left(\frac{\pi}{2}-4x\right)=\sin \left(\frac{\pi}{5}-x\right)\quad \) são \(\quad \displaystyle \frac{\pi}{2}-4x=\frac{\pi}{5}-x+2k\pi \quad \) ou \(\quad \displaystyle \frac{\pi}{2}-4x=\pi-\left(\frac{\pi}{5}-x\right)+2k\pi\), com \( k \in \mathbb{Z}\), ou seja, obtemos todas as solução na forma:

\(\displaystyle x=\frac{\pi}{10}-\frac{2k\pi}{3} \quad \) ou \(\quad \displaystyle x= -\frac{3\pi}{50} - \frac{2k\pi}{5}\), com \( k \in \mathbb{Z}\).

\(\triangleright \quad 2\cos 3x+\sqrt{2}=0 \, \) no intervalo \(\, \left]-\pi/4, \pi\right]\)

Começamos por simplificar a equação trigonométrica,

\(\displaystyle 2\cos 3x+\sqrt{2}=0 \, \Leftrightarrow \, \cos 3x=-\frac{\sqrt{2}}{2}\).

A figura 2 mostra as duas soluções da equação no intervalo \(\left]-2\pi, 2\pi\right[\) que são

\(\displaystyle 3x=-\frac{3\pi}{4} \,\mbox{e}\quad 3x=\frac{3\pi}{4}\), pois \(\displaystyle \cos \left(-\frac{3\pi}{4}\right)=\cos \frac{3\pi}{4}=-\frac{\sqrt{2}}{2}\).

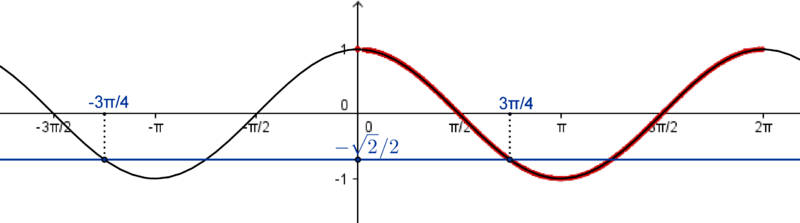
Assim, considerando a periodicidade da função cosseno, de período \(2\pi\), temos então todas as soluções da equação \(\displaystyle \cos 3x=-\frac{\sqrt{2}}{2}\),

\(\displaystyle 3x=-\frac{3\pi}{4}+2k\pi \quad \) ou \(\quad \displaystyle 3x=\frac{3\pi}{4}+2k\pi \), com \( k \in \mathbb{Z}\), ou seja,

\(\displaystyle x=-\frac{\pi}{4}+\frac{2k\pi}{3} \quad \) ou \(\quad \displaystyle x=\frac{\pi}{4}+\frac{2k\pi}{3}\), com \( k \in \mathbb{Z}\).

Como queremos apenas determinar as raízes da equação trigonométrica no intervalo \(\displaystyle \left]-\frac{\pi}{4}, \pi\right]\)) consideramos então alguns valores para \(k\):

para \(k=-1\), vem \(\quad \displaystyle x=-\frac{11\pi}{12} \) ou \(\quad \displaystyle x=-\frac{5\pi}{12} \qquad \), para \(\quad k=0\), \(\quad \displaystyle x=-\frac{\pi}{4} \) ou \(\quad \displaystyle x=\frac{\pi}{4} \qquad \), para \(\quad k=1\), \(\displaystyle x=\frac{5\pi}{12} \) ou \(\quad \displaystyle x=\frac{11\pi}{12} \qquad \), e para \(\quad k=2\), \(\displaystyle x=\frac{13\pi}{12} \) ou \(\quad \displaystyle x=\frac{19\pi}{12}\)

Portanto, as soluções da equação trigonométrica inicial no intervalo \(\displaystyle \left]-\frac{\pi}{4}, \pi\right]\) são \(\displaystyle x= \left\{ \frac{\pi}{4}, \frac{5\pi}{12}, \frac{11\pi}{12} \right\}\).