Seno de um ângulo agudo
📧 , 📧
- * CMUP/ Universidade do Porto
- ɫ CMUP/ Universidade do Porto
Referência Tavares, J., Geraldo, A., (2015) Seno de um ângulo agudo, Rev. Ciência Elem., V3(1):016
DOI http://doi.org/10.24927/rce2015.016
Palavras-chave ângulo; amplitude; agudo;
Resumo
Definição
Para definir o seno de um ângulo agudo de amplitude α є ]0,90°[, fazemos a construção seguinte que se ilustra nas
figuras:
- escolhemos um ponto qualquer C num dos lados do ângulo. Por exemplo, no applet, escolhemos o ponto C num dos lados do ângulo (no applet escolhemos o lado horizontal);
- construímos a perpendicular a esse lado que passa em C;
- essa perpendicular intersecta o outro lado em B e, desta forma, obtemos o triângulo retângulo representado na figura - o triângulo ACB, retângulo em C.
O seno de α define-se agora através da razão
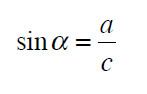
onde a é o comprimento do cateto BC e c é o comprimento da hipotenusa AB.
Note ainda que o valor de sin α não depende do ponto C escolhido no passo nº1. De facto, variando C obtemos triângulos retângulos, semelhantes entre si, e portanto, a razão a/c não muda.
Nota
Para qualquer ângulo agudo de amplitude α є ]0,90º[ , 0 < sin α < 1.
Exemplos
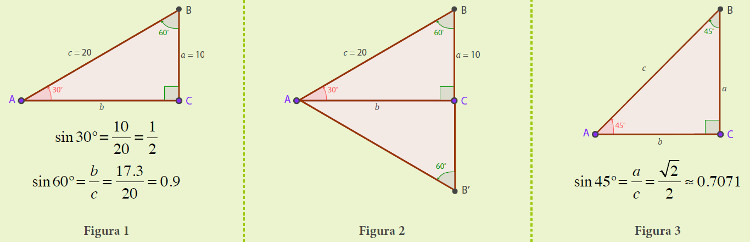
Para calcular o seno de um ângulo agudo podemos pois usar um triângulo retângulo qualquer. Por exemplo, na Figura 1 usamos
um triângulo retângulo cuja hipotenusa é c = 20, para calcular o seno de 30°. Como é claro da Figura 2, o
cateto a é metade da hipotenusa, isto é, a = 10 e portanto
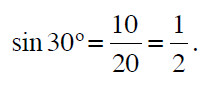
Por outro lado, pelo teorema de Pitágoras, c2 = a2 + b2, e substituindo os valores de c = 20 e a = 10, obtemos b = √(400 −100) = 10√3 . Portanto
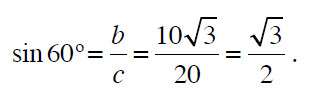
Na Figura 3 usamos um triângulo retângulo isósceles (os dois catetos com o mesmo comprimento, a = b), para calcular o seno de 45°. Pelo teorema de Pitágoras c2 = a2 + b2 = 2a2, uma vez que a = b . Portanto, c = √(2a) e daí que
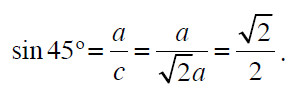
Este artigo já foi visualizado 3454 vezes.



