Se representarmos o resultado da observação da variável quantitativa, sobre todos os N elementos da população, por \(\rm{x_{1}, x_{2}, ..., x_{N}}\), então o valor médio, que se representa pela letra grega \(\mu\), obtém-se a partir da expressão

\[\mu = \frac{\sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{N} } { {\rm{x_{i}} } } } { {\rm{N} } }\]

Uma variável de tipo quantitativo, que se observa sobre todos os elementos da população finita, é uma variável aleatória discreta (com suporte finito). Assim, o valor médio de uma variável aleatória discreta é a média aritmética ponderada de todos os valores que a variável pode assumir, em que os coeficientes de ponderação são as probabilidades de assumir esses valores.

Como se identifica população com a variável aleatória, correspondente à característica em estudo sobre a população (desde que quantitativa), tanto se pode falar em valor médio da população como da variável aleatória.

Mais genericamente, se tivermos uma variável aleatória X discreta (com um número finito ou infinito numerável de valores distintos) em que a distribuição de probabilidades é o conjunto \(\{ {\rm{x_{i},p_{i}}}\}\), i = 1, 2, ...,M ou \(\{ {\rm{x_{i},p_{i} }}\}\), i=1, 2, ..., então

\[\mu = \sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{M}} { {\rm{x_{i} } \times {\rm{p_{i} } } } } \quad {\rm{ou}}\quad \mu = \sum\limits_{ {\rm{i} } = {\rm{1} } }^{\rm{\infty} } { {\rm{x_{i} } \times {\rm{p_{i} } } } } \quad ({\rm{exigindo-se \ que \ }} \sum\limits_{ {\rm{i} } = {\rm{1}}}^{\rm{\infty}} {|{\rm{x_{i} }| \times {\rm{p_{i} } } } } < \infty)\]

Por exemplo, se considerarmos a população constituída pelo número de irmãos de todos os 28 alunos da turma A do 8º ano da escola ABC, no ano letivo 2011-2012,

\[1 \quad 2 \quad 1 \quad 0 \quad 2 \quad 3 \quad 2 \quad 1 \quad 1 \quad 4 \quad 2 \quad 1 \quad 0 \quad 2 \quad 1 \quad 1 \quad 3\]

\[\quad 2 \quad 3 \quad 1 \quad 1 \quad 2 \quad 1 \quad 3 \quad 2 \quad 1 \quad 0 \quad 1\]

podemos falar na variável aleatória X, que representa o “número de irmãos” de um aluno escolhido ao acaso na referida turma, com a seguinte distribuição de probabilidades:

Então, o valor médio da população ou da variável aleatória X será igual a

\[\mu = \frac{1 + 2 + 1 + 0 + 2 + 3 + 2 + 1 + 1 + 4 + 2 + 1 + 0 + 2 + 1 + 1 + 3 + 2 + 3 + 1 + 1 + 2 + 1 + 3 + 2 + 1 + 0 + 1}{28}\]

\(\ \ \approx 1,6\)

ou

\(\mu = 0 \times \frac{3}{28} + 1 \times \frac{12}{28} + 2 \times \frac{8}{28} + 3 \times \frac{4}{28} + 4 \times \frac{1}{28}\)

\(\ \ \approx 1,6\)

Suponhamos agora que num jogo (Adaptado de MANN (1995), página 229 e do Curso de Probabilidade em (http://www.alea.pt), página 24) semelhante à Raspadinha, cada bilhete custa 1 euro e os prémios que se podem ganhar são 500 euros, 23 euros, 13 euros, 7 euros, 3 euros e 1 euro. Cada bilhete tem uma superfície suscetível de ser raspada, a qual revela um dos prémios anteriores ou nenhum prémio. São postos em circulação 6 000 000 bilhetes, de acordo com a seguinte tabela

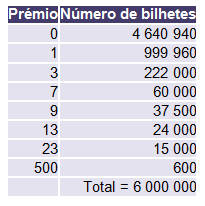
Representando por X a variável aleatória que representa o “lucro de um jogador que faça uma jogada neste jogo”, temos a seguinte distribuição de probabilidades para a variável aleatória X:

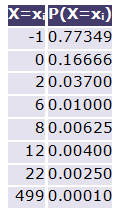
Utilizámos o conceito de Laplace (ver Probabilidade) para obter a distribuição de probabilidades anterior.

O valor médio da variável aleatória X é –0.43659. A interpretação que podemos dar a este resultado é a de que se considerarmos todos os jogadores, cada jogador perde, em média, aproximadamente 44 cêntimos por bilhete.

Se precisarmos de identificar que o valor médio se refere à variável aleatória X, representamos por E(X).

O valor médio é uma medida de localização do centro da distribuição de probabilidades da variável aleatória. Apesar de ser uma medida muito utilizada, tem que se ter as devidas cautelas, pois, tal como a média, é muito sensível a valores muito grandes ou muito pequenos, dizendo-se que é uma medida pouco resistente.

Quando se pretender estimar o parâmetro valor médio de uma variável aleatória, recolhe-se uma amostra de valores assumidos por essa variável e utiliza-se como estimativa a estatística média.