Índice de refração, esse desconhecido (parte I)
📧
- Universidade do Porto
Referência Marques, M.J.B., (2016) Índice de refração, esse desconhecido (parte I), Rev. Ciência Elem., V4(2):011
DOI http://doi.org/10.24927/rce2016.011
Palavras-chave Ótica; Refração; luz; velocidade;
Resumo
Introdução
Desafiado a escrever um
texto
dentro da temática da Ótica, decidi abordar um tema que parece, à
primeira vista, não trazer nada de interessante – o índice de refração.
O índice de refração é muito utilizado no ensino da ótica mas ainda tem
muitos aspetos que são desconhecidos pela maioria dos professores.
O índice de refração é muitas vezes sobre-simplificado, dando-lhe o valor 1,5, que é utilizado até à exaustão1, ficando muitos alunos com a ideia de que é sempre igual a 1,5. Mesmo aquando da explicação qualitativa da separação das cores por um prisma, a dependência do índice de refração do comprimento de onda não é apreendida pela maioria dos alunos. Para além da dependência do comprimento de onda, o valor do índice de refração dos materiais varia quando sujeito à influência de quase todas as grandezas físicas. A simplificação que fazemos ao não considerar a dependência cruzada das grandezas macroscópicas é importante para não complicar demasiado o ensino, mas considero que é necessário consciencializar os alunos que a Física que ensinamos é uma aproximação, que dá resultados ótimos na maioria das situações do dia a dia, mas que é necessário utilizar os efeitos desprezados para explicar como funcionam muitas das aplicações tecnológicas do último século.
Ao longo dos anos tenho usado o índice de refração como um exemplo desta simplificação que temos que utilizar no ensino da Física. Costumo começar por dizer que o índice de refração depende de tudo o que nos ocorrer em termos físicos, desde a simples aplicação de uma força ao material até à própria intensidade da luz.
Um segundo desafio que pus a mim mesmo seria de tentar escrever este artigo sem uma única equação, deixando o estudo mais aprofundado para os mais curiosos através de futuras leituras.
Nesta primeira parte, irei abordar alguns aspetos mais fundamentais do índice de refração, explicitando algumas dependências das características do material em que a luz se propaga. Numa segunda parte, abordarei alguns pontos relativamente à sua dependência de parâmetros físicos externos ao material.
Definição
O índice de refração é
uma propriedade macroscópica, isto é, só pode ser definida quando se faz
a média das ações individuais dos átomos, ou moléculas, num volume que
contém um número muito grande de partículas. Uma forma simplificada de o
definir é como a razão entre a velocidade da luz no vácuo e a velocidade
da luz no material em consideração. Outra definição é baseada no que
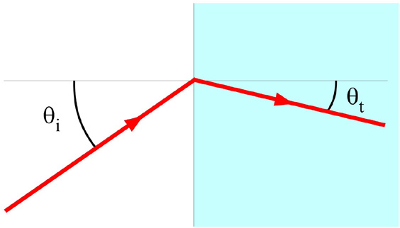
acontece à luz na interface entre dois materiais; aqui, podemos
simplificar usando a lei de Snell, e afirmar que o índice de refração
relativo entre os dois meios é a razão dos senos dos ângulos de
incidência e de refração. Estas duas definições dão o mesmo resultado
para a grande maioria das situações com que nos deparamos, mas são
incompatíveis em algumas situações, como veremos.
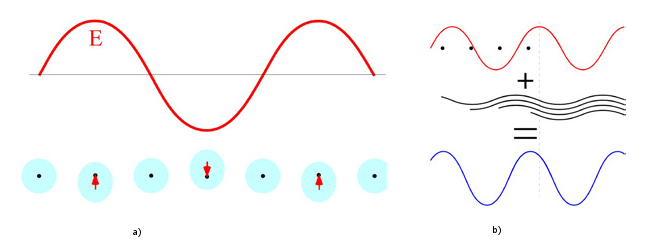
Mas o que se passa a nível atómico e molecular? A onda eletromagnética, ou os fotões se preferirmos a visão mais quântica, encontram um espaço maioritariamente vazio com núcleos e distribuiçõesletrónicas em certas posições, regulares, no caso de meios cristalinos. Por simplicidade, vou abordar o modelo semi-clássico num meio constituído por átomos isolados. O campo elétrico da onda vai induzir uma oscilação na nuvem eletrónica à mesma frequência, devido à força elétrica exercida sobre os eletrões2 (figura 1a). Esta oscilação da nuvem eletrónica vai, por sua vez, emitir uma onda eletromagnética com a mesma frequência, mas com algum atraso. A sobreposição da onda original com esta pequena onda atrasada vai originar uma onda, com a mesma frequência, que viaja ligeiramente mais devagar. Somando a contribuição de todos os átomos, incluindo a sua separação, chegamos à velocidade de propagação da luz dentro de um meio material. Este modelo, ainda que muito simplificado, permite obter alguns resultados interessantes.
- Se os átomos não estiverem distribuídos de forma regular, existe sempre alguma luz que é espalhada noutras direções, dando origem ao que designado é por espalhamento de Rayleigh3.
- Um aumento da densidade de átomos implica uma diminuição da velocidade da luz. Daqui deriva uma lei geral: nos gases, o índice de refração aumenta linearmente com a pressão4.
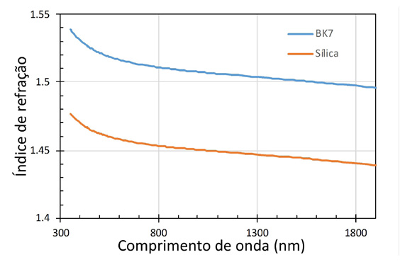
- Se o átomo, ou molécula, for excitado por uma onda próxima de alguma das suas frequências de ressonância, obtém-se uma maior amplitude de oscilação da nuvem eletrónica, e portanto, a contribuição de cada elemento para o índice de refração vai ser mais importante. Como resultado disto, o índice de refração aumenta quando nos aproximamos das linhas de absorção. Como todos os vidros têm forte absorção no ultravioleta, o índice de refração diminui no visível com a aproximação ao infravermelho (dispersão normal)5.
- Num cristal, a presença de outros átomos na vizinhança altera a resposta da nuvem eletrónica a estímulos exteriores. Se o sistema não for isotrópico, a resposta do átomo passa agora a depender da direção do campo elétrico da onda incidente (polarização) dando origem a uma velocidade diferente para cada componente do campo elétrico (birrefringência). Este fenómeno permite manipular os estados de polarização da luz, incluindo a separação de um feixe de luz em dois linearmente polarizados6.
Parte imaginária do índice de refração
Quando
existe absorção no material, podemos considerar que o índice de refração
tem uma parte imaginária. Essa parte imaginária, ao ser incluída na
equação de onda (escrita na forma complexa com uma exponencial
imaginária no lugar do seno ou cosseno), vai dar origem a um termo de
“amortecimento” que corresponde à dissipação de energia. Um ponto
importante é que esta parte imaginária está relacionada, de forma muito
clara, com a parte real do índice de refração, o que permite estimar a
variação da velocidade da luz em função da frequência a partir da
medição do espectro de absorção do material.
Dependência da frequência
Com
vimos, existe uma variação do índice de refração com a frequência, ou
comprimento de onda, que é responsável pela separação das cores na
experiência clássica da dispersão da luz por um prisma (figura 2). No
entanto este efeito apresenta aspetos negativos.
Em primeiro lugar, dá origem à aberração cromática, pela qual uma lente apresenta uma distância focal diferente para cada cor. O nosso olho sofre desta aberração, que é compensada pelo cérebro, pelo que não é significativa a diferença quando utilizamos óculos.
Nas comunicações por fibra ótica, como a distância percorrida no material é elevada, esta dispersão tornase um fator importante. Apesar de ser utilizada luz quase monocromática, a modulação da intensidade dá origem a um alargamento espectral7. As diferentes frequências viajam com velocidades diferentes, e desta forma, alargam o impulso inicial. Se este alargamento temporal for superior à separação entre bits, começamos a ter erros na transmissão8. Quando começamos a tratar da luz localizada no tempo é necessário introduzir duas definições de velocidade da luz: velocidade de fase e velocidade de grupo. A primeira indica a velocidade a que se propaga a onda “sinusoidal”, correspondente aos campos elétrico e magnético, e a segunda, de uma forma simplista, a velocidade com que se propaga o pico do impulso.
Dependência da polarização da luz
Como
vimos, se não houver isotropia dentro do material, cada direção do campo
elétrico (ortogonal à direção de propagação) terá uma velocidade
diferente (n diferente). Na incidência de um feixe inclinado na
interface entre o ar e um material deste tipo iremos ter dois ângulos de
refração, isto é, o feixe divide-se em dois, que se propagam no interior
do meio com direções e velocidades diferentes. No caso de incidência
normal, não há separação entre os dois feixes mas, devido à diferença de
velocidades, vai existir uma diferença de fase entre os dois. Esta
diferença de fase permite criar dispositivos que alteram o estado de
polarização do feixe, por exemplo, rodando a direção de polarização
retilínea ou transformando a polarização linear em circular. Nestes
meios podem ocorrer fenómenos ainda mais “estranhos”, tais como a
direção em que se propaga a energia não ser coincidente com a direção em
que se propaga a fase da onda, mas não vamos abordar este tópico aqui.
Índice de refração negativo
Não
poderia terminar este texto sem falar da demonstração já efetuada com
micro-ondas da existência de índice de refração negativo9. As
implicações da existência de um índice de refração negativo fazem
qualquer professor pensar imediatamente na lei de Snell. Para onde vai o
raio refratado? Aplicando a lei verificamos que o ângulo de refração
deverá ser negativo, isto é, o raio refratado fica do mesmo lado do
incidente em relação à normal (figura 3)! Este efeito já foi demonstrado
na região das micro-ondas utilizando materiais nano-estruturados.
Existe atualmente investigação ativa no sentido de criar materiais que estendam este efeito para comprimentos de onda menores. A obtenção de materiais com índice de refração negativo no visível ainda está muito distante (implica a capacidade de estruturar os materiais a três dimensões na ordem do nanómetro) mas a aplicação destes materiais nos comprimentos de onda dos radares e nas comunicações por micro-ondas é promissora para aplicações que melhorem o seu desempenho.
A existência de índice de refração negativo põe em evidência a necessidade de clarificar qual das definições de índice de refração é que estamos a utilizar em cada situação. É claro que não vamos ter nestes materiais uma velocidade da luz negativa! Só podemos falar de índice de refração negativo quando utilizamos a segunda definição, ligada à refração entre dois meios.
Nota final
Na primeira parte deste
texto vimos as características mais clássicas do índice de refração, e
as dependências deste da frequência (dispersão) e da polarização da luz
(birrefringência), ambas intrínsecas ao material, terminando com a
novidade do índice de refração poder tomar um valor negativo para
materiais artificiais. Na segunda parte deste texto iremos abordar
dependências do índice de refração, que não são intrínsecas ao material,
e que deram origem a muitas aplicações tecnológicas.
Notas
1 O valor 1,5 está próximo do valor dos vidros mais utilizados, 1,46 a 1,56. Para aplicações específicas, a gama de vidros utilizados em ótica estende-se de 1,4 a 1,9.
2 Existe igualmente uma força magnética sobre os eletrões em movimento que também dá uma pequena contribuição. Normalmente esta contribuição é cerca de cinco ordens de grandeza inferior à contribuição do campo elétrico, só se tornando relevante quando existe alguma supressão do efeito elétrico.
3 Este espalhamento é, entre outros, responsável pela cor azul do céu e pelo laranja do pôr do sol.
4 Desde que não seja demasiadamente elevada, de forma à proximidade entre átomos alterar a resposta destes.
5 Na vizinhança das riscas de absorção poderemos ter situações em que o índice de refração aumenta com o comprimento de onda (dispersão anómala).
6 Existem alguns materiais naturais que exibem quiralidade, i.e., não sobreponibilidade entre o original e a sua imagem num espelho plano, (DNA, Sacarose, Quartzo, etc.). Estes materiais podem ser estudados considerando polarizações circulares e um índice de refração diferente para cada um dos dois estados de polarização circular (direita e esquerda). Com a incidência de luz linearmente polarizada iremos ter na saída luz polarizada linearmente mas com a sua direção de polarização rodada de um ângulo cujo valor é linearmente proporcional à concentração da substância e ao comprimento de propagação. Estes instrumentos, polarímetros, são muito utilizados para a medição da concentração de açúcar nas refinarias e engenhos de açúcar ou na determinação da maturação de um fruto.
7 De forma simplista, podemos dizer que a incerteza no tempo (duração do impulso) vezes a incerteza na sua frequência (proporcional à largura espectral) tem que ser maior, ou igual, a um.
8 A uma taxa de 5 GBit/s, teríamos impulsos com cerca de 0,1 ns de duração para transmitir os bits. Com a dispersão típica das fibras óticas teríamos, ao fim de 300 km, os impulsos alargados para mais de dez vezes a sua duração inicial. Com uma taxa de 1 GBit/s já não haveria sobreposição de impulsos ao fim desta distância.
9 Phys. Rev. Lett., 84, 4184-4187 (2000); Science, 292, 77-79 (2001). Um texto bastante bom sobre o assunto pode ser encontrado na Wikipédia
Referências
- 1 Phys. Rev. Lett., 84, 4184-4187 (2000)
- 2 Science, 292, 77-79 (2001)
Este artigo já foi visualizado 5080 vezes.



