Clique aqui para aceder à 1.ª parte do artigo.

Dependência da temperatura

A temperatura, através da agitação dos átomos e moléculas, altera o espetro de absorção do material, afetando assim a velocidade de propagação da luz. O cálculo a priori desta dependência é bastante complexo, havendo vidros cujo índice de refração aumenta com a temperatura a um comprimento de onda, diminuindo noutro comprimento de onda¹.

Dependência das tensões mecânicas

Como vimos, assimetrias na distribuição dos átomos, ou moléculas, num corpo podem dar origem a birrefringência. Um caso particular ocorre quando aplicamos uma força, ou melhor, uma tensão mecânica sobre um objeto transparente e isotrópico. A aplicação da tensão vai originar, a nível microscópio, alguma alteração das distâncias atómicas (fenómeno semelhante ao que acontece num fio condutor, em que a aplicação de uma tensão mecânica altera a sua resistência elétrica) e, por isso, a resposta atómica ao campo elétrico da luz passa a ser assimétrica, originando birrefringência.

Este efeito é, por vezes, utilizado para detetar rapidamente pontos de grande tensão mecânica em peças especiais observando modelos transparentes sob tensão entre polarizadores cruzados (figura 1).

Muitos objetos de vidro e plástico têm tensões mecânicas internas originadas pelo arrefecimento rápido aquando da sua produção. Por esta razão os espelhos e lentes utilizados em telescópios são arrefecidos muito lentamente para reduzir ao máximo estas tensões internas.

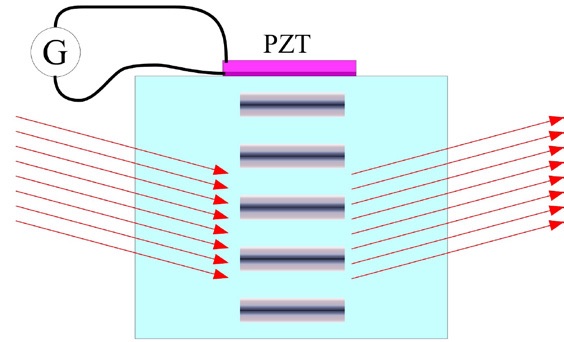
tensão mecânica constitui o domínio da Acusto-Ótica, onde a luz é controlada por ondas acústicas. Uma onda acústica (longitudinal, ou transversal), ao atravessar um meio transparente, altera o índice de refração de forma periódica, criando uma rede de difração. Esta, por sua vez difrata parte da luz que atravessa o material (figura 2). Atualmente estes dispositivos podem ter eficiências bem acima de 90% e são utilizados para fazer varrimento de um feixe laser sobre uma superfície, ou para obter impulsos Q-Switched ou Mode-Locked em lasers.

Dependência do campo elétrico

aplicação de um campo elétrico a um material altera a distribuição da nuvem eletrónica dos átomos, dando origem a uma alteração da frequência natural de oscilação desta, sendo diferente para as três direções. Esta alteração da frequência natural de oscilação (ou frequência em que o material absorve) dá origem a uma alteração do índice de refração diferente para cada orientação do campo elétrico da luz relativamente ao campo aplicado ao material, criando, ou alterando, a birrefringência. Estes efeitos eletroóticos são designados por Efeitos Pockels², presente apenas em materiais sem centro de simetria, e por Efeito Kerr³, presente em todos os materiais.

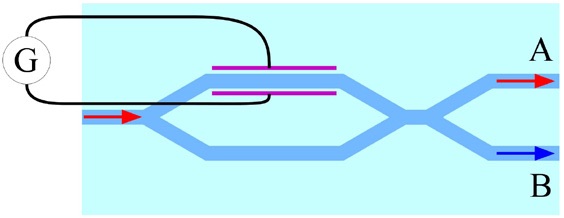
Esta birrefringência pode ser utilizada por muitas aplicações tecnológicas, de entre as quais salientamos os ecrãs de cristais líquidos, em que a rotação de moléculas por aplicação de um pequeno campo elétrico permite alterar suficientemente a polarização da luz para ser bloqueada por um polarizador. Outra aplicação muito generalizada é a de modulação da luz na transmissão de informação em fibra ótica, através da alteração da fase num braço de um interferómetro miniaturizado (figura 3).

Dependência do campo magnético

Tal como com o campo elétrico, a presença de um campo magnético altera a propagação da luz. Como só há ação de um campo magnético sobre uma carga se esta estiver em movimento, traduzindo-se por uma força perpendicular ao campo e ao vetor velocidade, é de esperar que o comportamento da luz tenha agora algumas particularidades surpreendentes. A birrefringência criada por um campo magnético é uma birrefringência circular.

Esta birrefringência, de forma simplista, causa a rotação da direção da polarização linear da luz com a propagação. No entanto, este efeito (Efeito Faraday⁴) tem uma característica que o distingue da atividade ótica presente em materiais oticamente ativos (como o quartzo e a sacarose), que consiste em o efeito não ser recíproco. Nos meios oticamente ativos, a direção da polarização linear roda com a propagação de forma recíproca, isto é, se invertermos o sentido de propagação da luz, roda agora em sentido contrário. Se colocarmos um espelho no final do trajeto, de forma a refazer o caminho em sentido contrário, obtemos o mesmo estado de polarização que na entrada. No efeito Faraday, a rotação da direção de polarização mantém-se no mesmo sentido quando invertemos o sentido de propagação, isto é, se colocarmos um espelho no final do material, obtemos no início uma rotação dupla do que teríamos no trajeto só de ida.

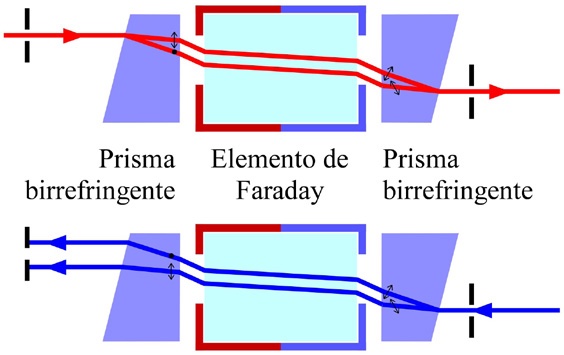
Este efeito tem aplicações óbvias na tecnologia, quando pretendemos ter algum efeito não recíproco. Uma aplicação generalizada é a proteção de díodos laser contra retrorreflexões⁵ através dos chamados “isoladores óticos” (figura 4).

Dependência da intensidade luminosa

Para finalizar esta listagem de efeitos sobre o índice de refração, vamos abordar a sua dependência da intensidade luminosa. Tal como na propagação do som no ar, a velocidade da luz num meio transparente também se altera com a amplitude da onda. Este efeito, designado como Efeito Kerr Ótico, é muito diminuto⁶ , pelo que só se torna observável para irradiâncias elevadas, ou para longas distâncias de propagação. Nas fibras óticas, dada a elevada distância de transmissão, este efeito torna-se importante e impõe um limite à potência máxima que pode ser injetada na fibra, com consequências na máxima distância de transmissão.

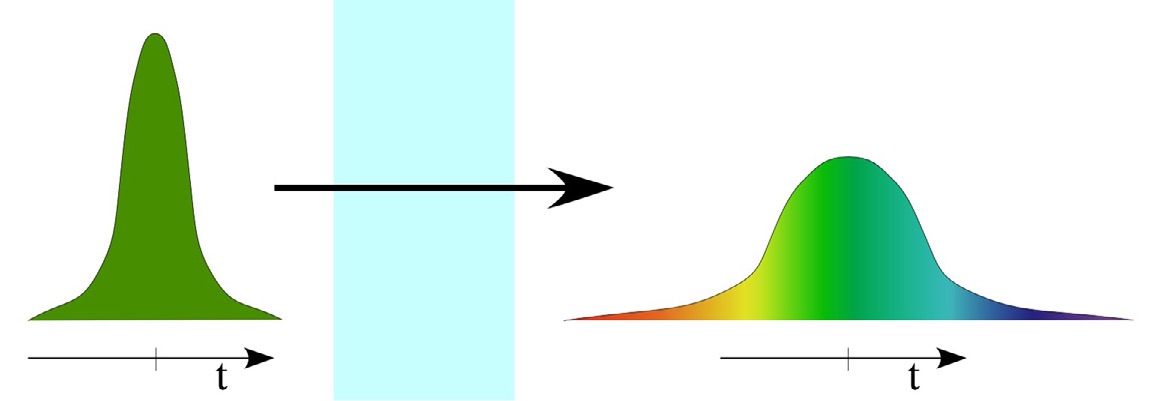
Na passagem de um impulso luminoso através de um meio em que este efeito seja relevante, e positivo, vamos ter um aumento do índice de refração à medida que a intensidade cresce, e uma diminuição do índice no flanco descendente. O aumento do índice durante a parte ascendente do impulso é equivalente a considerarmos que a fonte luminosa se está a afastar, assim, teremos uma alteração da frequência da luz no sentido do vermelho no início do impulso (figura 5). Pelo mesmo raciocínio, iremos ter uma deslocação para o azul no flanco descendente. Por este mecanismo, criam-se novas frequências dentro do impulso, alargando o seu espectro. Como, na dispersão normal, as frequências mais baixas viajam mais depressa do que as frequências mais altas, este mecanismo vai alargar mais rapidamente o impulso do que no caso da potência injetada ser menor. Por outro lado, o facto de a alteração do índice poder ser sentida por outros sinais a propagarem-se na fibra, limita a potência usada na multiplexagem em comprimento de onda.

As potencialidades tecnológicas deste efeito são, no entanto, muito interessantes e têm vindo a ser aplicadas. Por exemplo, é possível defletir um feixe pela presença de outro feixe; é possível criar uma lente pela passagem de um feixe laser e ao mesmo tempo alargar o seu espectro (este efeito é utilizado na geração controlada de impulsos laser com duração inferior a 10 fs). Na transmissão por fibra ótica, podem-se obter os chamados solitões óticos, pelo balanço entre a criação de novas frequências e a dispersão anómala possível em certos comprimentos de onda. A transmissão de informação através de solitões tem um grande interesse económico, dada a possibilidade de eliminar os regeneradores de sinal nas comunicações intercontinentais.

Notas finais

Espero que, com estes dois textos, os leitores tenham apreciado a riqueza das interações na Física, bem como a sua complexidade. Temos, por um lado, as propriedades de conjunto (temperatura, tensões mecânicas, etc.); por outro lado, a visão atómica, com a resposta de cada átomo individual e a sua dependência na vizinhança e campos externos, e finalmente, a interação entre estes fatores, com a referência às aplicações tecnológicas que advêm da exploração destas interações. Tudo isto aplicado a uma única grandeza, o índice de refração.

Notas

¹ Ver por exemplo a tabela em https://lightmachinery.com/ media/1552/schott_tie-19_temperature_coefficient_of_refractive_index.pdf.

² Em homenagem a Friedrich Pockels que estudou o efeito em 1893. A variação do índice é proporcional ao campo elétrico.

³ Em homenagem a John Kerr que descobriu o efeito em 1877. A variação do índice é proporcional ao quadrado do campo elétrico.

⁴ Descoberto por Michael Faraday em 1845.

⁵ Na vizinhança das riscas de absorção poderemos ter situações em que o índice de refração aumenta com o comprimento de onda (dispersão anómala). Os díodos laser trabalham muitas vezes perto do seu limiar de dano. A reintrodução de parte da sua radiação dentro da cavidade laser poderia causar instabilidades que fizessem a intensidade dentro da cavidade laser ultrapassar o limiar de dano do semicondutor provocando a sua destruição.

⁶ Tipicamente da ordem de 10^-20 m² W^-1 para a maioria dos vidros.