Comecemos por esclarecer o que entendemos por simetria de uma figura: trata-se de uma transformação que preserva distâncias (diz-se uma isometria) e que envia a figura exatamente sobre si própria: não deve ser possível distinguir a imagem inicial da final. Como exemplo, notemos que uma rotação de 90° em torno do centro da figura 1 não é uma sua simetria: a imagem final não coincide com a inicial (Fig 2). Mas uma rotação de 60° (ou de 180°), com o mesmo centro, já é uma simetria da figura 1...

Encontrámos simetrias de rotação na figura 1. Que outros tipos de simetrias existem? Naquela mesma figura, há também simetrias de reflexão (em seis retas diferentes). E, em geral e para figuras no plano, há ainda mais dois tipos de simetria, além dos dois já referidos: simetrias de translação e de reflexão deslizante.

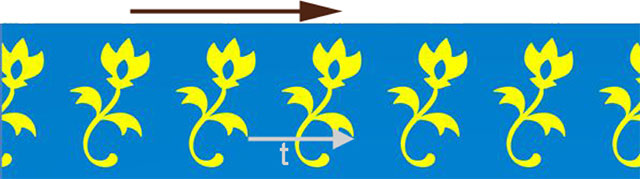
Iremos centrar-nos em três tipos de objetos no plano: rosáceas, frisos e padrões. Num friso, há simetrias de translação e, entre elas, há sempre uma “mínima” t (Fig 3): todas as outras são múltiplas de t. Num padrão há sempre duas simetrias de translação em direções diferentes (por exemplo, as translações associadas aos vetores a cinzento claro na Fig. 4), tais que qualquer outra simetria de translação se pode obter a partir daquelas duas: na figura, o vetor a castanho é a soma do vertical com o dobro do horizontal.

Algo que poderá ser surpreendente é o facto de, na imensa variedade de padrões e frisos, só existir um número relativamente pequeno de “esquemas” de simetria (grupos de simetria): 7 para os frisos e 17 para os padrões. Para as rosáceas, em que só há rotações (com uma mínima) e, eventualmente, reflexões, essa variedade de “esquemas” é infinita, contudo podemos dividir as rosáceas em dois tipos distintos: as que têm simetria de reflexão e de rotação – diedrais (Fig 1) – e as que têm apenas simetria de rotação – cíclicas (Fig 5). O Atractor1 construiu uma ferramenta relacionada com a Simetria – o programa GeCla (uma abreviatura de “Gerador e Classificador”) – que permite classificar figuras planas do ponto de vista da simetria e contém um gerador para padrões, frisos e rosáceas. O GeCla possibilita ainda uma utilização lúdica, através da realização de competições (inclusive via Internet) entre alunos de diferentes graus de ensino. O GeCla tem versões de Windows e MacOS, e o instalador pode ser importado gratuitamente a partir de www.atractor/mat/GeCla.

Este programa permite:

• Procurar simetrias. A título de exemplo, refira-se que a rosácea da Figura 7 possui 8 simetrias: 4 simetrias de reflexão, nas retas a branco, e 4 simetrias de rotação: de 0° (a identidade), de 90° (em ambos os sentidos) e de 180°.

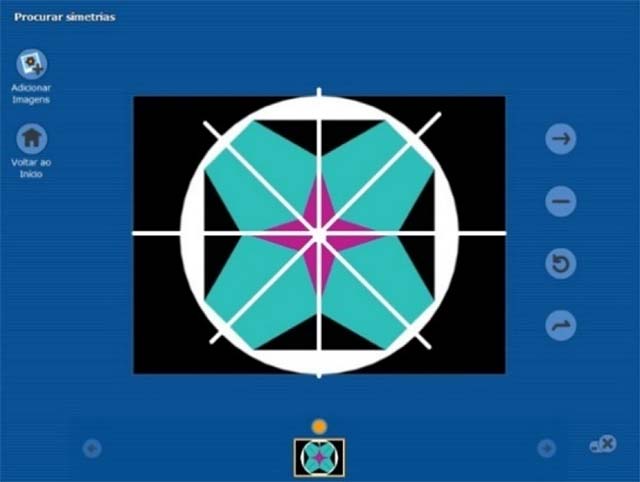
• Classificar figuras quanto ao tipo de simetria. Se tiver escolhido o modo “Com ajuda”, o utilizador será avisado dos seus eventuais erros em tempo real.

• Gerar rosáceas, frisos e padrões. Com esta ferramenta, o utilizador pode:

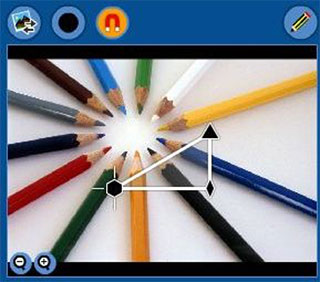
• escolher o motivo para a rosácea, friso ou padrão que pretende gerar, a partir de uma das imagens existentes (Fig 8) ou de uma foto pessoal.
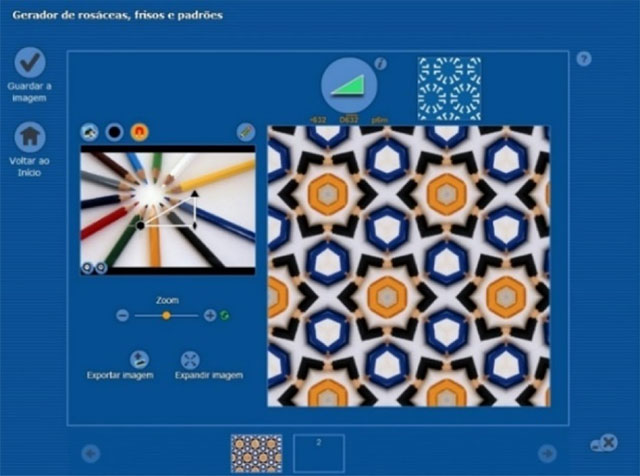
• selecionar o tipo de simetria pretendido. Para isso, deve escolher um dos 26 carimbos disponíveis no GeCla (Fig 9). Cada um destes carimbos está associado a um tipo de simetria diferente, permitindo carimbar a rosácea, o friso ou o padrão pretendidos. A título de exemplo, eis dois carimbos associados, respetivamente, a um friso e a uma rosácea: um cilindro qualquer (fig 10) e um triângulo isósceles com os lados iguais espelhados e fazendo entre eles um ângulo de 360°/6 (fig 11). Escolhamos agora como motivo uma fotografia de vários lápis (Fig 8) e como carimbo (destacado a fundo laranja na Fig 9) um triângulo retângulo (30°, 60°) com “espelhos” nos três lados; o GeCla gera o padrão patente na Figura 12. E, no ficheiro da imagem deste padrão, o programa grava também informação completa sobre as simetrias do padrão.

Um dos aspetos interessantes do GeCla é permitir a realização de competições entre duas equipas. O jogo consiste, para cada equipa:

1. na geração de imagens (o número de imagens e os tipos possíveis de simetria são definidos no início do jogo);
2. na classificação das imagens realizadas pela equipa adversária.

No final, o programa atribui uma pontuação e indica, para cada imagem, o primeiro erro cometido, caso a classificação não esteja correta.

Uma primeira competição internacional Portugal – Itália teve já lugar e o Atractor está disponível para colaborar com escolas que pretendam promover competições entre alunos de diferentes graus de ensino, quer de uma mesma escola quer de escolas diferentes. Eventuais professores interessados na realização de competições podem solicitar apoio do Atractor através do email atractor@atractor.pt.

Para alunos mais novos, por exemplo do 1º ciclo, o Atractor concebeu uma outra versão do GeCla, o GeCla Mini (que é instalado em simultâneo com o GeCla).

Notas

¹ A Associação Atractor é uma Associação sem fins lucrativos cujo objetivo principal é atrair o público para a Matemática (www.atractor.pt).