A figura 1 mostra uma circunferência de raio 1, e um polígono regular inscrito com $n$ lados (na figura $n = 5$). $s_{n} = AB =$ comprimento de um lado desse polígono. D bisseta o arco AB e portanto $s_{2n} = AD = DB =$ comprimento de um lado de um polígono regular inscrito com $2n$ lados.

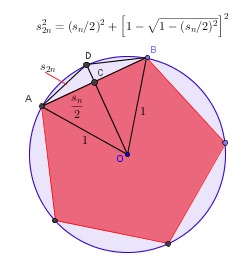
Aplicando o teorema de Pitágoras ao triângulo ACD, retângulo em C, obtemos

$s_{2n}^2=AD^2=AC^2+CD^2=AC^2+(OD-OC)^2=\left(\displaystyle \frac{s_n}{2}\right)^2+(1-OC)^2$

Uma segunda aplicação do teorema de Pitágoras, desta vez ao triângulo ACO, retângulo em C, dá

$OC=\sqrt{OA^2-AC^2}= \sqrt{1- \left(\displaystyle \frac{s_n}{2}\right)^2}$

Substituindo na primeira equação e fazendo alguns cálculos simples obtemos então (verifique)

$s_{2n}=\sqrt{2-\sqrt{4-s_n^2}}$

o que nos permite calcular $s_{2n}$ à custa de $s_{n}$.

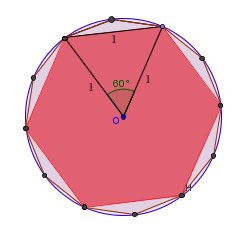
Se agora fizermos $n = 6$ (um hexágono regular inscrito), sabemos que $s_{6} = 1$ (figura 2). Aplicando sucessivamente a fórmula anterior, e após alguns cálculos simples, vem que

$$\begin{eqnarray*} s_{12} &=& \sqrt{2-\sqrt{3}}\nonumber\\ s_{24} &=& \sqrt{2-\sqrt{2+\sqrt{3}}}\nonumber\\ s_{48} &=& \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\nonumber\\ s_{96} &=& \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}\nonumber \end{eqnarray*}$$

e assim sucessivamente.

O perímetro de um polígono regular de 96 lados, inscrito numa circunferência de raio 1, é pois igual a $96 \times s_{96}$ o que dá uma boa aproximação do perímetro dessa circunferência. Como

$\pi=\displaystyle \frac{\mbox{perímetro de uma circunferência}}{\mbox{diâmetro dessa circunferência}}$

obtemos a seguinte aproximação de $\pi$

$\pi\approx 48 \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}\approx 3.14103 \approx 3\displaystyle \frac{10}{71}$

Arquimedes repetiu o mesmo argumento, agora para uma sequência de polígonos regulares circunscritos de 6, 12, 24, 48 e 96 lados. O leitor poderá deduzir a fórmula seguinte (veja a figura 3 e as notações lá usadas):

$S_{2n}=\displaystyle \frac{2\sqrt{4+S_n^2}-4}{S_n} \ \ \ \ \ \ \ \ (*)$

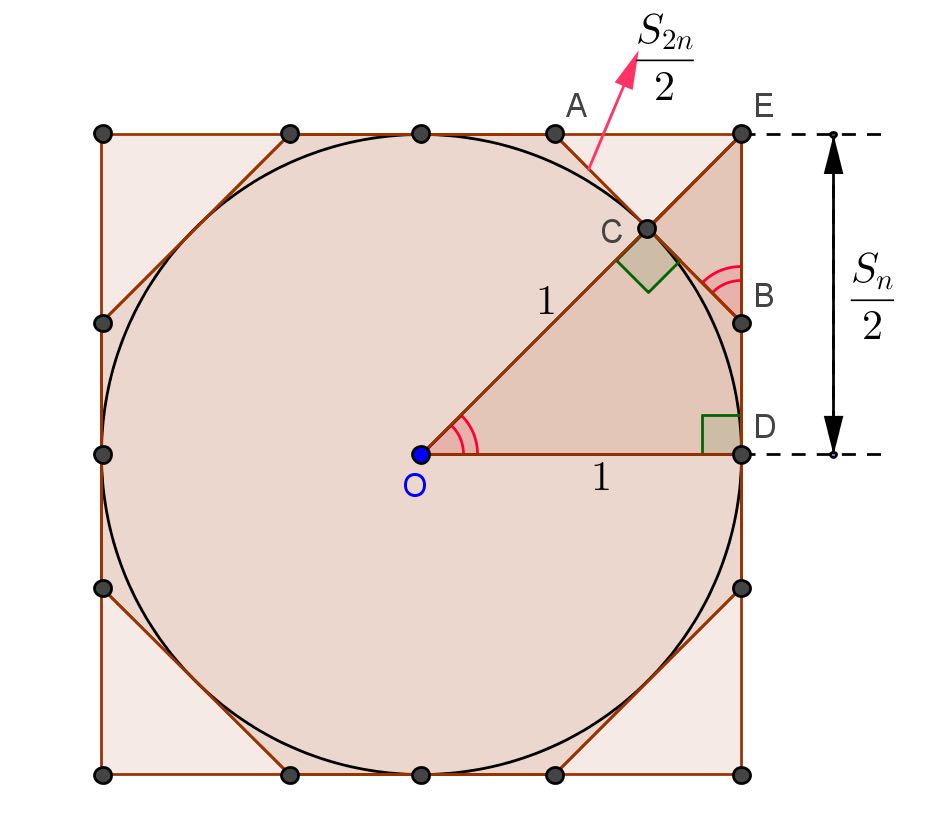
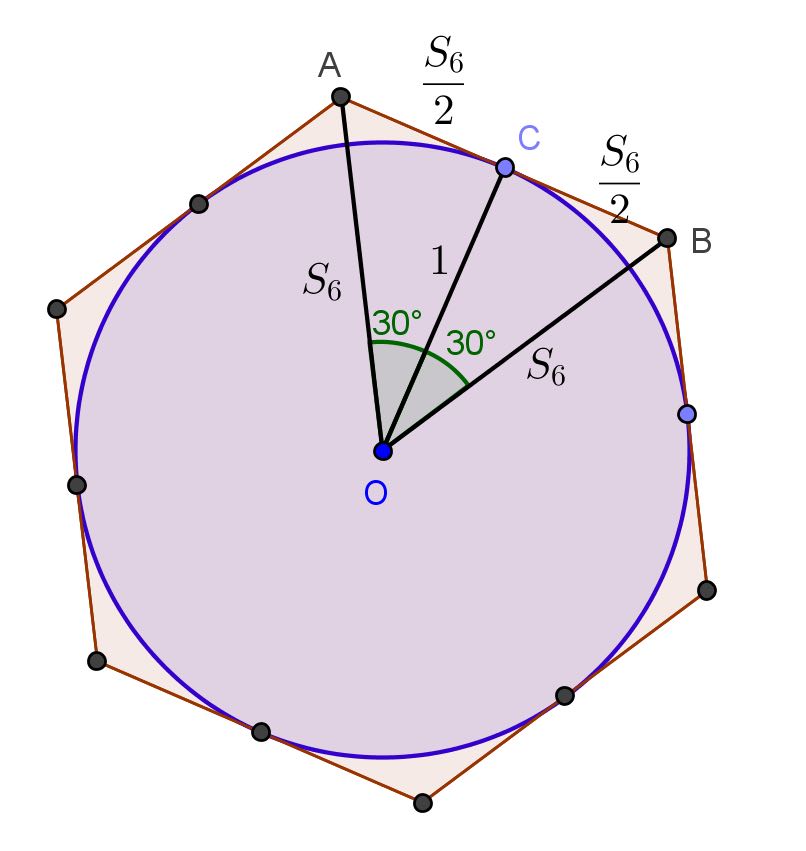
Arquimedes começa mais uma vez com um hexágono, mas desta vez circunscrito (como na figura 4). Deduz então que $S_6=2 \sqrt{3}/3$ e, usando a fórmula de recorrência (*), obtém os valores de $S_{12}$, $S_{24}$, $S_{48}$ e, finalmente, $S_{96}$. Por aproximação, calcula então o perímetro de um polígono regular de 96 lados circunscrito à circunferência de raio 1, igual a $96\times S_{96}$ e, finalmente, dividindo esse perímetro por 2 (= ao diâmetro da circunferência de raio 1), obtém o valor aproximado de $\pi$ (por excesso):

$\pi\approx 3.14271\approx \displaystyle3\frac{1}{7}$