Considere-se um espaço de resultados S e uma probabilidade P nesse espaço. Dados dois acontecimentos A e B, com P(B) > 0, define-se probabilidade condicional de A se B (ou dado B, ou sabendo B, ou condicional à ocorrência de B), e representa-se por P(A | B), como sendo

$P(A|B)=\frac{P(A \cap B)}{P(B)}$

Mais concretamente, ao falarmos na probabilidade condicional, nomeadamente probabilidade do acontecimento $A$ dado $B$, estamos a restringir o espaço de resultados em que estamos a trabalhar ao definido pelo acontecimento $B$. Assim, a probabilidade de A em B é calculada dividindo a probabilidade da interseção de $A$ com $B$, pela probabilidade de $B$.

Por exemplo, se considerarmos uma família com dois filhos, admitindo que existe igual probabilidade de ser rapaz ( $M$ ) ou rapariga ( $F$ ), o espaço de resultados associado ao fenómeno que consiste em averiguar o sexo dos dois filhos é $S = \left\{MM, MF, FM, FF\right\}$, com resultados igualmente prováveis, pelo que a probabilidade de que ambos os filhos sejam rapazes é $P\left(MM\right)=1/4$. No entanto se pretendermos a probabilidade de ambos os filhos serem rapazes, sabendo que um deles é rapaz, este condicionamento provoca que o espaço de resultados se reduza a $S' = \left\{MM, MF, FM\right\}$, donde a probabilidade pretendida será $P\left(MM\right)=1/3$. A situação descrita anteriormente pode ser representada com o seguinte diagrama de Venn

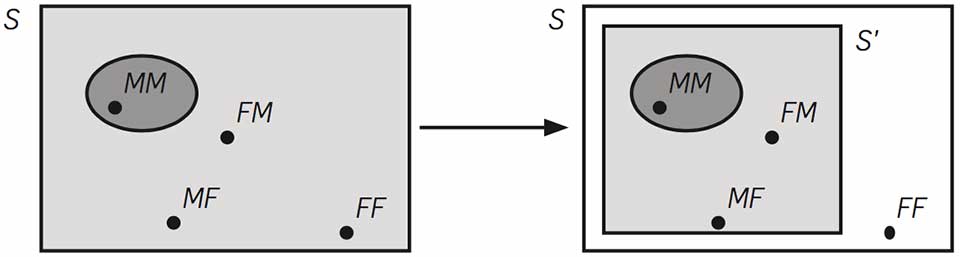
A definição de probabilidade condicional é muito útil, quando utilizada no sentido inverso, para calcular a probabilidade conjunta ou probabilidade da interseção de dois acontecimentos

$p\left(A \cap B\right) = P\left(A | B \right)P\left(B\right)= P\left(B | A \right)P\left(A\right)$

É uma noção, em geral intuitiva, quando é aplicada no cálculo de probabilidades de cadeias de acontecimentos. Por exemplo, considere-se uma turma constituída por 8 rapazes e 14 raparigas, em que se pretende selecionar uma comissão de curso constituída por 2 alunos. Pretende-se que esta seleção seja aleatória, pelo que os nomes dos alunos são escritos em 22 pedaços de papel, que se colocam num saco, de onde se extraem 2 desses papéis, ao acaso. Qual a probabilidade da comissão de curso ser constituída por dois rapazes? Se representarmos por $M_{1}$ o acontecimento “saída de um nome de rapaz na primeira extração” e por $M_{2}$ o acontecimento “saída de um nome de rapaz na segunda extração”, pretende-se a probabilidade da interseção destes acontecimentos, ou seja, $P\left( M_{1} \cap M_{2} \right)$. Tendo em consideração a definição de probabilidade conjunta, vem

$P\left( M_{1} \cap M_{2} \right)=P\left( M_{1} \right)P\left( M_{2} | M_{1} \right)=\frac{8}{22}\frac{7}{21}$

E se se pretendesse a probabilidade de numa nova seleção sair ainda um nome de rapaz? Neste caso teríamos

$P\left( M_{1} \cap M_{2} \cap M_{3} \right)=P\left( M_{1} \right)P\left( M_{2} | M_{1} \right)P\left( M_{3} | M_{1} \cap M_{2} \right)=\frac{8}{22}\frac{7}{21}\frac{6}{20}$