Cosseno de um ângulo agudo

João Nuno Tavares; Ângela Geraldo

doi:doi:10.24927/rce2017.082

João Nuno Tavares 📧 ^*, Ângela Geraldo 📧 ^ɫ

^* Faculdade de Ciências da Universidade do Porto

^{, ɫ} CMUP/ Universidade do Porto

Referência Tavares, J.N., Geraldo, A., (2017) Cosseno de um ângulo agudo, Rev. Ciência Elem., V5(4):082

Palavras-chave cosseno, seno, ângulo, triângulo

Resumo

Definição
Para definir o cosseno de um ângulo agudo de amplitude $\alpha\in ]0,90º[$ , fazemos a construção seguinte que se ilustra no applet

escolhemos um ponto qualquer C num dos lados do ângulo. Por exemplo, no applet, escolhemos o ponto C num dos lados do ângulo (no applet escolhemos o lado horizontal);
construímos a perpendicular a esse lado que passa em C;
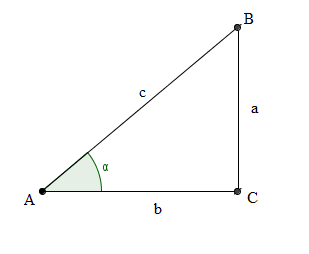
essa perpendicular intersecta o outro lado em B e, desta forma, obtemos o triângulo retângulo representado na figura - o triângulo ACB, retângulo em C.

O cosseno de $\displaystyle\alpha$ define-se agora através da razão

$\cos\alpha=\displaystyle \frac{b}{c}$

onde $b$ é o comprimento do cateto $AC$ e $c$ é o comprimento da hipotenusa $AB$ .

No applet pode escolher o valor de $\displaystyle\alpha$ com o cursor. Note ainda que o valor de $\displaystyle\cos\alpha$ não depende do ponto C escolhido no passo nº1 (pode constatar isso, variando a posição de C no applet). De facto, variando C obtemos triângulos retângulos, triângulos semelhantes entre si, e portanto a razão $\displaystyle \frac{b}{c}$ não muda.

Nota
Para qualquer ângulo agudo de amplitude $\alpha\in ]0,90º[$ , $0 < \cos\alpha < 1$ .

Valores do seno para alguns ângulos agudos:

$\displaystyle \cos \frac{\pi}{6}= \frac{\sqrt{3}}{2}$

$\displaystyle \sin \frac{\pi}{4}= \frac{\sqrt{2}}{2}$

$\displaystyle \sin \frac{\pi}{3}= \frac{1}{2}$

Ver

Relações trigonométricas num triângulo retângulo

Ciência Elementar

Cosseno de um ângulo agudo

João Nuno Tavares 📧 *, Ângela Geraldo 📧 ɫ

Resumo

João Nuno Tavares 📧 ^*, Ângela Geraldo 📧 ^ɫ