Por exemplo, no caso ilustrado no applet

\(a^2=b^2+c^2-2bc \cos\alpha\)

                     

Eis a demonstração. Considere o triângulo \(ABC\). Seja \(h\) a medida da altura relativa ao vértice \(C\) (veja o applet ao lado). O triângulo \(ADC\) é retângulo em \(D\), e daí que (teorema de Pitágoras).

\(b^2=h^2+AD^2\Longrightarrow h^2=b^2-AD^2\)

Analogamente, o triângulo \(BDC\) é retângulo em \(D\), e daí que (teorema de Pitágoras).

\(a^2=h^2+(BD)^2 \Longrightarrow h^2=a^2-BD^2=a^2-(c-AD)^2 \)

Igualando as duas expressões obtemos

\(b^2-AD^2=a^2-(c-AD)^2=a^2-c^2-AD^2+2c\, AD \)

e atendendo a que \(AD=b\cos\alpha\), vem finalmente que

\(a^2=b^2+c^2-2bc \cos\alpha\)

que é a chamada lei dos cossenos.

É importante notar que \(AD\) tem sinal positivo quando \(D\) está à direita de \(A\), e tem sinal negativo quando \(D\) está à esquerda de \(A\) (relativamente ao sentido de \(A\) para \(B\)).

Uma aplicação

Dados

  • dois círculos no plano, de raios e centros conhecidos, digamos \(\mathcal{C}_1=\mathcal{C}(z_1,R_1)\) e \(\mathcal{C}_2=\mathcal{C}(z_2,R_2)\), que não se intersectam. Portanto, usando notações complexas \(|z_1-z_2| >R_1+R_2\)
  • um terceiro círculo \(\mathcal{C}=\mathcal{C}(z,R)\) do qual apenas se conhece o raio \(R\).

Problema: calcular as posições do centro \(z\) de tal forma a que \(\mathcal{C}\) seja tangente aos dois círculos dados \(\mathcal{C}_1\) e \(\mathcal{C}_2\).

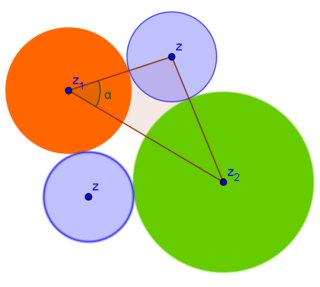
Uma aplicação da lei dos cossenos
Figura 1 - Uma aplicação da lei dos cossenos

\(z=z_1+(R+R_1)\displaystyle\frac{z_2-z_1}{|z_2-z_1|}e^{\pm i\alpha}\)

onde o ângulo \(\alpha\) é determinado pela lei dos cossenos, aplicada ao triângulo de vértices \(z_1,z_2\) e \(z\):

\(a^2=b^2+c^2-2bc \cos\alpha\)

onde

\(a=R+R_2, \ \ \ b=R+R_1, \ \ c=|z_2-z_1|\)