O modelo mais simples para descrever as rotações moleculares é o modelo do rotor rígido diatómico: dois átomos de massa m₁ e m₂, separados por uma distância fixa R (FIGURA 1A).

Por resolução da equação de Schrödinger para este modelo, obtém-se a expressão da energia dos níveis rotacionais

\(E_J=\frac{h^2}{8\pi^2I}J(J+1)\)                    (1)

Nesta expressão, J é o número quântico rotacional (J Є N_o, ou seja, pode tomar os valores 0, 1, 2, 3, 4, …) e I é o momento de inércia do rotor.

O momento de inércia é dado por

\(I=m_1r_1^2+m_2r_2^2\)                     (2)

onde r₁ e r₂ são as distâncias ao centro de massa (r₁ + r₂ = R). Esta expressão é equivalente a I = μ R², sendo μ a massa reduzida do rotor, \(\mu=\frac{m_1m_2}{m_1+m_2}\).

A equação (1) pode então escrever-se como

\(E_J=\frac{h^2}{8\pi^2\mu R^2}J(J+1)\)                    (3)

Esta forma salienta os dois fatores que afetam os níveis energia do rotor e são característicos de cada rotor: a massa e a distância entre massas. É possível agrupar estes fatores numa constante B, que é característica do sistema considerado. Daqui resulta uma forma simplificada da equação (3) - notar que B tem unidades de energia:

\(E_J=BJ(J+1)\)                    (4)

A equação (4) permite calcular facilmente os valores de energia de cada nível em função de J, assim como a separação energética entre os diferentes níveis, representada na FIGURA 1B.

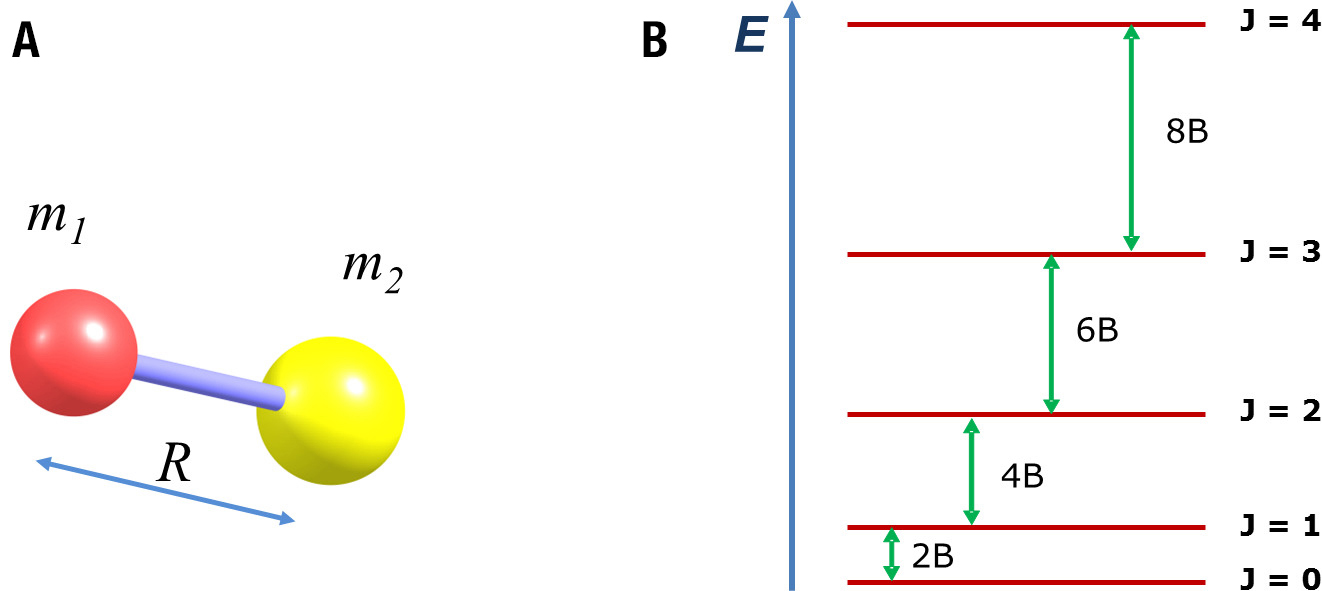
A regra de seleção para as transições rotacionais é ΔJ = ±1, ou seja, apenas são observáveis transições entre níveis consecutivos. Daqui resulta que as transições observadas correspondem a 2B, 4B, 6B,… e portanto aparecem no espectro rotacional de absorção a intervalos de valor constante, igual a 2B (FIGURA 2). Experimentalmente, a partir do valor de B, sendo conhecidas as massas dos átomos, é possível determinar com grande rigor o valor do comprimento de ligação, R.

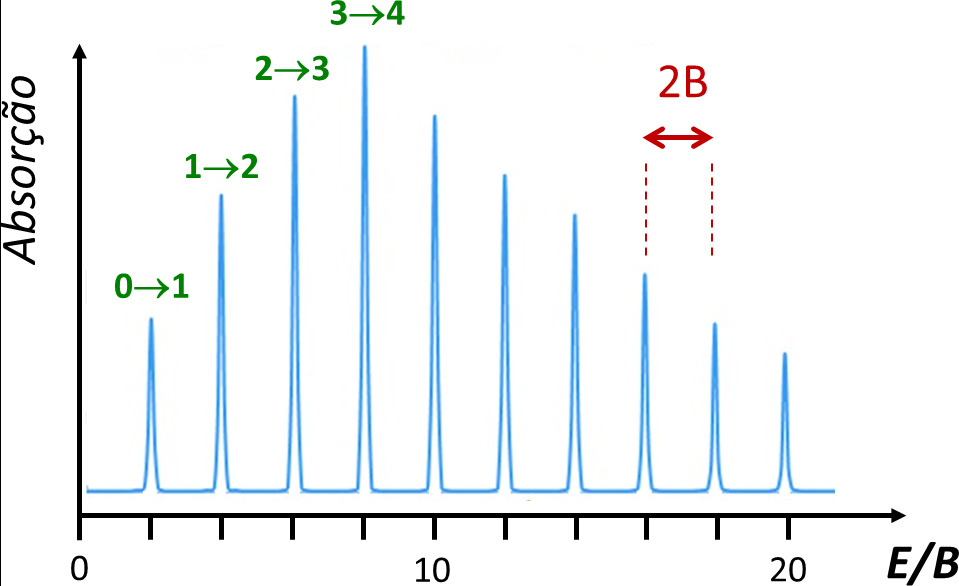
O perfil de intensidades observado na figura, com o máximo de absorção observado para a transição J=3 para J=4, merece uma explicação adicional. A intensidade de absorção depende do número de moléculas da amostra (população) que se encontra no nível de partida – no caso da FIGURA 2, o nível J=3. Com exceção do nível J=0, todos os níveis rotacionais representados na FIGURA 1A são degenerados (há mais do que um nível com a mesma energia). O grau de degenerescência de cada nível J é dado por 2J+1, o que significa que a linha inferior na FIGURA 1B representa um nível (J=0), mas a linha de J=3 representa sete níveis. Numa amostra gasosa, as moléculas distribuem-se pelos diversos níveis rotacionais disponíveis de acordo com a distribuição de população de Boltzmann, ou seja, a população é maior no nível inferior (J=0) e decresce exponencialmente com o aumento de J. No entanto, como os níveis apresentam degenerescência total crescente, numa situação em que a separação energética entre níveis é muito pequena, é possível que a totalidade da população nos sete níveis de J=3 seja superior à população do nível único J=0. A intensidade máxima de absorção corresponde ao valor de J para o qual o aumento do número de níveis degenerados ainda ultrapassa a diminuição de população nos níveis por aumento da energia.

Esta abordagem de “rotor rígido” permite interpretar os espectros rotacionais sem ter em consideração a constituição do sistema em termos de átomos e ligações químicas: na verdade, apenas interessam os momentos de inércia do sistema.

Na sua maioria, as moléculas não são lineares e possuem rotação em torno de três eixos. Estes eixos – em torno dos quais a molécula roda – são designados por eixos principais de inércia e para cada um é definido um momento de inércia, I, definido de forma análoga à da equação (2).

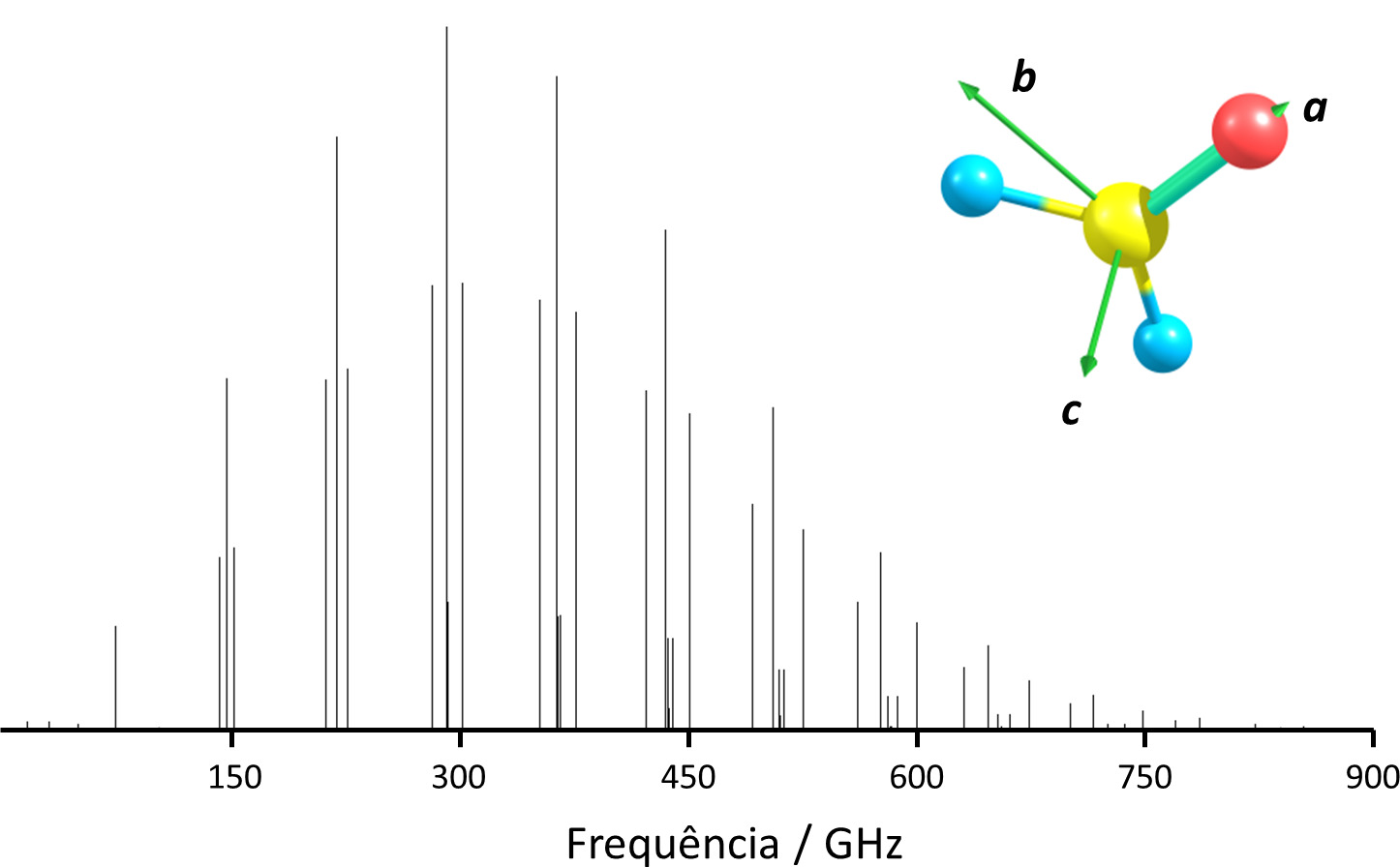
Os três momentos de inércia são designados por Ia, Ib, Ic, e os respetivos eixos a, b, c, sendo que, por convenção, o eixo a corresponde ao eixo de menor momento de inércia (Ia) e o eixo c corresponde ao eixo de maior momento de inércia (Ic). Assim, a ordem é sempre

Ic ≥ Ib ≥ Ia

As moléculas poliatómicas são então classificadas de acordo com os seus momentos de inércia, ao qual está associado um modelo de interpretação do respetivo espectro rotacional:

• Rotor linear – com um momento de inércia nulo: Ic= Ib , Ia=0.
• Rotor esférico – três momentos de inércia iguais: Ic= Ib = Ia.
• Rotor simétrico – dois momentos de inércia iguais: Ic= Ib ≠ Ia.
• Rotor simétrico – dois momentos de inércia iguais: Ic= Ib ≠ Ia.

No caso do rotor simétrico, a forma da molécula pode ainda ser “ao alto” (no inglês, prolate) ou “ao baixo” (no inglês, oblate, sendo que neste caso Ic ≠ Ib = Ia). Exemplos destes dois tipos de moléculas são o clorometano e o benzeno, respetivamente.

Os rotores reais não são rígidos, já que a ligação química é deformável. Uma das consequências deste facto é que o aumento da frequência de rotação provoca uma distorção no valor de R devido ao aumento da força centrífuga. Este efeito é contabilizado através da constante de distorção centrífuga, D, na definição da energia dos níveis rotacionais do rotor diatómico

\(E_J=BJ(J+1)-DJ^2(J+1)^2\)                    (5)

O valor de D é baixo para ligações pouco deformáveis e elevado para ligações muito deformáveis – o que permite obter experimentalmente informação acerca da rigidez de uma ligação química.

A descrição do espectro rotacional de moléculas poliatómicas não lineares tem de incluir não apenas os diferentes momentos de inércia mas também as diferentes constantes de distorção centrífuga associadas a cada eixo de inércia – o que aumenta significativamente a complexidade do problema, que será objeto de um texto mais específico (exemplo, FIGURA 3).