Neste artigo introdutório, começaremos por apresentar um exemplo simples - a corda vibrante - para, depois o generalizar e apresentar algumas das suas consequências mais importantes.

A corda vibrante

Considere-se um fio metálico esticado, preso nas suas extremidades, de comprimento a. Estando esticado, cada ponto do fio está submetido a uma tensão τ, a força que a parte do fio à direita do ponto exerce sobre a parte à sua esquerda. É conveniente tomar o eixo x coincidente com o fio, origem na extremidade esquerda do mesmo. Agora, definimos o eixo y vertical, perpendicular ao anterior, com origem comum (ver FIGURA 1). O fio pode ser afastado desta configuração de referência adquirindo, então, uma nova configuração y(x,t) a qual irá evoluir no tempo. Esta função é o campo escalar que iremos agora considerar em detalhe. Para simplificar a análise, admitimos que o afastamento é pequeno, condição traduzida na relação \(\mid\frac{\partial y}{\partial x}\mid \ll 1\). Iremos, então, ignorar termos quadráticos, ou superiores, nesta quantidade.

Cada porção do fio tem massa e está submetida a forças, umas de origem interna, como a tensão do fio, outras externas, como o seu peso ou outras forças aplicadas.

Cada porção do fio tem massa e está submetida a forças, umas de origem interna, como a tensão do fio, outras externas, como o seu peso ou outras forças aplicadas.

Prestemos atenção à porção do fio cujos pontos têm abcissas em [x, x + δx] . Após a deformação, os extremos deste intervalo adquirem ordenadas, respetivamente , y(x) e y(x+dx); nestas extremidades atua a tensão do fio exercidas pelas partes adjacentes do fio mas exteriores àquele intervalo. Essas forças são tangentes ao fio em cada um dos extremos daquele intervalo (ver FIGURA 2).

Ora, a tangente unitária num ponto genérico tem as componentes \((1,\frac{\partial y}{\partial x})\), desprezando-se aqui termos quadráticos nesta derivada, como foi assumido. Assim, na extremidade direita, a força exercida é \(\tau(1,(\frac{\partial y}{\partial x})_{x+\delta x})\), enquanto na extremidade esquerda a força exercida é \(-\tau(1,(\frac{\partial y}{\partial x})_{x})\), com o sinal negativo porque é exercida pela parte à esquerda do ponto sobre a parte à sua direita. Deste modo, a resultante destas duas forças é \(\tau(0,\frac{\partial ^2}{\partial x^2}y)\delta x\), i.e., uma força vertical dirigida para baixo (cima) onde a curvatura for negativa (positiva). Qual a massa da porção considerada? É, evidentemente, a mesma que existia antes da deformação.

Obtemos, assim, a equação das cordas vibrantes:

\(\rho \frac{\partial ^2}{\partial t^2}y=\tau\frac{\partial ^2}{\partial x^2}y + f(x,t)\)                     (1)

Vários aspetos importantes devem já ser realçados.

   1° - É uma equação linear pelo que obedece ao princípio da sobreposição: a soma algébrica de duas soluções, ainda é uma solução.

   2° - Qualquer solução tem de satisfazer às condições fronteira:

   y(0,t)=y(a,t)=0                    (2)

Estas condições correspondem aqui à exigência de estarem fixos os extremos da corda.

   3° - A solução fica completamente definida com as condições iniciais:

y(x,0)=y₀(x)

\((\frac{\partial y(x,t)}{\partial t})_{t=0}=\nu0(x)\)                     (3)

Aqui, os segundos membros são supostos conhecidos para cada problema. Deve ser claro que estes dados têm de ser compatíveis com as condições fronteira. e.g. y₀(0)=y₀(a)=0 e v₀(0)= v₀(a)=0. Notar-se-á o paralelismo com os mais habituais problemas de Mecânica onde é necessário especificar a posição e velocidade iniciais para definir integralmente uma solução.

Um exemplo simples é o caso do peso para o qual f(x)= -ρg. Em tal caso, é imediato obter uma solução particular, independente do tempo e obedecendo à equação:

\(\tau\frac{\partial ^2}{\partial x^2}y-\rho g=0\)

A solução obedecendo às condições fronteira é:

\(Y(x)=-\frac{\rho g}{2\tau}(a-x)x\)

É um arco de parábola - se não tivéssemos efetuado as aproximações indicadas, iriamos obter a bem conhecida catenária da qual a parábola é uma aproximação para pequenos deslocamentos. Na expressão acima, o mínimo da função dá-nos a flecha, i.e., o maior deslocamento, o qual apresenta, pois, o valor \(\frac{\rho ga^2}{8\tau}\), situando-se a meio do segmento. Como podemos somar esta solução a qualquer outra solução da eq. (1), iremos doravante ignorar o peso, passando a estudar, inicialmente, a solução homogénea , i.e., para f = 0 da eq. (1) que reescreveremos sob a forma:

\(\frac{\partial ^2y}{\partial t^2}=c^2\frac{\partial ^2y}{\partial x^2}\)                    (4)

onde:

\(c=\sqrt{\frac{\tau}{ϱ}}\)                     (5)

é uma constante com as dimensões de uma velocidade (não confundir com a velocidade da luz!).

A eq. (4) é a conhecida equação de onda a uma dimensão (espacial), uma das mais fundamentais equações da Física. Mais adiante, será considerada a sua generalização a três dimensões.

A solução geral da eq. (4) pode escrever-se sob a forma:

y(x,t) = F(t-x/c) + G(t+x/c)                    (6)

como imediatamente se verifica. Cada uma das funções neste 2° membro só tem um argumento e elas são, para já, completamente independentes. O significado físico destas funções é fácil de ser entendido. Começando pela função F, vemos que o seu argumento t-x/c se repete em t+δt-(x+δx)/c se δx=cδt. Mesmo argumento significa que a função F tem o mesmo valor em x+δx, no instante t+δt, que tinha em x no instante t. Quer dizer, este valor da função foi transportado para a direita com a velocidade c. Assim, a função F(t-x/c) representa uma onda que se propaga para a direita com a velocidade c. Raciocínio idêntico mostra que a função G(t+x/c) representa uma onda que se propaga para a esquerda com a mesma velocidade. Mas qual a forma analítica destas funções? É aqui que intervêm as condições fronteira (eqs. 3):

y(0,t)=0 ⟶ F(t) + G(t) = 0

y(a,t)=O ⟶ F(t-a/c)) + G(t+a/c) = 0

Estas equações têm de ser satisfeitas qualquer que seja t. Substituamos, então, na 2ª equação, t por t-a/c ; obtém-se:

F(t-2a/c) + G(t) = 0

Usando a 1ª equação anterior, concluímos um importante resultado:

F(t-2a/c) = F(t)

Quer dizer, a função F é periódica no tempo com o período 2a/c ; o mesmo se passa com a outra função porque G(t) = - F(t). São, pois, funções trigonométricas, mas a sua expressão mais simples apela à representação complexa. De facto, considere-se a função \(e^{in\omega_0t}\), onde \(\omega_0=\frac{\pi c}{a}\), designada por frequência fundamental, é um inteiro. Esta exponencial é periódica a com o período indicado:

\(e^{in\omega_0(t+\frac{2a}{c})}=e^{in\omega_0t}e^{in\omega_0\frac{2a}{c}}=e^{in\omega_0t}e^{in2\pi}=e^{in\omega_0t}\)

Temos assim que F(t) pode ter a forma \(e^{in\omega_0t}\) multiplicada por uma constante arbitrária. O mesmo se passa com G(t) = - F(t)= -\(e^{in\omega_0t}\). Regressando à eq. (6), vemos que devemos considerar \(F(t-x/c) = e^{in\omega_0(t-\frac{x}{c})}\) e \(G(t+x/c)= e^{in\omega_0(t+\frac{x}{c})}\). Deste modo, construímos uma solução:

\(y(x,t)=e^{in\omega_0(t-\frac{x}{c})}-e^{in\omega_0(t+\frac{x}{c})}=2i\, e^{in\omega_0t}\, sen(\frac{n\omega_0x}{c})\)

que pode ser multiplicada por uma constante arbitrária na qual se pode absorver o fator (-2i). Assim:

\(y(x,t)=C_n\, e^{in\omega_0t}\, sen(\frac{n\omega_0x}{c})\)

é solução qualquer que seja o inteiro n. Três observações são aqui pertinentes:

   1ª Vemos que n=0 está excluído porque daria a função identicamente nula.

   2ª A verdadeira solução é obtida tomando a parte real do 2° membro. Ora, mesmo que C_n seja um número complexo, para já arbitrário, as funções com n > 0 e n < 0 não são linearmente independentes na sua dependência espacial (em x). De facto, escrevendo \(C_n=\lceil c_n\rceil e ^{iα_n}\), obteríamas para a parte real da expressão acima:

\(y(x, t) = \lceil c_n\rceil cos(n\omega_0t+α_n)\, \, sen(\frac{n\omega_0x}{c})\)

Vemos agora que trocando n por -n na função anterior, obtinhamos uma função que, embora tendo uma parte temporal diferente, não é independente da anterior no que respeita à sua dependência espacial.

Deste modo, concluímos que n deve ser um inteiro positivo.

3ª Pelo princípio da sobreposição, a soma algébrica de soluções, como a encontrada atrás, ainda é solução da eq. (4). Sendo assim, a solução geral daquela equação escreve-se:

\(y(x,t)=\sum_{n+1}^{∞} C_ne^{in\omega_0t} sen(\frac{n\omega_0x}{c})\)                    (7)

recordando-se que, no fim dos cálculos, deve ser tomada a parte real do 2° membro.

Finalmente, a determinação das constantes C_n faz-se pelas condições iniciais (eqs 3). Para isso, usa-se a ortogonalidade das funções \(sen(\frac{n\omega_0x}{c})\) dentro do intervalo [0,a]. Vejamos o que isso significa. Comecemos por simplificar notações, designando por

\(k_n\equiv\frac{n\omega_0}{c}=\frac{n\pi}{a}\)

Estas quantidades são chamadas por vetores de onda (embora, aqui, o caráter vetorial esteja ausente). Ora:

\(\int_{0}^{a} dx \, \, sen(k_nx)\, \, sen(k_nx)=\begin{cases}0 \, \, \, se & n \neq m\\ \frac{a}{2} \, \, se & n \neq m\end{cases}\)                    (8)

relação conhecida por ortogonalidade daquelas funções. A relação prova-se facilmente empregando uma identidade trigonométrica:

\(\int_{0}^{a} dx \, \, sen(k_nx)\, \, sen(k_mx)=\frac{1}{2}\int_{0}^{a}dx\, [cos\, ((k_n-k_m)x)-cos\, ((k_n+k_m)x)]\)

No caso n ≠ m, a integração dá 0 porque \((k_n\mp k_m)a=(n \mp m)\pi\).

No caso n = m, a integração dá \(\frac{a}{2}\) resultando apenas da 1 ª parcela do 2° membro.

Assim, regressando à 1ª equação em (3) e multiplicando ambos os membros por sen(k_nx), tem-se:

        \(\int_{0}^{a} dx \, \, y_0(x)\, \, sen(k_nx)=\int_{0}^{a} dx \, \, y(x,0)\, \, sen(k_nx)=\)

\(Re \Bigg\{ \sum_{m=1}^∞C_m\int_{0}^{a} dx \, \, sen (k_nx) \int_{0}^{a} dx\, \, sen (k_nx)\, \, sen (k_mx)\Bigg\}=Re\Bigg\{C_n\frac{a}{2}\Bigg\}\)

Do mesmo modo, obtém-se para a 2ª equação em (3):

\(\int_{0}^{a} dx\, \, v_0(x)sen(k_nx)=\int_{0}^{a}dx\, (\frac{\partial y(x,t)}{\partial t})_{t=0}\, sen(k_nx)=Re\Bigg\{in\, \, C_n\frac{a}{2}\Bigg\}\)

Aqui, o símbolo Re indica que deve ser tomada a parte real do que se lhe segue. Como as funções y₀(x) e v₀(x) são dadas, os primeiros membros das relações anteriores são calculáveis, determinando-se, dessa forma, as constantes complexas C_n.

Exemplo: Suponhamos que v₀(x)=0, i.e., a corda é inicialmente largada com velocidade nula e na configuração representada na FIGURA 3:

\(y_0(x)=\begin{cases}\frac{\frac{y_0x}{b}}{-\frac{y_0(x-a)}{a-b}}\end{cases} \begin{array}{c}para & 0 < x < b\\ para & b < x < a\end{array}\)

O cálculo efetua-se sem dificuldade, obtendo-se:

\(C_n=\frac{2y_0}{k_n^2(a-b)b}sen(k_nb)\)

Este resultado mostra que as amplitudes \(C_n\approx\frac{1}{n^2}\) diminuem rapidamente de valor quando n aumenta, diminuindo assim a importância dos harmónicos (modos com frequência ω_n com n>1 ). Mas há outro modo de eliminar harmónicos. Por exemplo, se \(b=\frac{a}{3}\). então \(k_nb=n\frac{\pi}{3}\) e são, pois, eliminados os harmónicos n=3,6,9, .. É, assim, admirável a execução de um instrumentalista de cordas (viola, violino, violoncelo) que executa rapidamente a seleção dos harmónicos pretendidos. E se nos lembramos que tal intérprete, com a sua mão fixa, pode alterar com a pressão dos dedos o comprimento efetivo da corda, não podemos senão admirar-nos da imensa riqueza melódica que consegue extrair do seu instrumento.

O leitor, contudo, não deixará de objetar que o dedo do guitarrista ou o arco do violoncelista introduzem forças exteriores sobre a corda e que não foram consideradas na análise anterior. Retomemos, então, a eq. (1) que escreveremos sob a forma:

\(\frac{\partial ^2}{\partial t^2}y-c^2\frac{\partial^2}{\partial x^2}y=\frac{1}{\rho}f(x,t)\)                     (9)

A equação mantem-se linear e as soluções têm de continuar a obedecer às condições fronteira. O que, agora, procuramos é a solução particular determinada pela força externa, à qual se pode sempre adicionar qualquer solução da equação homogénea, como atrás se determinaram. É aqui útil utilizar a decomposição de y(x,t) no conjunto das funções ortogonais já encontradas, o que logo garante a satisfação das condições fronteira. Assim, escreveremos:

\(y(x, t) = \sum_{n=1}^∞ y_n(t)\, \, sen(k_nx)\)

Substituindo na eq. (9), vem:

\(\sum_{n=1}^∞ \left[\frac{d^2y_n}{dt^t}+\omega_n^2y_n(t)\right]\, sen(k_nx)=\frac{1}{\rho}\, \, f(x,t)\)

onde ω_n= n ω₀. Usemos, agora, a ortogonalidade das funções (eq. 8), para concluir:

\(\frac{d^2y_n}{dt^t}+\omega_n^2y_n(t)=\frac{2}{a}\int_{0}^{a}dx \, \, sen (k_nx) \frac{1}{\rho}f(x,t)\equiv\frac{f_n(t)}{\rho}\)

onde a última igualdade define as grandezas f_n(t). A linearidade desta equação permite utilizar o princípio da sobreposição: já conhecemos a solução da equação homogénea (\(C_{n} e^{iω_nt}\)), pelo que nos resta procurar uma solução particular. Suponha-se, como exemplo, que \(f_n(t)=f_ne^{i\omega t}\); obtemos:

\(y_n(t)= R_e\left[C_ne^{i\omega_n t}+\frac{f_{n}}{\rho}\frac{e^{i\omega t}}{\omega_n^2-\omega^2}\right]\)

No último termo, vemos a caraterística de uma ressonância quando ω ≈ ω_n. Para vermos o que acontece exatamente na ressonância, temos de considerar as condições iniciais: admitamos que a corda está parada na posição de referência y(x,0)=0. Neste caso, obtemos:

\(C_n=-\frac{f_n}{\rho}\frac{1}{\omega _n^2-\omega^2}\), pelo que:

            \(y_n(t)=Re\left[\frac{f_n}{\rho}\frac{e^{i\omega t}-e^{i\omega _nt}}{\omega_n^2-\omega^2}\right]\)

Fazendo ω → ω_n , vem:

\(y_n(t)=Re\left[\frac{f_n}{\rho}\frac{i\, t\, e^{i\omega_nt}}{2\omega _n}\right]\propto t\)

A amplitude do harmónico cresce no tempo, embora venha a ficar limitada pelos termos não lineares que foram ignorados. É assim que o instrumentalista musical obtem notas intensas do seu instrumento, ainda mais amplificadas pela caixa de ressonância que o integra!

Campos escalares: resultados gerais

Aqui, iremos expor vários resultados importantes para campos escalares definidos em todos os pontos do espaço e dependentes do tempo. Embora a equação de campo seja apresentada sem qualquer dedução, ela é, contudo, obtida quer exatamente quer sob aproximações justificadas, em muitas áreas da Física, da dinâmica de fluidos à acústica, do eletromagnetismo à ótica. Designando o campo escalar por \(\psi(x,y,z,t)\equiv \psi (\overrightarrow{r},t)\), admitiremos, então, que ele satisfaz à equação de onda.

\(\frac{1}{c^2}\frac{\partial ^2}{\partial t^2}\psi - Δ\psi=\sigma(\overrightarrow{r},t)\)                     (10)

Há vários aspetos a salientar.

    1° - O 2° membro é interpretado como fonte do campo. Na sua ausência, o campo diz-se livre.

    2° - A constante c tem as dimensões de uma velocidade (mais uma vez, não deve, em geral, confundir-se com a velocidade da luz), antecipando-s que seja a velocidade de propagação do campo.

    3° - O símbolo Δ representa o operador Laplaciano:

\(Δ=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}\)

Para um campo escalar, este operador obtém-se de dois outros importantes operadores:

    a) O operador gradiente¹, representado por ∇, definindo um vetor quando atua sobre ψ, nomeadamente, ∇ ψ o vetor de componentes cartesianas \( (\frac{\partial \psi}{\partial x},\frac{\partial \psi}{\partial y},\frac{\partial \psi}{\partial z})\).

    b) O operador divergência que atua sobre um campo de vetores \(\overrightarrow{v}(\overrightarrow{r},t)\):

div \(\overrightarrow{v}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}=∇\cdot \overrightarrow{v}\)

É, agora, fácil verificar a identidade: \(\Delta \psi = ∇\cdot∇\psi\).

    4° Para uma fonte estática (independente do tempo), a eq. (10) admite uma solução particular, também estática, que satisfaz à equação de Poisson:

\(\Delta \psi = -\sigma(\overrightarrow{r})\)                     (11)

A solução desta equação é bem conhecida do Eletromagnetismo:

\(\psi (\overrightarrow{r})=\frac{1}{4\pi}\int d\overrightarrow{r}'\frac{\sigma(\overrightarrow{r'})}{|\overrightarrow{r}-\overrightarrow{r'}|}\)

Regressando à eq. (10), ela deve ser complementada por duas condições:

    a) Condições iniciais, onde são dados \(\psi(\overrightarrow{r},0)\) e \( (\frac{\partial \psi(\overrightarrow{r,t})}{\partial t})_{t=0}\) em todos os pontos do espaço.

    b) Condições fronteira, onde são dados \(\psi (\overrightarrow{r},t)\) ou \(∇ \psi (\overrightarrow{r},t)\) em duas superfícies distintas e imóveis, sendo frequente que uma dessas superfícies se situe “no infinito”.

A eq. (10) lembra a lei fundamental da dinâmica se imaginarmos \(\frac{\partial ^2}{\partial t^2}\psi\) como uma aceleração e a fonte como uma força. Vamos explorar esta analogia. Para isso, consideramos uma superfície fechada Σ, de normal unitária exterior \(\overrightarrow{n}\), limitando um domínio finito D (FIGURA 4). Seguido a analogia, somos levados a definir a “quantidade de movimento” do campo, no interior desta superfície, por:

\(P(t)=\int_{D}dV\frac{\partial \psi (\overrightarrow{r},t)}{\partial t}\)                    (12)

Estudemos como P varia no tempo:

\(\frac{dP}{dt}=\int_{D}dV\frac{\partial ^2\psi(\overrightarrow{r},t)}{\partial t^2}=c^2\int_{D}dV\left[\Delta\psi(\overrightarrow{r},t)+\sigma(\overrightarrow{r},t)\right]\)

Usando o teorema de Gauss² para o 1° termo no último membro, obtemos:

\(\frac{dP}{dt}=c^2\int_{Σ} dS \overrightarrow{n}\cdot ∇ \psi + c^2 \int_{D} dV \sigma (\overrightarrow{r},t)\)

Ora, por que deve variar no tempo a “quantidade de movimento” daquele domínio? Em Mecânica, diríamos que há forças aplicadas no interior do domínio, o que nos leva a identificar \(c^2\int_{D} d\overrightarrow{r}\sigma(\overrightarrow{r},t)\) como a “quantidade de movimento” criada pelas fontes na unidade de tempo. Mas que representa o outro termo na equação anterior? Se recordarmos que um campo se propaga, então há outra maneira de fazer “crescer” a “quantidade de movimento” em D, nomeadamente, através do fluxo de “quantidade de movimento” que “entra” no domínio pela superfície (note-se a associação de “cresce” com “entra”). Se “entra” então deverá ter o sentido de \(-\overrightarrow{n}\), o que nos leva à identificação:

\(-c^2∇\psi\cdot(-\overrightarrow{n})=\) “quantidade de movimento” do campo transmitida por unidade de tempo e por unidade de área para o interior da superfície Σ.

A equação anterior exprime, então, a lei genérica de conservação da “quantidade de movimento”.

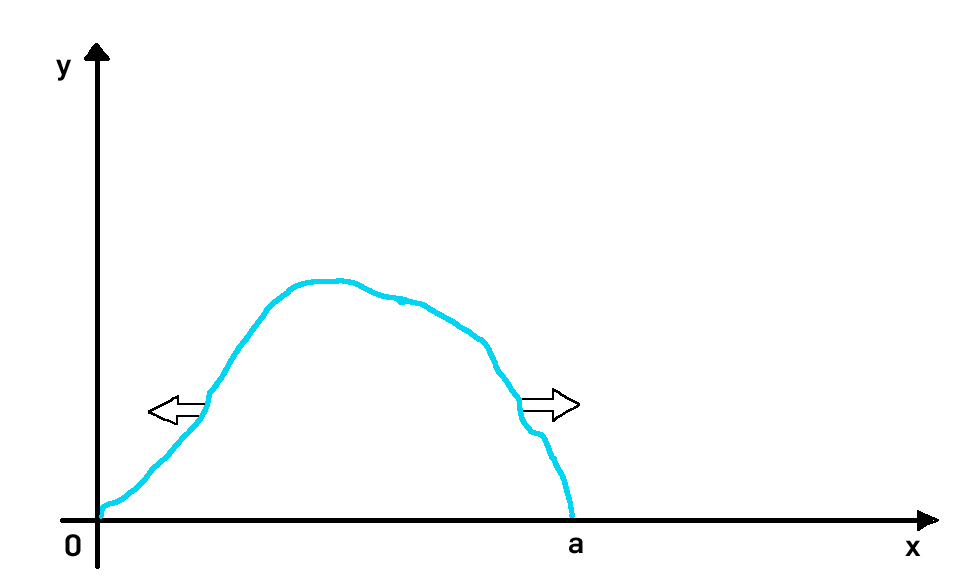
Exemplo: no caso da corda vibrante, consideremos o domínio definido pela origem e um ponto B, fixo, de abcissa b < a. A superfície Σ, aqui unidimensional, reduz-se a estes dois pontos.

Então, identificando \(\psi(x,t)\equiv \rho y (x,t)\), concluímos que \( \rho c^2 \frac{\partial \psi}{\partial x}=\tau \frac{\partial y}{\partial x}\) é o fluxo da quantidade de movimento que entra neste domínio através de B (notar que, neste ponto, \(\overrightarrow{n}\) é o versor do eixo x). Reconhecemos que é a força, devida á tensão do fio, exercida pela parte à direita de B sobre a parte à sua esquerda. Uma outra força, dada pela mesma expressão, mas com o sinal trocado, atua na origem. Note-se que a oscilação da corda dá-se na direção vertical mas o fluxo da quantidade de movimento dá-se na direção horizontal. A FIGURA 5 esquematiza (setas) o fluxo da quantidade de movimento nos pontos selecionados.

Regressando, de novo, ao campo escalar genérico e prosseguindo a analogia mecânica, será agora natural considerar a “energia cinética” no interior do mesmo domínio D atrás definido:

\(K=\frac{1}{2}\int_{D} dV (\frac{\partial \psi}{\partial t})^2\)

Como evolui no tempo esta energia? Derivando e usando a eq. (10), encontramos:

\(\frac{dK}{dt}=\int_{D} dV\frac{\partial \psi}{\partial t}\frac{\partial ^2\psi}{\partial t^2}=\int_{D}dV\frac{\partial \psi}{\partial t}\left[c^2\Delta\psi+c^2\sigma\right]\)

Ora, consideremos a identidade:

\(\frac{\partial \psi}{\partial t}\Delta\psi=\frac{\partial \psi}{\partial t}∇\cdot(\nabla\psi)=∇\cdot(\frac{\partial \psi}{\partial t}\nabla\psi)-(\frac{\partial \Delta\psi}{\partial t})\cdot\nabla\psi=\nabla\cdot(\frac{\partial \psi}{\partial t}\nabla\psi)-\frac{1}{2}\frac{\partial}{\partial t}(\nabla\psi)^2\)

Substituindo na equação anterior, rearranjando termos e, de novo, invocando o teorema de Gauss para converter a divergência, no último termo acima, num fluxo, vem:

\(\frac{d}{dt}\left[\frac{1}{2}\int_{D}dV\left[(\frac{\partial \psi}{\partial t})^2+c^2(\nabla\psi)^2\right] \right]=\int_{D}dVc^2\sigma\frac{\partial \psi}{\partial t} +\int_{Σ}dS\overrightarrow{n}\cdot(c^2\frac{\partial \psi}{\partial t}\nabla\psi)\)

O 1° membro pode ser interpretado como a taxa de crescimento da energia total do campo contida no domínio D:

\(E=\frac{1}{2}\int_{D}dV\left[(\frac{\partial \psi}{\partial t})^2+c^2(∇\psi)^2\right]\)                   (13)

Reconhecemos aqui não só a “energia cinética” como uma “energia potencial”, ambas quadráticas na amplitude do campo, em total analogia com a energia de um oscilador harmónico.

No 2° membro da equação anterior, o 1° termo é a “potência da fonte exterior ao campo; o 2° termo é, então, interpretado como o fluxo de energia que entra no domínio através da sua superfície:

\(\overrightarrow{n}\cdot(c^2\frac{\partial \psi}{\partial t}∇\psi)= \) fluxo de energia (no entido \(-\overrightarrow{n}\) ) por unidade de área da superfície

Assim, o resultado acima obtido escreve-se, por palavras:

\(\frac{dE}{dt}=\) aumento, na unidade de tempo, da energia contida em D = potência realizada pela fontes contidas em D + fluxo de energia que entra através da superfície Σ que limita D.

É a lei genérica de conservação de energia.

Observação: As expressões atrás obtidas para a “quantidade de movimento” ou “energia cinética” do campo podem ser multiplicadas por constantes adequadas para as fazer coincidir com definições mais habituais. Será evidente que essas constantes irão afetar os segundos membros das equações deduzidas, não alterando, contudo, o significado das mesmas.

Exemplo: retomemos o problema da corda vibrante, mantendo a identificação \(\psi(x,t)\equiv \rho y(x,t)\) e \(c^2\sigma(x,t)\equiv f(x,t)\) (cf. eqs. 10 e 14). A energia cinética na porção do fio em 0 < x < b < a (é este o domínio D aqui unidimensional) é, naturalmente, \(K=\frac{1}{2}\int_{0}^{b} dx \rho(\frac{\partial y}{\partial t})^2\). Deste modo, a expressão genérica da energia (eq. 13) deverá ser dividida por ρ e, portanto, também se deve dividir por ρ o 2° membro da equação de conservação da energia. Lembrando que, para a corda vibrante é \(c^2=\frac{\tau}{\rho}\), obtemos, por simples adaptação das equações:

\(E=\frac{1}{2}\int_{0}^{b}dx\left[\rho(\frac{\partial y}{\partial t})^2+\tau(\frac{\partial y}{\partial x})^2\right]\)

obtém-se, assim:

\(\frac{dE}{dt} = \int_{0}^{b} dx f\frac{\partial y}{\partial t}+\tau(\frac{\partial y}{\partial t}\frac{\partial y}{\partial x})_{ x=b}\)

Neste caso, não há contribuição do outro extremo do intervalo considerado (x=0) devido à condição fronteira (extremo fixo, em qualquer instante).

Se, na expressão da densidade de força (f) explicitarmos a contribuição do peso, o 1° termo do 2° membro da equação anterior contem a contribuição:

\(-\int_{0}^{b} dx \, \rho g \frac{\partial y}{\partial t}=-\frac{d}{dt}\int_{0}^{b} dx \, \, \rho g\, \, y(x,t)\)

Assim, esta contribuição pode passar para o 1° membro da mesma equação, levando a redefinir a energia incluindo, agora, a energia potencial gravítica. Em qualquer caso, vemos que a taxa de crescimento da energia define o fluxo de energia \(\tau (\frac{\partial y}{\partial t}\frac{\partial y}{\partial x})_{x=b}\), a energia que entra, através do ponto B no intervalo 0 < x < b, por unidade de tempo.

Mas, voltando à expressão acima da energia, qual a origem do termo \(\frac{1}{2}\int_{0}^{b} dx \, \, \tau \, (\frac{\partial y}{\partial x})^2\), interpretado como energia potencial? Recordemos que a porção do fio em (x, x+ δx), na posição de referência, foi esticada, após a deformação, apresentando o comprimento atrás deduzido, nomeadamente, \(\delta\ell=\delta x\left[1+\frac{1}{2}(\frac{\partial y}{\partial x})^2\right]\). Nas extremidades desta porção atua a força tensora (τ) que, portanto, realiza o trabalho \(\tau (\delta\ell-\delta x)=\frac{\tau}{2}(\frac{\partial y}{\partial x})^2 \delta x\). Este trabalho, tal como numa mola, fica acumulado como energia potencial elástica.

O leitor poderá questionar as designações de “quantidade de movimento” ou “energia” do campo acima empregues. É verdade que essas designações ganham o sentido habitual no caso da corda vibrante. Mas será assim, em geral? A objeção tem todo o sentido porque aqueles conceitos são pertinentes à matéria e não se vê como eles se podem generalizar ao campo abstrato aqui tratado. Para responder à questão, teriamas que considerar o campo da matéria e fazer intervir uma interação entre os dois campos. Ver-se-ia, então, que a conservação genérica da quantidade de movimento ou da energia só se verifica se incluirmos, nas definições destas grandezas, quer a contribuição habitual do campo da matéria quer a contribuição do campo aqui considerado. Não iremos aqui considerar esta interessante conclusão.

Notas:

¹Ver o artigo “Escalares, vetores e tensores”.

²Também conhecido por teorema da divergência.