Graus de liberdade de um sistema molecular

Considerando uma associação de N átomos (molécula, ião, ou radical) em fase gasosa – isto é, isolada e livre de restrições externas ao seu movimento – cada um dos seus átomos pode deslocar-se segundo as três direções do espaço, descritas pelos eixos coordenados ou vetores x,y,z. Teremos assim 3N vetores que podem combinar-se em 3N movimentos distintos.

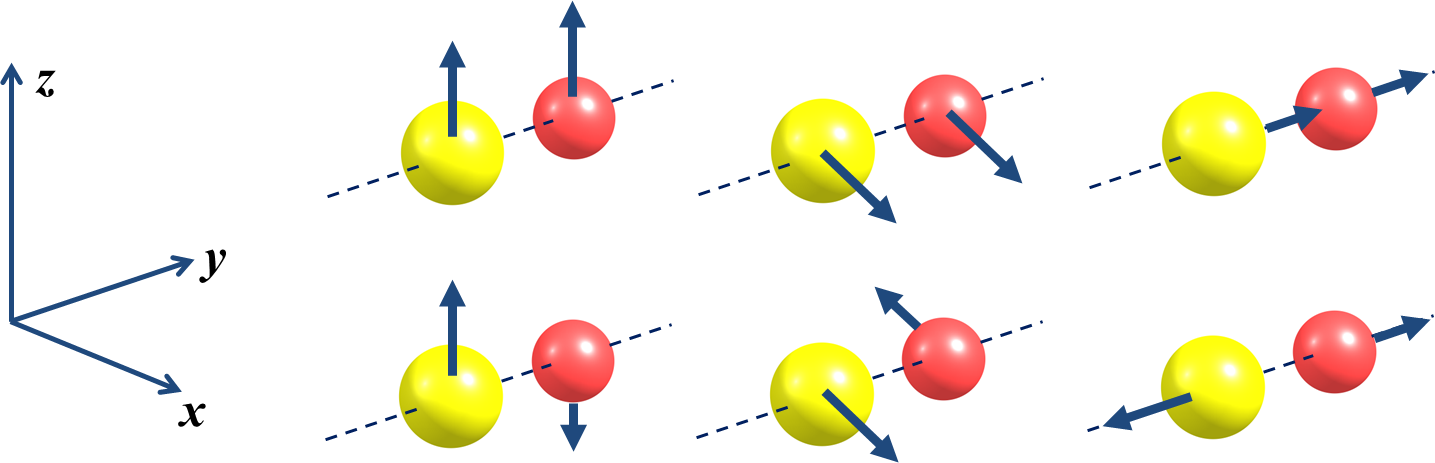
Quando todos os átomos se movem coordenadamente na direção um dado vetor (por exemplo, direção z: FIGURA 1, primeira imagem) isso representa a translação da molécula nessa direção. Para uma molécula isolada há pois três movimentos – ou graus de liberdade – translacionais.

De igual modo, é possível encontrar combinações de movimentos individuais dos átomos que resultam numa rotação da molécula em torno do seu centro de massa. Estes graus de liberdade rotacionais são também três para a maioria das moléculas. Em moléculas lineares, há apenas dois graus de liberdade rotacionais, pois não existe rotação em torno do eixo molecular (não moveria nenhum átomo).

As restantes combinações de movimentos atómicos resultam em movimentos dos átomos entre si, sem que haja translação ou rotação da molécula, ou seja, correspondem a graus de liberdade vibracionais. Deste modo, um sistema molecular com N átomos tem 3N-6 vibrações (3N-5 se for linear).

A solução da equação de Schödinger para uma partícula livre em movimento tem como significado físico a não-quantização da energia translacional. Dito de outro modo, os graus de liberdade translacionais são contínuos. Contudo, o mesmo não se passa com os movimentos os rotacionais e vibracionais, a que correspondem níveis de energia discretos (ou quantizados). Assim, é possível observar transições entre os níveis rotacionais (espectroscopia rotacional) ou entre os níveis vibracionais (espectroscopia vibracional). Como será discutido abaixo, numa molécula em fase gasosa é possível observar transições em que se alteram simultaneamente o estado vibracional e o estado rotacional (por vezes abreviadas para “transições roto-vibracionais”).

O modelo mais simples para descrever as vibrações moleculares é o modelo do oscilador harmónico diatómico: dois átomos de massa m₁ e m₂, ligados por uma mola perfeitamente elástica (FIGURA 2A). Os dois átomos oscilam em torno da distância de equilíbrio, num movimento que pode ser designado por “elongação linear” (e frequentemente abreviado para “elongação”).

Por resolução da equação de Schrödinger para este modelo, obtém-se a expressão da energia dos níveis vibracionais

\(E_v=h\nu(v+ ½)\)                    (1)

onde v é o número quântico vibracional (v = 0, 1, 2, 3, …) e ν é a frequência de vibração do oscilador harmónico. Segundo este modelo, os níveis de energia de um oscilador estão igualmente espaçados, sendo a diferença entre eles igual a hν (FIGURA 2B). A regra de seleção para o oscilador harmónico é Δv = 1, pelo que o espectro vibracional de uma molécula diatómica nesta aproximação consiste num único sinal de frequência ν, independentemente do nível de partida.

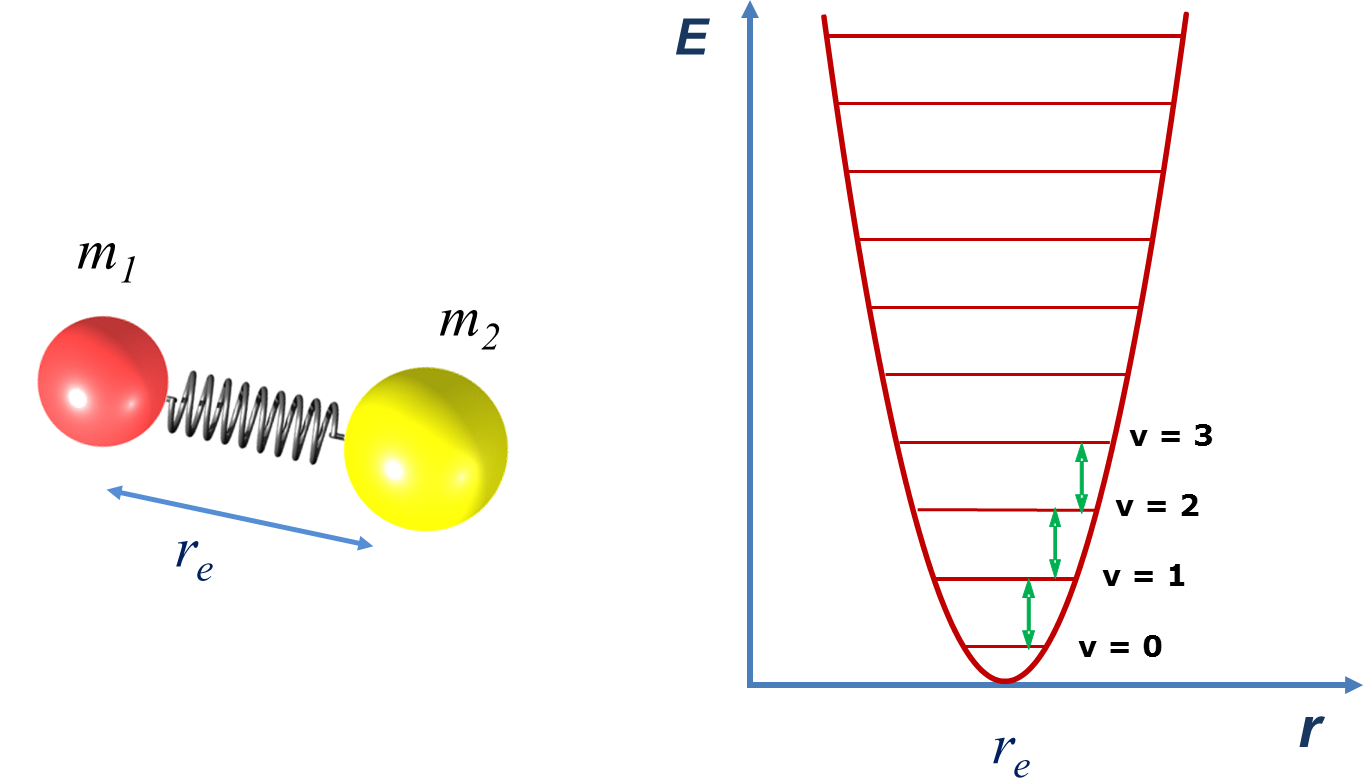
A frequência do oscilador depende naturalmente da força da “mola”, ou seja, do grau de rigidez/elasticidade da ligação química, que se traduz na constante de força da ligação, k. Esta constante de força é a que define a resistência da mola à deformação, ou seja, a força que é necessário efetuar para provocar uma deformação de Δx, de acordo com a lei de Hooke, F = k Δx. A equação da frequência do oscilador harmónico é então dada por

\(\nu=\frac{1}{2\pi}\sqrt{\frac{k}{\mu}}\)                    (2)

onde μ é a massa reduzida do oscilador.

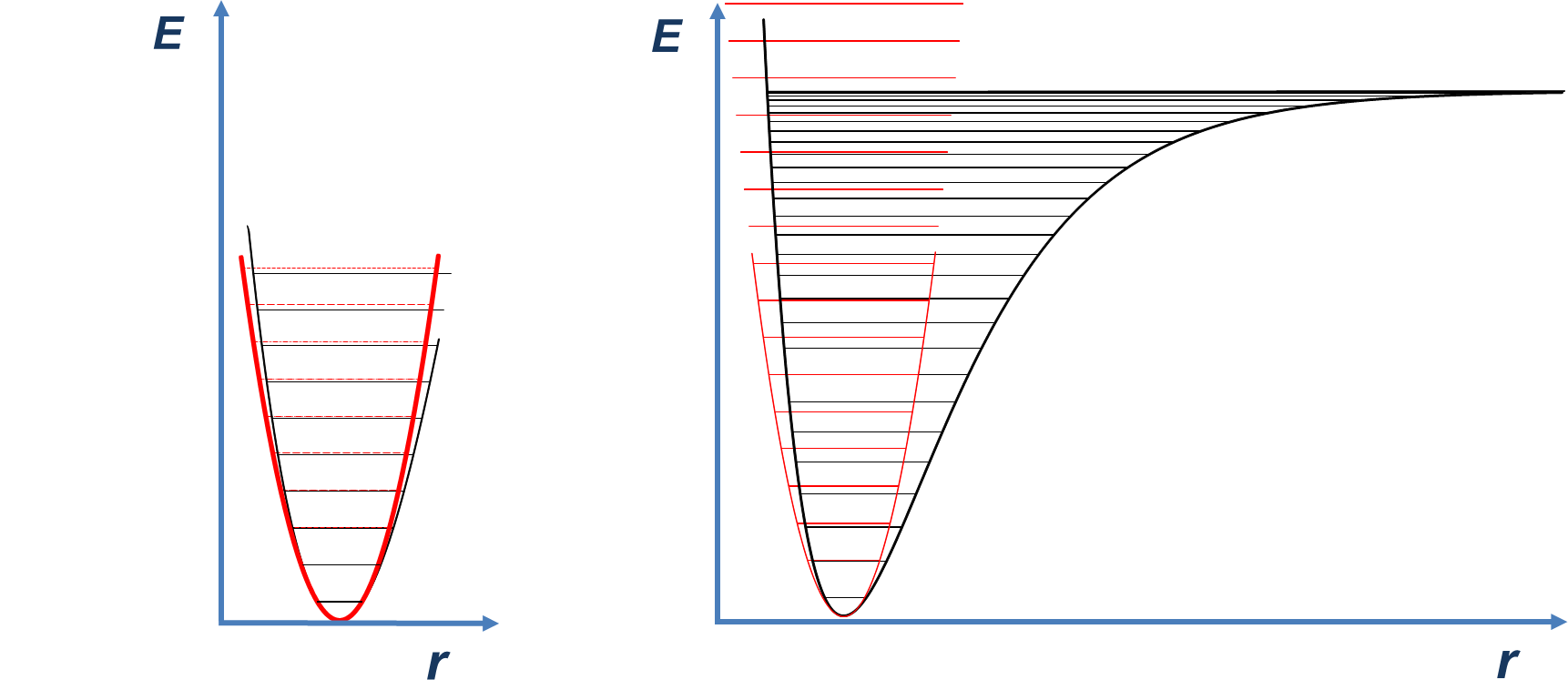
Os osciladores reais são anarmónicos, uma vez que as ligações químicas não se comportam como molas perfeitamente elásticas. A FIGURA 5 compara a função de energia potencial do oscilador harmónico com uma curva pouco anarmónica (FIGURA 3A) e muito anarmónica (FIGURA 3B). A situação real corresponde à curva de alta anarmonicidade (FIGURA 3B), já que as ligações químicas quebram quando são estiradas excessivamente.

A energia dos níveis de um oscilador anarmónico é dada por

\(E_v=h\nu(v+½)-h\nu x_e(v+½)^2\)                    (3)

onde \(x_e\) é a constante de anarmonicidade, específica de cada oscilador.

Um efeito imediato da anarmonicidade é a diminuição progressiva do espaçamento energético entre os níveis (tal como se observa na FIGURA 3).

\(ΔE_{v_{0→1}}=h\nu(1-2x);\)             \(ΔE_{v_{1→2}}=h\nu(1-4x);\)             \(ΔE_{v_{2→3}}=h\nu(1-6x);\)                           (4)

Próximo da energia de dissociação, o espaçamento tende para zero, o que permite estimar a energia de uma ligação a partir da sua frequência de vibração e da correspondente anarmonicidade:

\(D_e=h\nu/4x_e\)                    (5)

A regra de seleção para o oscilador anarmónico é Δv = 1, 2, 3, … sendo possível observar diversas transições. Enquanto a transição do nível v=0 para v=1 é designada por transição fundamental, as transições de v=0 para v>1 são designadas sobretons.

Quando a população dos níveis excitados é significativa, é possível observar as transições v=1 para v=2, v=2 para v=3, etc. Estas transições aumentam de intensidade por aumento da temperatura (ver distribuição de população de Boltzmann) pelo que as correspondentes bandas do espectro vibracional são designadas por “bandas quentes”.

Esta análise do espectro vibracional de sistemas diatómicos pode estender-se a sistemas poliatómicos. Em sistemas poliatómicos, observam-se vários movimentos de “elongação linear” (tantos quantos as ligações entre 2 átomos), de “deformação angular” (envolvendo 3 átomos ligados), de “torção” e de “deformação para fora do plano” (envolvendo 4 átomos ligados). Estes movimentos combinam-se nas 3N-6 vibrações globais da molécula, designados por modos normais de vibração. Em alguns casos, os modos normais de vibração estão altamente localizados num grupo definido de átomos – por exemplo, o grupo carbonilo (C=O) – e originam bandas no espectro vibracional que são caraterísticas desse grupo de átomos e mais ou menos independentes do resto da molécula. Estas vibrações são designadas por frequências de grupo, muito utilizadas em caraterização química. Estes tópicos serão desenvolvidos num texto próprio.

Transições roto-vibracionais numa abordagem breve

Tal como referido acima, é possível observar transições vibracionais (Δv = 1, 2, 3 …) acompanhadas de transições rotacionais (ΔJ= 1). Considerando estes graus de liberdade como independentes entre si, a energia dos níveis num oscilador diatómico é dada simplesmente pela soma da equação (3) com a equação do rotor diatómico:

\(E_{v,J}h\nu(v+½)+BJ(J+1)-[h\nu x{_e}(v+½)^2+DJ^2(J+1)^2] \)                     (6)

Ignorando os termos anarmónico e de distorção centrífuga – indicados entre parêntese rectos –, a energia da transição vibracional fundamental num oscilador diatómico é dada por

\(ΔE_{v=0→v=1} = h\nu + B[J(J+1)−J’(J’+1)]\)

onde J é o número quântico rotacional do estado inicial, v=1, e J’ é o número quântico rotacional do estado final, v = 1.

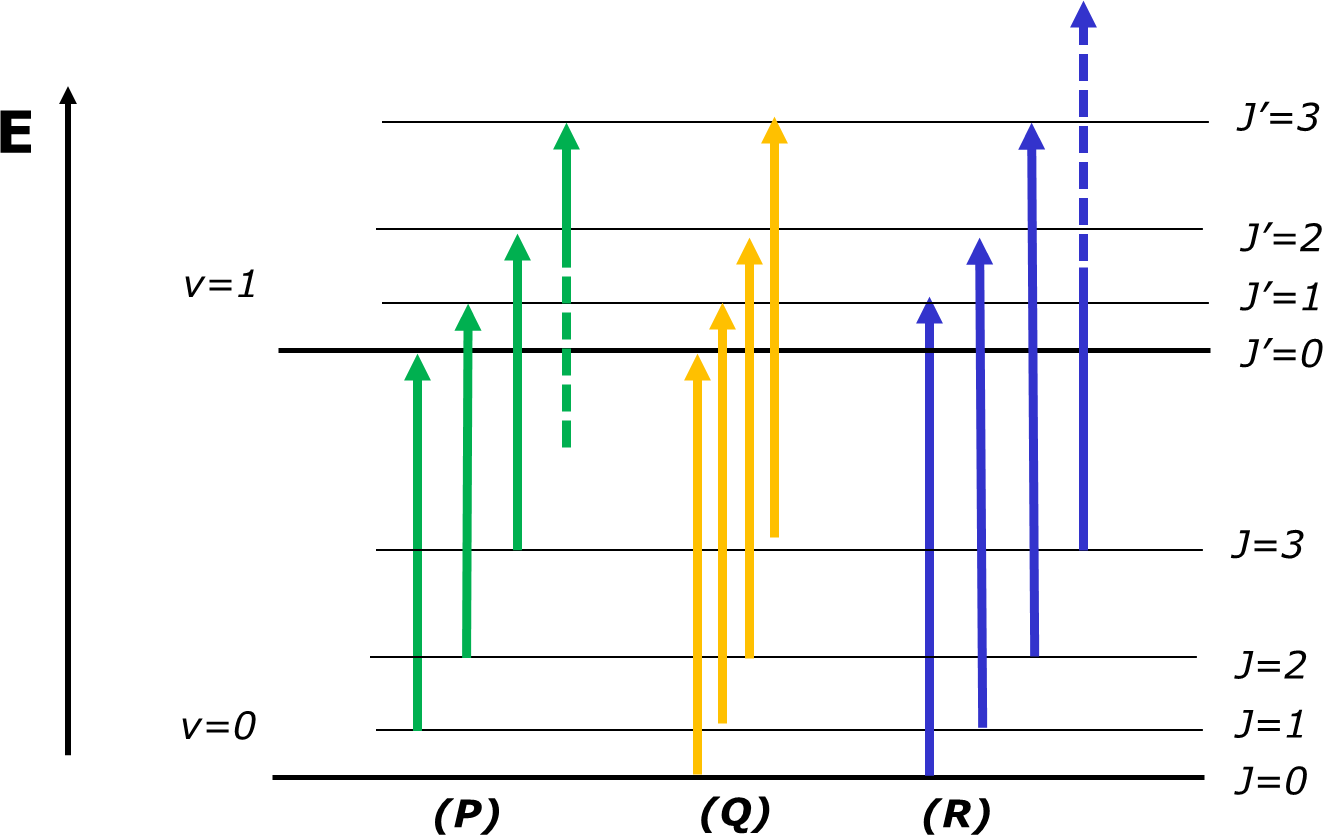
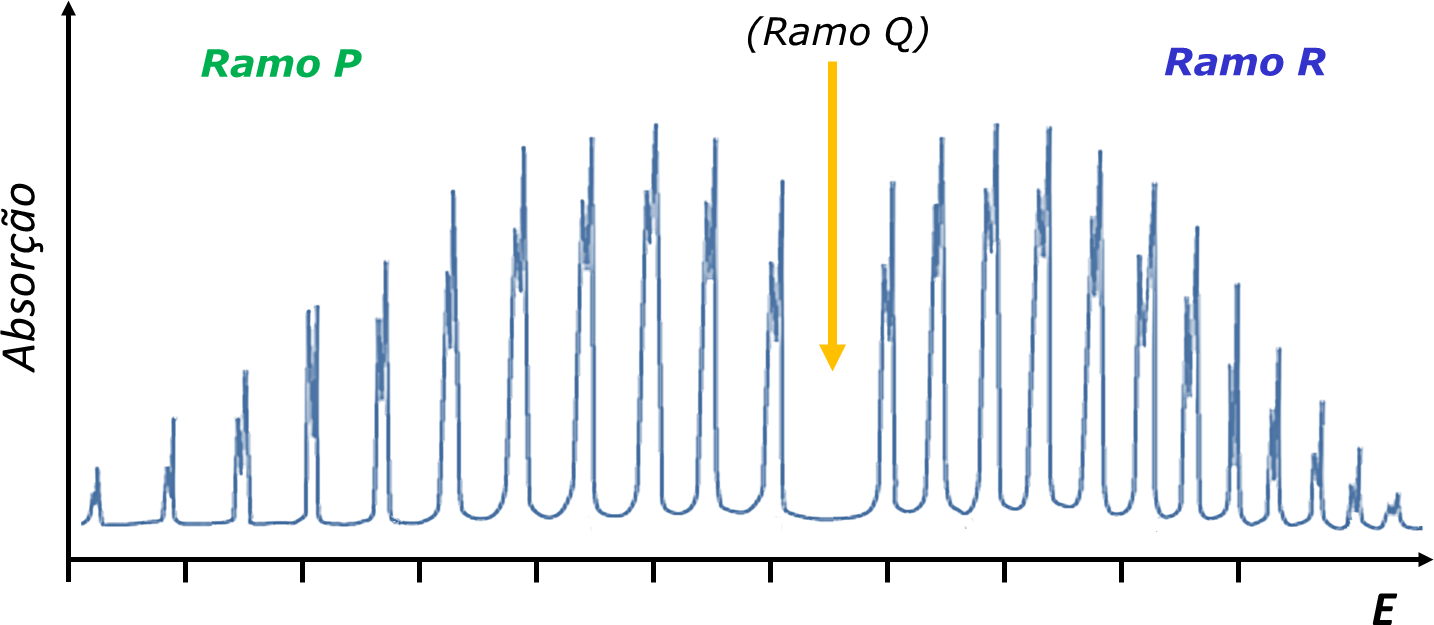
A FIGURA 4 ilustra as transições que correspondem a J’=J-1, J’=J e J’=J+1 e a FIGURA 5 apresenta o espectro observado para o oscilador diatómico real HCl. No espectro real, o efeito da anarmonicidade do oscilador no valor de B é evidente.