O pêndulo também pode ser posto a rodar em torno da vertical, um movimento que tantas vezes observamos quando, distraidamente, fazemos girar as chaves de casa ou do automóvel suspensas por uma fina corrente. Estes dois tipos de movimento - oscilação e rotação - correspondem aos dois graus de liberdade que o pêndulo apresenta, por exemplo, o ângulo θ que o fio faz com a vertical e o ângulo ϕ que o plano do pêndulo, definido pelo fio e pela vertical passando pelo ponto de sustentação, faz com um outro plano vertical fixo. Estes dois movimentos só em situações simples se apresentam separados - no caso geral, eles interferem mutuamente originando uma riqueza de comportamentos que nos surpreende.

Se a Terra não rodasse, um pêndulo manteria invariante (i.e., imóvel) o seu plano de oscilação. Mas a Terra roda, o que torna o movimento do pêndulo ainda mais interessante porque somos obrigados a considerar a força de Coriolis originada por a Terra não ser um referencial inercial. Uma imediata consequência deste facto é a rotação do plano do pêndulo. Este pêndulo de Foucault, como passou a ser conhecido, permite-nos determinar a latitude do lugar onde o pêndulo se situa.

É interessante observar que o movimento do pêndulo é inteiramente equivalente ao movimento de uma pequena esfera rígida na superfície interior de uma esfera oca, de raio igual ao comprimento do fio.

Neste artigo, é apresentada a análise genérica, mas detalhada, do movimento do pêndulo simples, ignorando, primeiro, a rotação da Terra, para, depois, se estudar o pêndulo de Foucault.

Descrição mecânica

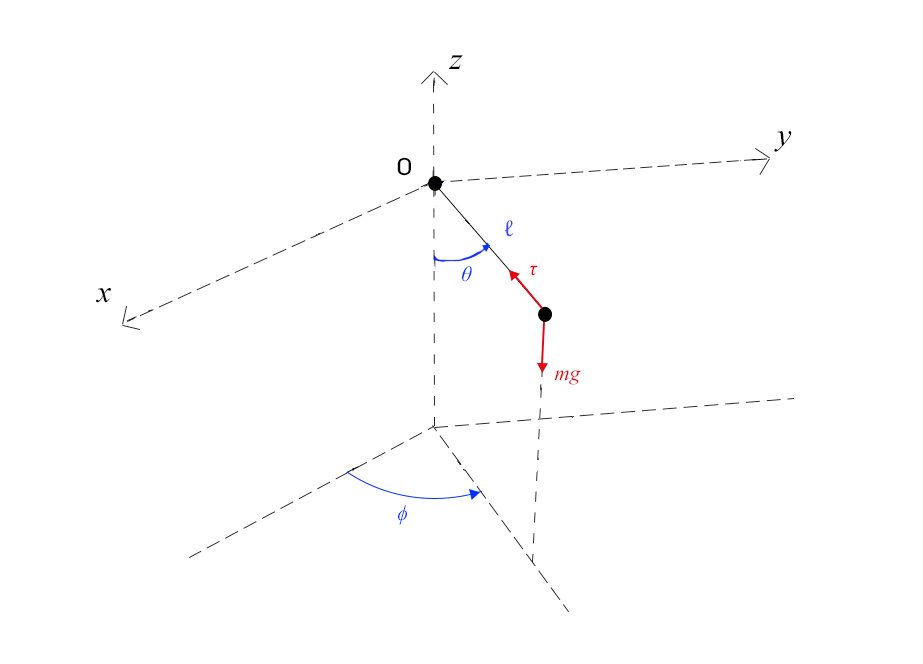
A FIGURA 2 mostra a caracterização dos dois graus de liberdade do pêndulo e as forças que sobre ele atuam. Consideramos um sistema tri-rectangular de eixos \(Oxyz\) com origem no ponto de suspensão, eixo \(z\) vertical. Este eixo e o fio, de comprimento ℓ, definem o plano do pêndulo e permitem a sua caracterização mecânica através dos ângulos \(\theta\) que o fio faz com a vertical e \(\phi\) que o plano do pêndulo faz com um outro plano vertical fixo, contendo a origem (na figura, o plano \(x\),\(z\)). Indicamos, também, as forças que se fazem sentir sobre a massa \(m\) presa na extremidade livre do fio: o seu peso, \(mg\), vertical e a tensão \(τ\) exercida pelo fio. Daqui resulta uma imediata e importante consequência: o fio pode puxar a massa, mas não a pode empurrar, pelo que:

\(τ ≥ 0\)            (1)

Se esta condição não se verificar, o fio deixa de estar esticado e o movimento tem que passar a incluir a distância à origem como uma nova variável dinâmica, i.e., o sistema terá três graus de liberdade.

Posto isto, a lei fundamental da dinâmica escreve-se:

\(m\vec{a}=m\vec{g}+\vec{τ}\)            (2)

Note-se que a energia mecânica conserva-se: o peso deriva de um potencial e a tensão não realiza trabalho, com o fio esticado, e desaparece se ele deixar de estar esticado. Há três incógnitas no problema: os dois ângulos \(\theta\) e \(\phi\) e a tensão τ. É conveniente usarmos uma base local definida por três versares ortonormados (FIGURA 3):

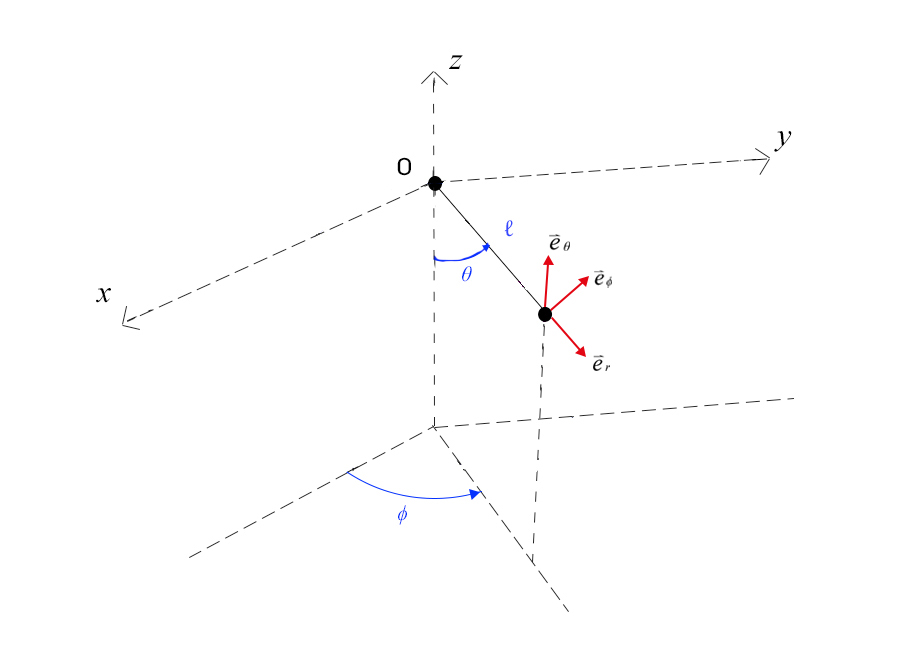
\(\vec{e}_{r}\): aponta da origem para a massa

\(\vec{e}_{\phi}\): perpendicular ao plano do pêndulo, com o sentido em que \(\phi\) cresce

\(\vec{e}_{\theta}\): no plano do pêndulo, perpendicular ao eixo, com o sentido em que \(\theta\) cresce

O conjunto (\(\vec{e}_{r}\), \(\vec{e}_{\phi}\), \(\vec{e}_{\theta}\)), nesta ordem, forma um referencial

direto:

\(\vec{e}_{r}\times \vec{e}_{\phi}=\vec{e}_{\theta}\)            (3)

Da figura, obtém-se facilmente as componentes cartesianas destes versares:

\(\vec{e}_{r} = (sen \ \theta \ cos\ \phi, sen \ \theta \ sen \ \phi, - cos\ \theta)\)

\(\vec{e}_{\theta} = (cos \ \theta \ cos\ \phi, cos\ \theta \ sen\ \phi, sen\ \theta) =\frac{\partial \vec{e}_r}{\partial \theta}\)

\(\vec{e}_{\phi} = (-sen\ \phi, cos\ \phi, 0)\)

Posto isto, partindo do vector de posição da massa:

\(\vec{r}=ℓ\vec{e}_{r}\)            (4)

obtemos a expressão da velocidade derivando em ordem ao tempo:

\(\vec{v}=\ell\frac{d \vec{e}_r}{dt}=\ell\left[\frac{\partial \vec{e}_r}{\partial\theta }\theta^.+\frac{\partial \vec{e}_r}{\partial\phi }\phi^.\right]=\ell\left[\theta^.\vec{e}_\theta+\phi^.\ sen\ \theta \ \vec{e}_\phi\right]\)            (5)

e, com um pouco mais de trabalho, a sua aceleração:

\(\vec{a}=\ell\left[-(\dot{\theta}^{2}+\dot{\phi}^{2}sen^2\theta) \vec{e}_r+(\ddot{\theta}-\dot{\phi}^{2}sen \ \theta \ cos \ \theta) \ \vec{e}_\theta + (2 \ \dot{\phi}\dot{\theta} \ cos \ \theta \ + \ \ddot{\phi} \ sen \ \theta)\vec{e}_\phi\right]\)            (6)

Notando que \(\vec{\tau}=-\tau\vec{e}_r\) e \(\vec{g}=-g \ \vec{e}_z=-g \ (sen \ \theta \ \vec{e}_\theta- cos \ \theta \ \vec{e}_r)\), podemos reescrever as eqs. (2) sob a forma das três seguintes equações para as suas componentes na base local:

\(-m\ \ell \left[\dot{\theta}^2+\dot{\phi}^2 \ sen^2 \theta\right]=-\tau + mg\ cos\ \theta\)             (7a)

\(m\ \ell \left[\ddot{\theta}+\dot{\phi}^2 \ sen\ \theta \ cos\ \theta\right]=-mg \ sen \ \theta\)            (7b)

\(m\ \ell \left[2\ \dot{\phi} \dot{\theta} \ cos\ \theta \ + \ddot{\phi} \ sen \ \theta \right]=0\)            (7c)

Esta última equação reescreve-se como:

\(\frac{1}{sen\ \theta}\frac{d}{dt}(\dot{\phi} \ sen^2 \ \theta)=0\)

Encontramos, assim, um integral primeiro:

\(\dot{\phi }sen^{2}\theta \)= constante            (8)

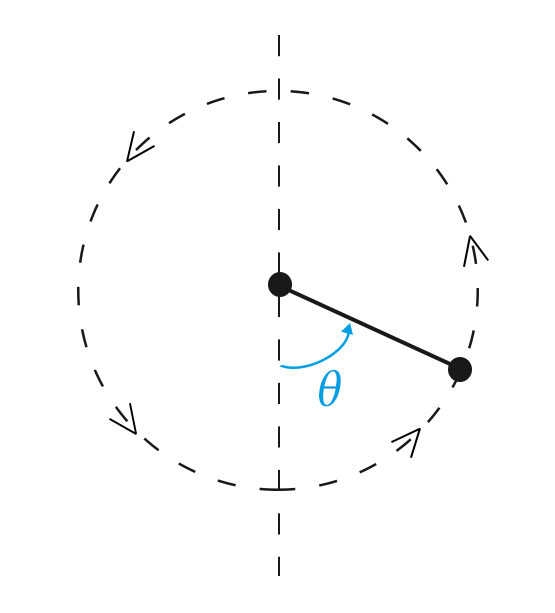
Qual a origem física deste resultado? Observando a FIGURA 1, vemos que, se se considerar o momento das forças com pólo na origem, apenas o peso contribui, sendo, pois nula, a sua projeção vertical. Então, pelo teorema dos momentos cinéticas, deverá ser constante a componente \(L_z\) . Ora:

\(\vec{L}=\vec{r} \ \times \ (m \ \vec{v})= m \ell^2\left[- \dot{\theta} \ \vec{e}_\phi \ + \dot{\phi} \ sen \ \theta \ \vec{e}_\theta\right]\)            (9)

Assim, introduzindo as componentes cartesianas dos versores \(\overrightarrow{e}_\theta\) e \(\overrightarrow{e}_\phi\), obtemos:

\(L_z= m\ \ell^2 \ \dot{\phi} \ sen^2 \ \theta=\) constante

o que justifica a eq. (8).

Este sistema também conserva a energia mecânica: a tensão do fio não realiza trabalho e o peso deriva de uma energia potencial. Ora, a energia mecânica é:

\(E=\frac{1}{2}m\vec{v}^2 \ + \ mgz = \frac{1}{2}m \ \ell^2 \ (\dot{\theta}^{2} \ + \ \dot{\phi}^{2} \ sen^2 \ \theta)- mg\ell \ cos \ \theta\)             (10)

\(\frac{dE}{dt}=0\rightarrow m \ \ell^2 \ \dot{\theta} \ (\ddot{\theta}\ + \dot{\phi}^2 \ sen\ \theta \ cos \ \theta) \ + \ m \ \ell^2 \ \dot{\phi} \ \ddot{\phi} \ sen^2 \ \theta + mg\ell \ \dot{\theta} \ sen \ \theta = 0\)

Eliminando \(\ddot{\phi}\) pela eq. (7c), e simplificando o resultado, obtemos a eq. (7b).

Estes dois resultados mostram que as equações do movimento (7b) e (7c) são equivalentes, respetivamente, às conservações da energia mecânica e da componente vertical do momento cinético. Poderiamos, até, partir destas leis de conservação para deduzir rapidamente as equações do movimento. Não obteríamos, contudo, a eq. (7a) que fornece a tensão do fio, submetida à desigualdade expressa na eq. (1). É precisamente daqui que decorre uma grande riqueza de comportamentos do pêndulo como, a seguir, se analisa com alguns casos particulares.

a) Solução \(\theta ≡ \theta_0 =\) constante \(≠ 0\) (\(\theta_0 = 0\) não corresponde a qualquer movimento!)

A eq. (7c) dá:

\(\ddot{\phi}\ sen\ \theta_0=0 \ \rightarrow \ \ddot{\phi}=0\)

O pêndulo executa uma rotação circular em torno da vertical. Mas nem todas as configurações para tais rotações são possíveis; de facto, a eq. (7a) mostra que:

\(\frac{\tau}{m}=g\ cos\ \theta_0 \ + \ell \dot{\phi}^{2}\ sen^2\ \theta_0=g\ (cos\ \theta_0 + \frac{sen^2\ \theta_0}{cos \ \theta_0})= \frac{g}{cos\ \theta_0}\)

onde se usou a eq. (7b) para eliminar \(\dot{\phi}^2\). Assim, a condição (1) exige:

\(\tau \geq 0 \rightarrow \theta_0 \leq \frac{\pi}{2}\)

A FIGURA 4 exibe este movimento para o qual \(\dot{\phi}^2=\frac{g}{l \ cos \ \theta_0}\).

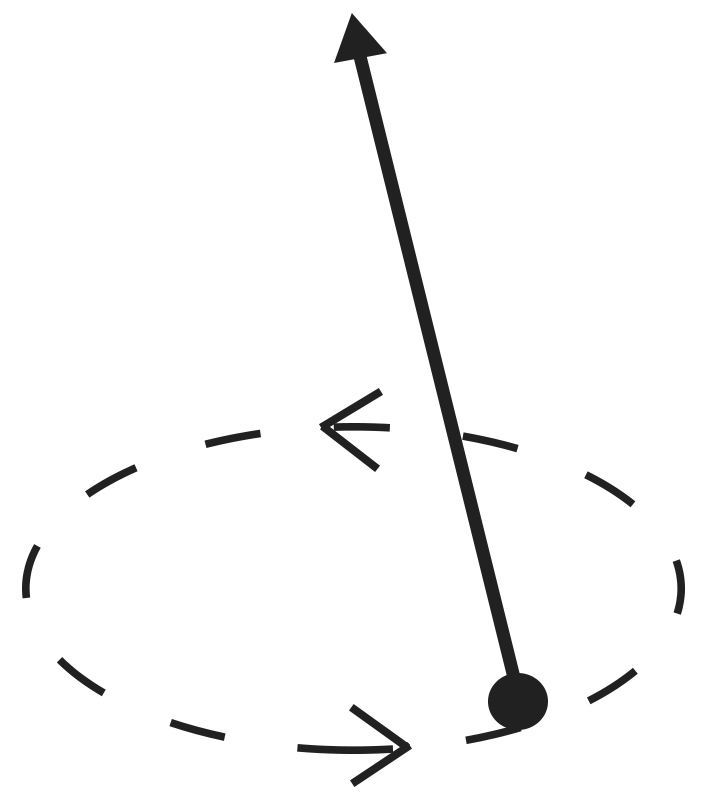
Que aconteceria se tentássemos fazer rodar o pêndulo acima do plano horizontal passando pelo ponto de suspensão, i.e., \(\theta_0 > \frac{\pi}{2}\) ? A eq. (1) seria violada: o fio não permaneceria esticado e a massa “cairia” para o interior da esfera imaginária, de centro naquele ponto e raio \(l\), o que nos obrigaria a discutir o movimento subsequente com mais um grau de liberdade (a distância à origem).

b) Solução \(\phi \ \equiv \ \phi_0 =\) constante \(\rightarrow L_z = 0\)

Agora, o plano do pêndulo é invariante, mas diversos comportamentos dinâmicos são possíveis, dependendo das condições iniciais. Reescrevamos as equações básicas sob a forma:

\(\frac{\tau}{ml}=\omega_0^2 \ cos \ \theta \ + \dot{\theta}^2 \geq 0\)

\(\ddot{\theta}+\omega_0^2 \ sen \ \theta =0 \rightarrow E =m\ell^2(\frac{\dot{\theta}^2}{2}-\omega_0^2 \ cos \ \theta)\)

onde:

\(\omega_0^2 \equiv \frac{g}{l}\)            (11)

   (i) Para oscilações de pequena amplitude (\(\theta << 1\)), é sempre \(\tau > 0\) e a equação de movimento reduz-se à equação de um oscilador harmónico de frequência natural \(\omega_0\):

\(\ddot{\theta}+\omega_0^2 \ \theta=0\)            (12)

Trata-se de um movimento oscilatório com aquela frequência.

   (ii) Consideremos, agora as seguintes condições iniciais:

\(\dot{\theta}(0)=0 \ \ \ \ \ \ \ \ \ \ \theta(0)=\theta_0\neq0\)

O pêndulo é largado com velocidade nula na posição \(\theta_0\), mas esta não pode ser qualquer porque o valor inicial da tensão, \(\tau(0)=ml \ \omega_0^2 \ cos \ \theta_0\), exige \(\theta_0\leq\frac{\pi}{2}\) o pêndulo não pode ser largado acima do plano horizontal passando pela origem. Uma vez assegurada esta condição, a conservação da energia mecânica dá, imediatamente, a velocidade:

\(\frac{\dot{\theta}^2}{2}=2\ \omega_0^2(cos\ \theta \ - \ cos \ \theta_0 )\)

Assim, a oscilação dá-se no intervalo \(-\theta_0 ≤ \theta ≤ \theta_0\), como se representa na FIGURA 5.

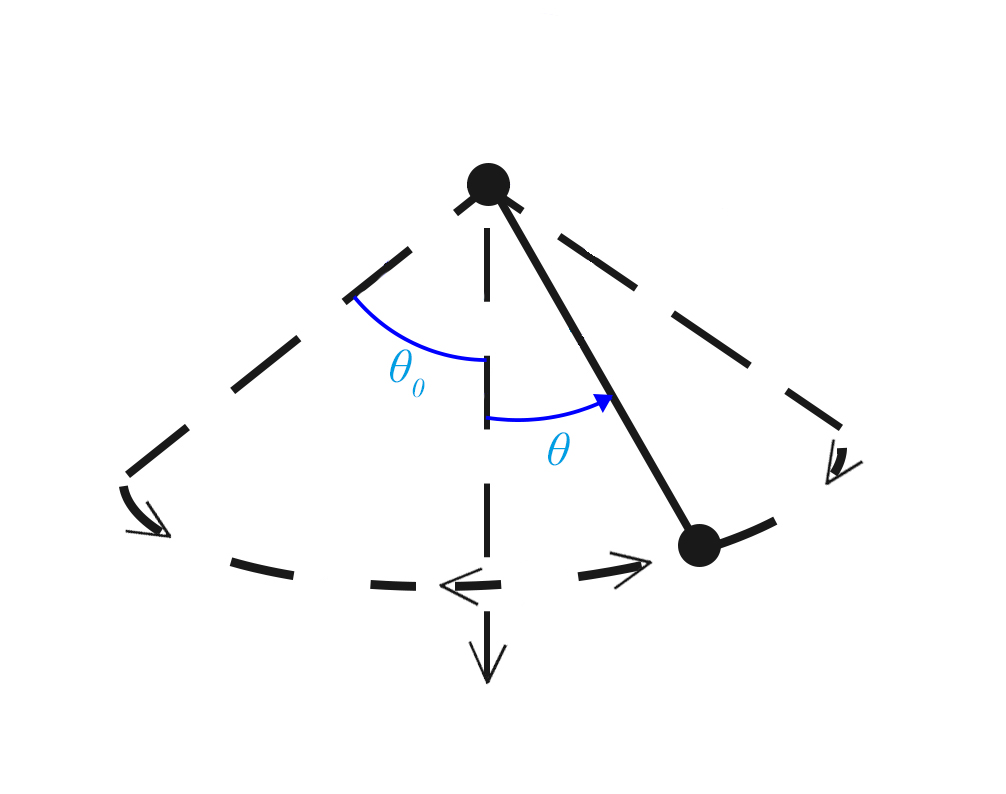
   (ii) Analisemos, agora, o que se passa com as condições iniciais:

\(\dot{\theta}^(0)=\dot{\theta}_0 \neq0 \ \ \ \ \ \ \ \ \ \ \theta(0)=0\)

Tal corresponde a dar um impulso ao pêndulo quando este se encontra na posição de equilíbrio. Da conservação da energia mecânica resulta:

\(\dot{\theta}^2=\dot{\theta}_0^2 - 2\ \omega_0^2 \ (1-cos\ \theta)\)            (13a)

Há várias hipóteses a considerar devido à condição sobre a tensão do fio:

\(\frac{\tau}{ml}=\dot{\theta}^2-\omega_0^2 \ (2-3cos \ \theta)\)            (13b)

1ª Se \(\dot{\theta}_0^2 \geq 5 \ \omega_0^2\) o pêndulo gira no plano vertical, efetuando um movimento circular (FIGURA 6). Com efeito, mesmo para \(\theta = \pi\), é \(\tau ≥ 0\) , tendo o pêndulo velocidade no seu ponto mais alto: \(\dot{\theta}^2=\dot{\theta}_0^2-4 \ \omega_0^2\) para \(\theta = \pi\). Trata-se, pois, de um rotação do pêndulo.

2ª Se \(2 \ \omega_0^2\ < \ \dot{\theta}_0^2\ < \ 5 \ \omega_0^2\), o movimento pendular não é possível porque a tensão anula-se numa posição \(\theta^*\) na qual o pêndulo ainda se move.

Com efeito, \(\theta^*\), para o qual é \(\tau = 0\), é determinado por \(cos\ \theta^* =\frac{1}{3}(2-\frac{\dot{\theta}_0^2}{\omega_2^0})\), vindo \(\theta^*\) real para \(\dot{\theta}_0^2\) no intervalo considerado. Mas, nesse ponto, é: \(\dot{\theta}^2 =\frac{1}{3}(\dot{\theta}_0^2-2 \ \ \omega_0^2)>0\). O anulamento da tensão, com o pêndulo ainda em movimento, significa que o fio deixa de estar esticado e a massa “cai” para o interior da esfera de raio l, passando a ter de ser descrito com os três graus de liberdade já referidos.

3ª Se \(0\leq \theta_0^.2\leq 2\ \omega_0^2\), o pêndulo executa um movimento oscilatório situado no intervalo \(-\theta_M \leq \theta \leq \theta_M\), onde \(\theta_M\) é o ponto onde se anula a velocidade, i.e.,

\(cos\ \theta_M = 1-\frac{\dot{\theta}_0^2}{2\omega_0^2}\geq0 \ \ \rightarrow \ \ 0<\theta_M\leq \frac{\pi}{2}\)

Nesse ponto, a tensão é não negativa:

\(\frac{\tau}{ml}=\omega_0^2 \ cos \ \theta_M \geq 0\)

Este caso contem, evidentemente, as pequenas oscilações atrás tratadas.

O pêndulo de Foucault

Qual o efeito da rotação da Terra no movimento de um pêndulo? Para um observador terrestre, somos obrigados a considerar as forças inerciais, destas, a única que importa é a força de Coriolis:

\(\vec{F}_c=-2m \ \vec{\omega}_T \ \times \vec{v}\)            (14)

onde \(\vec{\omega}_T\) é o vector rotação instantânea da Terra (Com efeito, a rotação da Terra pode ser considerada uniforme e com eixo fixo em escalas de tempo da ordem de milhares de anos; os outros termos das forças inerciais, exceto Coriolis adicionam a força centrífuga à força da gravidade, originando a definição de \(\vec{g}\) e a sua dependência na latitude). Vemos já, embora qualitativamente, que o plano de oscilação de um pêndulo não é mais invariante: a força de Coriolis, perpendicular à velocidade, obriga este plano a rodar. Procedamos à análise quantitativa considerando o caso habitual de pequenas oscilações, o que nos irá garantir que o fio permanece tenso. Para isso, é conveniente considerar, agora, um referencial cartesiano com origem no ponto de suspenção do pêndulo e com os eixos assim definidos (FIGURA 7):

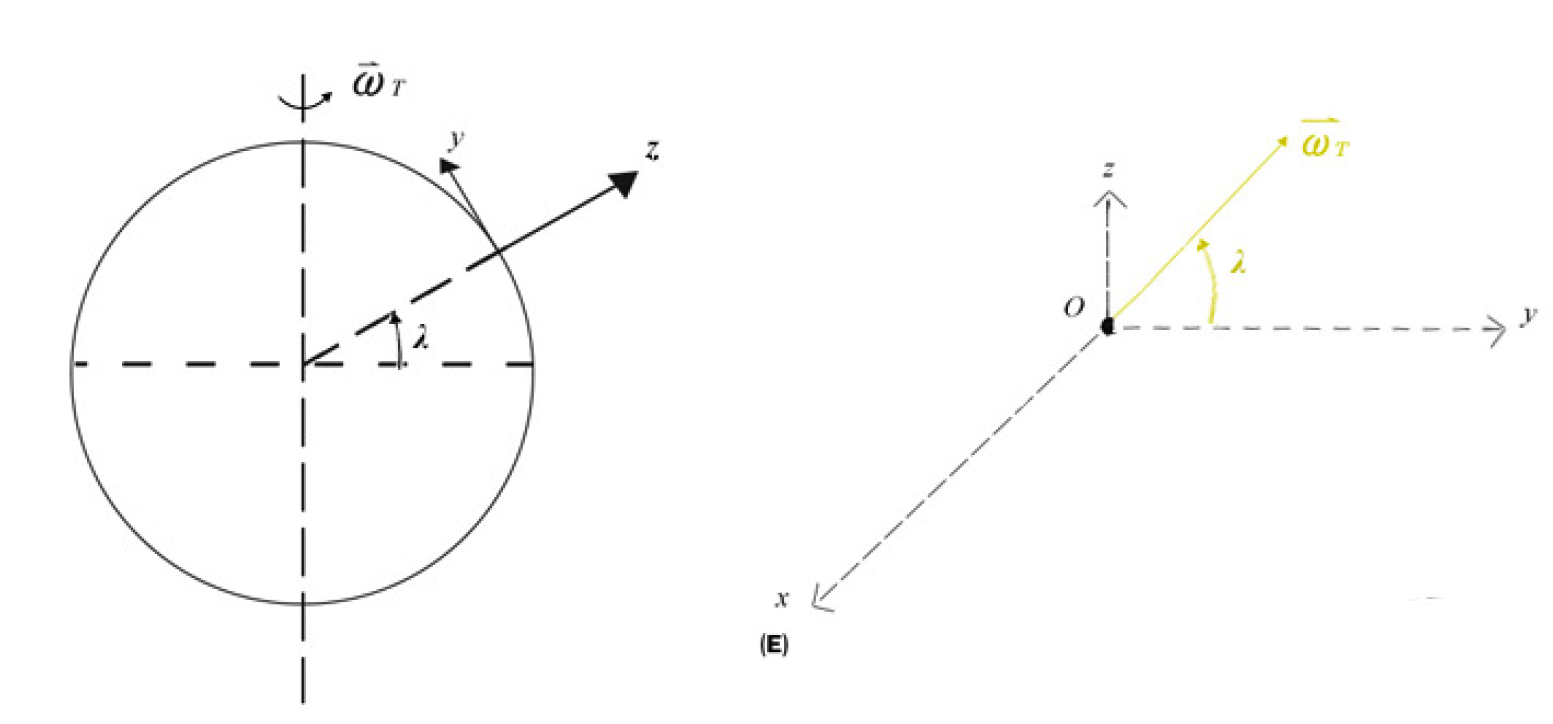
eixo \(z\): vertical do lugar (dirigido para cima)

eixo \(y\): tangente ao meridiano do lugar, apontando para Norte

eixo \(x\): tangente ao paralelo do lugar, apontando para Este.

Deste modo, o vector \(\vec{\omega}_T\) situa-se no plano (\(yz\)) fazendo um ângulo \(λ\) (latitude do lugar) com o eixo \(y\).

Para a análise do movimento, basta-nos estudar a evolução do momento cinético:

\(\frac{d\vec{L}}{dt}=\vec{M}=\vec{r}\ \times \ (m\vec{g}) - 2m\vec{r} \ \times \ (\vec{\omega_T} \ \times \ \vec{v})=\vec{r} \ \times (m\vec{g})+2m \ \vec{r} \cdot \vec{\omega}_T \ \vec{v}\)

onde se atendeu a que \(\vec{r}\cdot\vec{v}=0\) (fio permanece esticado). Usando a expressão do momento cinético atrás obtida, eq. 9, é imediato escrever as equações do movimento:

\(\ddot{\theta}-\dot{\phi}^2 \ sen \ \theta \ cos \ \theta = -\omega_0^2 \ sen \ \theta - 2 \ (\vec{e}_r\cdot\vec{\omega}_T) \ \dot{\phi} \ sen\ \theta\)            (15a)

\(2 \ \dot{\phi} \ \dot{\theta} \ cos \ \theta \ + \ \ddot{\phi} \ sen \ \theta =2 \ (\vec{e}_r\cdot\vec{\omega}_T) \ \dot{\theta}\)            (15b)

estas equações generalizam as eqs. (7b) e (7c) ao incluírem os efeitos da rotação da Terra.

Ora, \(\vec{\omega}_T\) tem as componentes cartesianas \(\vec{\omega}_T= \omega_T \ (0, cos \ \lambda, sen \ \lambda)\), pelo que:

\(\vec{e}_r \cdot \ \vec{\omega}_T= \omega_T \ (cos \ \lambda \ sen \ \theta\ cos \ \phi \ -sen \ \lambda \ cos \ \theta)\)

Para pequenas amplitudes de oscilação do pêndulo (\(\theta << 1\)), vem:

\(\vec{e}_r \cdot \ \vec{\omega}_T \cong - \ \omega_T \ sen \ \lambda\)

pelo que a eq. (15b) admite a solução:

\(\phi^.=- \ \omega_T \ sen \ \lambda\) = constante             (16)

(Para uma dedução mais simplificada deste resultado, ver “Pêndulo de Foucault”)
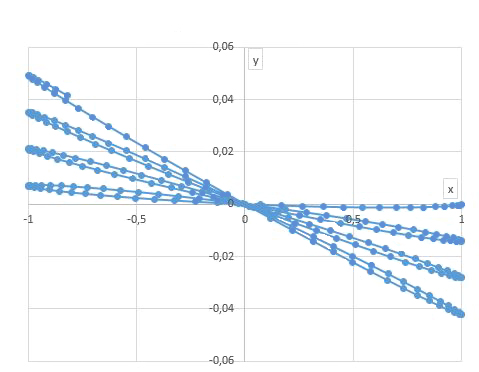
Quer dizer, o plano do pêndulo roda, em torno da vertical, no sentido dos ponteiros do relógio no hemisfério Norte (\(\lambda > 0\)) e no sentido contrário no hemisfério Sul (\(\lambda < 0\)). Esta rotação é uniforme e informa diretamente sobre a latitude do lugar, como se mostra na FIGURA 8.

Finalmente, a eq. (15a) mostra que o período de oscilação do pêndulo é alterado:

\(\omega_0 \ \ \ \ \ \ \rightarrow \ \ \ \ \ \ \sqrt{\dot{\phi}^2 +\omega_0^2}\)

Porém, esta alteração é, praticamente, impercetível para as condições experimentais habituais ( \(ω_0 >> ω_T\)).

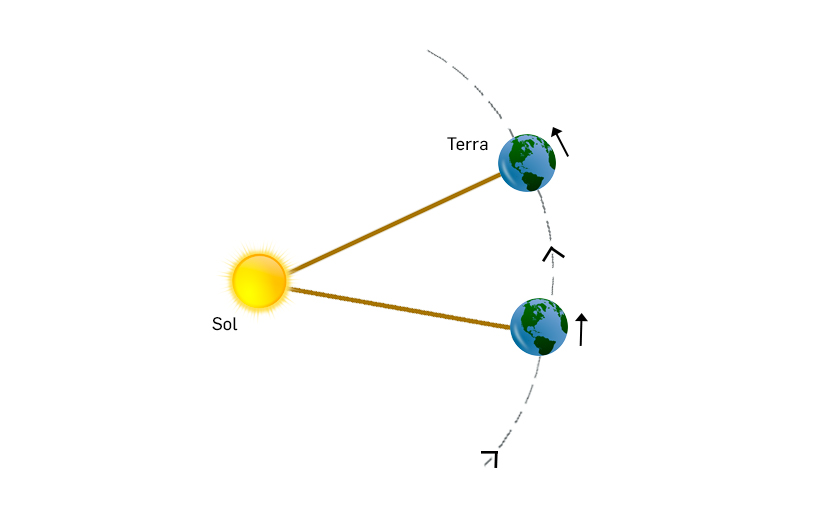
Tem interesse, neste contexto, analisar o valor de \(ω_T\). Como a Terra efetua uma rotação completa em 24h, poder-se-ia pensar que \(ω_T\approx\frac{2\pi}{24\times3600}s^{-1}\).Mas não é assim! Com efeito, um dia, i.e., 24 h é o tempo que decorre, para um observador na Terra, para o mesmo ponto do planeta se encontrar alinhado com o Sol. Mas, durante esse tempo, a Terra também se deslocou no seu movimento de translação em torno do Sol, que também é uma rotação. Para simplificar, aceitemos que este movimento é circular uniforme, realizando-se no mesmo sentido que a rotação da Terra (FIGURA 8). Então, ao fim de 24 h, a Terra rodou um pouco mais que \(2\pi\) e este excesso acumula-se exatamente em \(2\pi\) ao fim de um ano, quando a Terra regressa à sua posição inicial. Quer dizer, para um observador no Sol, considerado como observador inercial para quem \(\omega_T\) é definido, a Terra rodou 366 vezes no tempo correspondente a 365 dias terrestres, i.e., \(\frac{366}{365}\) vezes po dia terrestre, pelo que:

\(\omega_T\approx\frac{2\pi}{24\times3600}\times\frac{366}{365}s^{-1}\approx 7.3 \times 10^{-5} \ s^{-1}\)