Como se justifica esta rotação do plano do pêndulo? Para um observador terrestre, somos obrigados a considerar as forças inerciais e, destas, a única que aqui importa é a força de Coriolis ¹:

\(\vec{F}_c=-2m \ \vec{\omega}_T \ \times \vec{v}\)

FIGURA 1. A- Léon Foucault selo comemorativo. B- Pêndulo de Foucault no Pantheón de Paris.

onde \(\vec{\omega}_T\) é o vetor rotação instantânea da Terra. Vemos já, embora qualitativamente, que o plano de oscilação de um pêndulo não é mais invariante: a força de Coriolis, perpendicular à velocidade, obriga este plano a rodar.

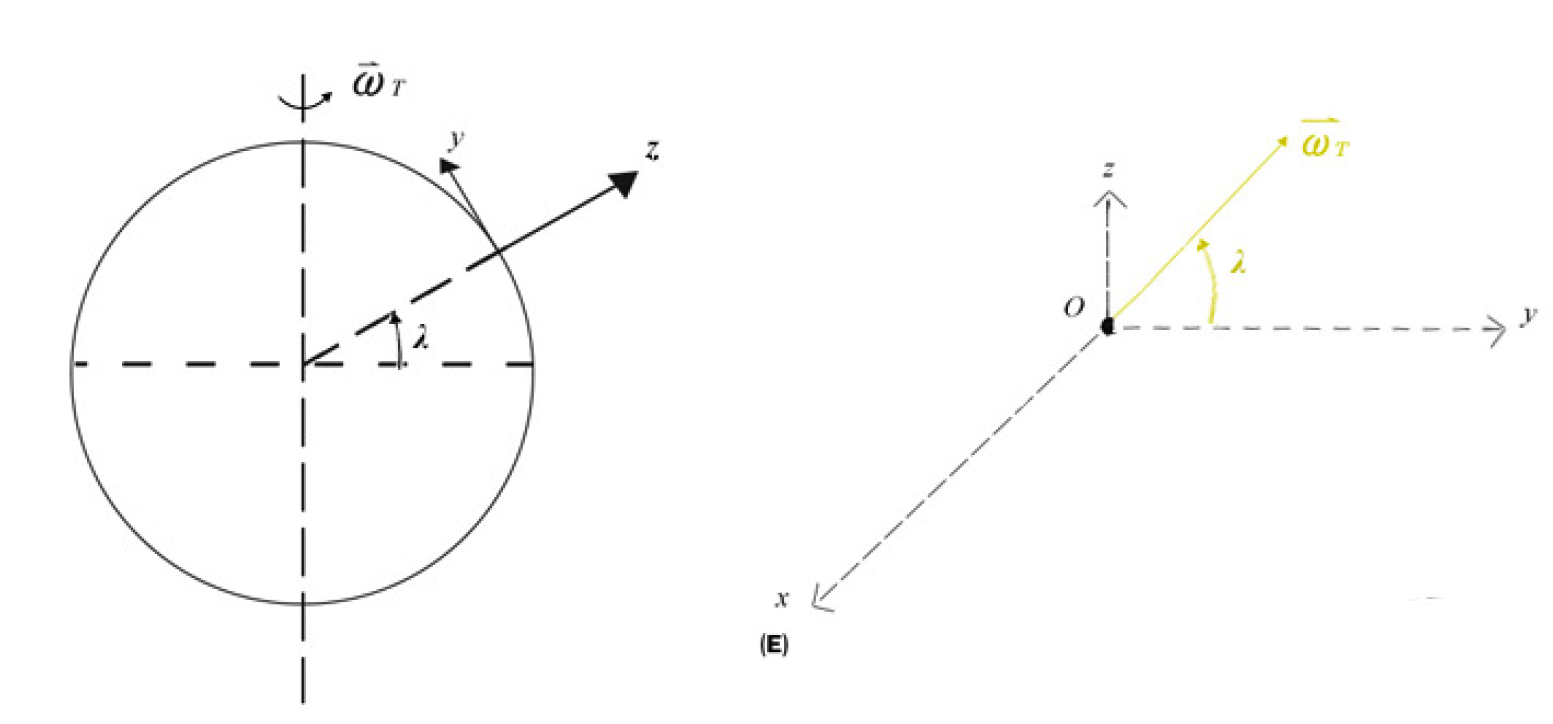
Procedamos à análise quantitativa, um pouco simplificada, considerando o caso habitual de pequenas oscilações, o que nos irá garantir que o fio permanece tenso. Nestas condições, o movimento do pêndulo situa-se, praticamente, no plano horizontal, onde escolhemos eixos \(x\), tangente o paralelo dirigido para Este, e \(y\), tangente ao meridiano dirigido para Norte (FIGURA 2). São ambos, evidentemente, perpendiculares entre si e também perpendiculares ao eixo vertical z. Será evidente que apenas a componente vertical de \(\vec{\omega}_T\), é responsável pela rotação do plano de oscilação. Se não houvesse a força de Coriolis, o movimento do pêndulo seria o de um oscilador harmónico, como se viu noutra publicação, o que significa que estaria, apenas, submetido à força \(-m\omega_0^2\vec{r}\), onde \(\omega _0-{\sqrt {g/l}} \) sendo \(l\) o comprimento do pêndulo. Pela consideração anterior, a força de Coriolis fica reduzida ao termo \(-2m\omega_t \ sen\lambda \ \vec{e_z}\times\vec{v}\), onde \(\lambda\) é a latitude do lugar. Assim, as equações de movimento no plano horizontal, são:

\(m\frac{d^2x}{dt^2}=-m\omega_0^2x+2m\omega_T \ sen\lambda\frac{dy}{dt}\)

\(m\frac{d^2y}{dt^2}=-m\omega_0^2y+2m\omega_T \ sen\lambda\frac{dx}{dt}\)

É útil, aqui, introduzir o complexo \(w = x + iy\). obtém-se:

\(\frac{d^2w}{dt^2}+\omega_0^2w+2i\omega_T \ sen\lambda\frac{dw}{dt}=0\)

É uma equação linear, pelo que se procuram soluções da forma \(w \sim e^{i\omega t}\), vindo:

\(-\omega^2+\omega_0^2-2\omega \ \omega_T \ sen\lambda= 0\)

Na situação habitual, é \(\omega_0 \gg \omega_T\), resultando:

\(\omega = \mp \ \omega_0-\omega_T \ sen\lambda\)

Deste modo, a solução geral para \(w(t)\) é:

\(w(t) =e^{-it\omega_T \ sen\lambda}(A e^{-it\omega_0}+Be^{-it\omega_0})\)

onde \(A\) e \(B\) são constantes, complexas, determinadas pelas condições iniciais. Suponhamos, então, que estas condições são \(w(0)=w_0\equiv a+ib\) e \(\dot{w}(0)=0\), isto é, o pêndulo é largado na posição genérica \(x = a\) e \(y = b\), com velocidade nula. obtém-se, assim:

\(A=\frac{\omega_0+\omega_T\ sen\lambda}{2\omega_0}\cong\frac{1}{2}\ \ \ \ \ B= \frac{\omega_0-\omega_T\ sen\lambda}{2\omega_0}\cong\frac{1}{2}\)

Substituindo na expressão anterior para \(w(t)\), resulta:

\(w(t) =e^{-it\omega_T \ sen\lambda} \ w_0 \ cos (\omega_0t)\)

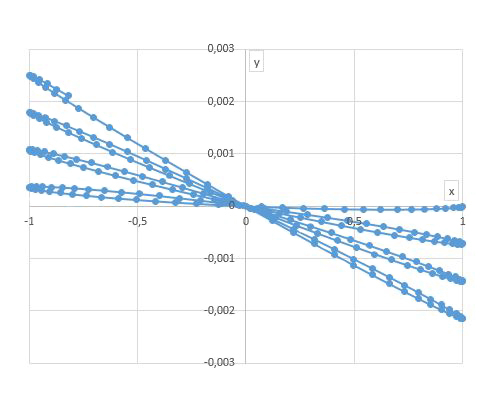
Se \(\omega_T=0\), este complexo tem sempre a direção de \(w_0\), i.e, a trajetória seria sempre um segmento de reta, o que corresponde ao plano invariante do pêndulo. Mas com \(\omega_T>0\), a fase do complexo cresce linearmente no tempo, i.e., a trajetória roda, no sentido contrário ao dos ponteiros de um relógio, o que corresponde à rotação do plano do pêndulo, como se mostra na FIGURA 3.

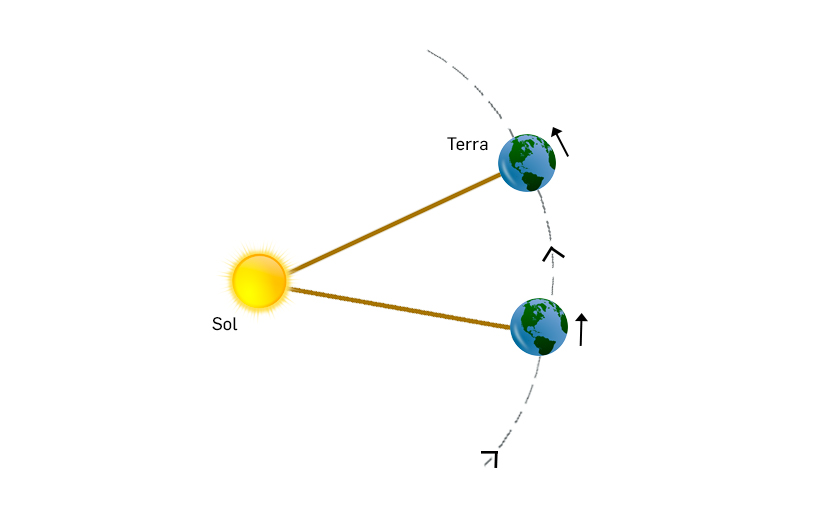
Tem interesse, neste contexto, analisar o valor de \(ω_T\). Como a Terra efetua uma rotação completa em 24h, poder-se-ia pensar que \(ω_T\approx\frac{2\pi}{24\times3600}s^{-1}\).Mas não é assim! Com efeito, um dia, i.e., 24 h é o tempo que decorre, para um observador na Terra, para o mesmo ponto do planeta se encontrar alinhado com o Sol. Mas, durante esse tempo, a Terra também se deslocou no seu movimento de translação em torno do Sol, que também é uma rotação. Para simplificar, aceitemos que este movimento é circular uniforme, realizando-se no mesmo sentido que a rotação da Terra (FIGURA 4). Então, ao fim de 24 h, a Terra rodou um pouco mais que \(2\pi\) e este excesso acumula-se exatamente em \(2\pi\) ao fim de um ano, quando a Terra regressa à sua posição inicial. Quer dizer, para um observador no Sol, considerado como observador inercial para quem \(\omega_T\) é definido, a Terra rodou 366 vezes no tempo correspondente a 365 dias terrestres, i.e., \(\frac{366}{365}\) vezes po dia terrestre, pelo que:

\(\omega_T\approx\frac{2\pi}{24\times3600}\times\frac{366}{365}s^{-1}\approx 7.3 \times 10^{-5} \ s^{-1}\)

¹ Com efeito, a rotação da Terra pode ser considerada uniforme e com eixo fixo em escalas de tempo da ordem de milhares de anos; os outros termos das forças inerciais, exceto Coriolis) adicionam a força centrífuga à força da gravidade, originando a definição de \(\vec{g}\) e a sua dependência na latitude.