Fluidos
📧
- Universidade do Porto
Referência Lage, E., (2018) Fluidos, Rev. Ciência Elem., V6(4):071
DOI http://doi.org/10.24927/rce2018.071
Palavras-chave Fluidos; líquidos; física; substância;
Resumo
Embora na linguagem mais comum o termo fluido seja usado como sinónimo de líquido, em física um fluido é uma substância que se deforma continuamente (ou flui) quando se aplica uma força (ou tensão) tangencial. Os fluidos mais comuns são os líquidos e os gases, mas há outros tipos de substâncias que também pertencem a esta categoria como é o caso dos plasmas e da lava de um vulcão.
Gases e líquidos, conjuntamente designados por fluidos, parecem diferir, apenas, na densidade (número de moléculas por unidade de volume): menor, para gases, maior para líquidos. Mas as diferenças nos arranjos moleculares são profundas e têm consequências macroscópicas. A energia de interação entre duas moléculas é, tipicamente, muito repulsiva a curtas distâncias (da ordem do tamanho da molécula), passando a atrativa para maiores distâncias, anulando-se para distâncias da ordem de três ou quatro diâmetros moleculares (alcance da interação).
Para fracas densidades, a distância típica entre moléculas é grande em relação ao alcance, as moléculas raramente interagem, podendo, até, ignorar-se esta interação (gás perfeito) - perante tal rarefação, não surpreende que o gás seja facilmente comprimível. A pressão que o gás exerce nas paredes do recipiente resulta das inúmeras colisões que, em cada segundo, moléculas efetuam com a parede; a velocidade da molécula, no momento da colisão, é da ordem da velocidade média que apresenta no interior do gás (velocidade térmica); daqui resulta que a pressão é simplesmente o produto da densidade pela temperatura absoluta: é a equação de estado do gás perfeito. Se um diafragma vibrar no seio do gás, ele empurra as moléculas que lhe estão mais próximas, tendo estas que se deslocar, com a velocidade térmica, até colidir com moléculas mais afastadas e estas, por sua vez, irão propagar, da mesma forma, o empurrão inicial: por isso, o som propaga-se, num gás, com uma velocidade da ordem da velocidade térmica. A velocidade do som no ar, em condições normais de pressão e temperatura é cerca de 340 m/s e, na água, nas mesmas condições, anda perto de 1000 m/s. A diferença deve-se à muito menor compressibilidade da água.
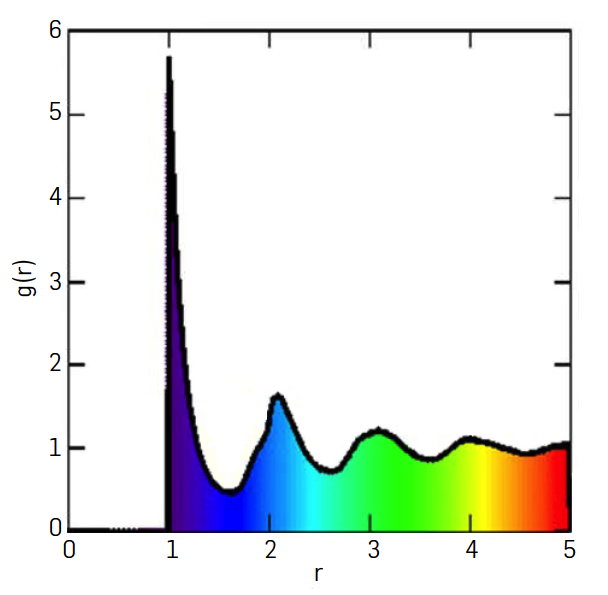
Aumentando a densidade, o efeito da parte atrativa da interação faz-se sentir: a molécula que esbarra na parede tem a maior parte das outras moléculas “atrás de si”, puxando-a: a velocidade no momento do choque é menor que a velocidade térmica – a pressão é inferior à do gás perfeito, é alterada a equação de estado como discutido em “pressão de vapor“. No seio do fluido real e à medida que aumenta a densidade, cada molécula “vê” mais moléculas dentro do alcance do potencial, criando-se pequenos arranjos locais de moléculas que crescem e persistem no tempo tanto mais quanto menor a temperatura, porque menor a agitação térmica.
Abaixo de uma certa temperatura, esses arranjos estendem-se a todo o fluido e este condensa – no líquido, cada molécula quer ter o maior número de moléculas dentro do alcance, mas este número está limitado pela parte repulsiva do potencial. É esta repulsão que determina, essencialmente, a densidade do líquido e a sua estrutura local: por isso, um líquido é quase incompressível. Se quiser empurrar as moléculas, elas quase não têm que se deslocar até empurrar as seguintes: a velocidade do som, num líquido, é muito maior que num gás. Gases nobres (do hélio ao radão) também condensam: o hélio condensa a 4,22 K (ou -268,93 ºC) e o seu ponto crítico tem temperatura crítica 5,19 K e pressão crítica 2,24 atm.
A parte atrativa da interação também tem importância num líquido: numa gota, as moléculas junto da superfície só são puxadas pelas do interior, daqui resultando a tensão superficial que tende a tornar a gota tão compacta quanto possível, isto é, com a forma esférica. É a tensão superficial que une os grãos de areia molhada, permitindo que caminhe mais facilmente na parte húmida do areal. E se quero vaporizar a gota à temperatura de ebulição, todo o calor fornecido serve, unicamente, para romper as ligações atrativas (calor latente).
Mas se a temperatura for muito elevada, determinando uma grande velocidade térmica, as forças atrativas não são suficientes para garantir a formação de estruturas persistentes: acima da temperatura crítica não é possível condensar um fluido, por maior que seja a pressão exercida.

Fluidos em movimento apresentam viscosidade, uma forma de atrito interno. (A exceção é o hélio superfluido). Se aplicarmos uma tensão tangencial a um sólido, ele deforma-se até atingir novo equilíbrio. Num líquido, porém, uma tensão tangencial origina escoamento, sendo válida, para muitos fluidos, a equação postulada por Newton:
\( \tau = \eta\frac{dv_x}{dy} \)
onde \(τ\) é a tensão exercida sobre uma camada de fluido, aqui suposta a mover-se segundo \(x\), pela camada adjacente (maior \(y\) ), e \(η\) é o coeficiente de viscosidade dinâmico. É, também, comum usar-se, para fluidos que se possam considerar incompressíveis, a viscosidade cinemática (unidades: m2/s no SI, ou stoke (St), no sistema CGS) \(v=\frac{\eta}{\rho}\), onde ρ é a massa específica. Todos os fluidos são, evidentemente, compressíveis. Porém, podem considerar-se incompressíveis (i.e., massa específica constante) se a velocidade do fluido for muito menor que a velocidade do som no seio desse fluido.
Deve observar-se que a viscosidade depende, em geral, da temperatura e pressão: aumentando a temperatura, diminui nos líquidos e aumenta nos gases ou vapores. A interpretação microscópica deste resultado é feita noutro artigo.
| Água | 1,000 |
| Azeite | 84 |
| Benzeno | 0,647 |
| Óleo de parafina | 103 |
| Vidro fundido | 1015 |
| Ar | 18,3x10-3 |
| Hélio | 18,6x10-3 |
| Metano | 10,3x10-3 |
| Vapor de água | 8,7x10-3 |
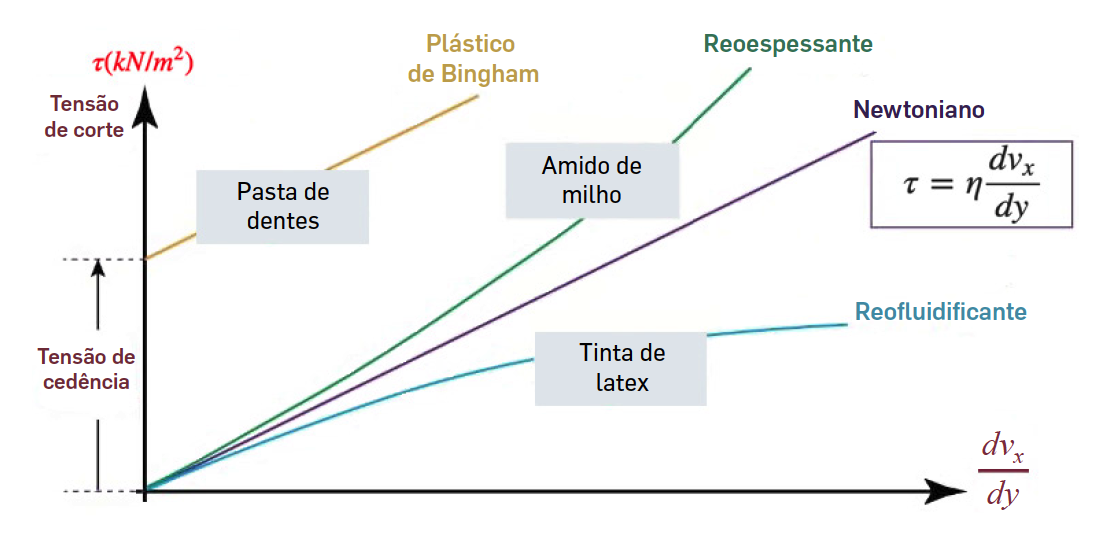
Os fluidos que obedecem à lei anterior designam-se por fluidos newtonianos. Mas há muitos outros exemplos onde a relação entre tensão aplicada e taxa de deformação não segue uma lei linear (FIGURA 3). Nestes, a tensão depende não linearmente da taxa de deformação ou mesmo a sua “história” - tal acontece com várias soluções salinas, mel, sangue, champô ou pastas dentífricas, etc., não sendo, pois, útil o conceito de coeficiente de viscosidade, sendo caracterizados por outros parâmetros reológicos. Contudo, em todos os casos, existe um atrito interno e, consequentemente, haverá produção de calor, manifestando irreversibilidade macroscópica: qualquer fluido, abandonado a si mesmo, acabará por atingir uma situação de equilíbrio onde nenhuma das suas partes (macroscópicas) se movimenta em relação a qualquer outra.
Esta breve introdução não pode deixar de referir o vastíssimo leque de comportamentos que vão da meteorologia à oceanografia, da acústica à turbulência, dos solitões em rios aos tsunamis, do pingo da torneira à bolha de sabão, e estende-se, mais recentemente, ao estudo de atmosferas e circulação de fluidos em exoplanetas sob condições extremas de pressões ou temperaturas. Mesmo o recurso aos mais potentes computadores para simulações numéricas é, muitas vezes, frustrado pelo fenómeno do caos caracterizado por um afastamento exponencial de soluções originadas por condições iniciais muito próximas. Compreende-se, assim, que os progressos, nos problemas mais complicados, surjam de aproximações mais ou menos justificadas pela definição de números adimensionais, como os números de Reynolds, Prandtl, Mach, Froude, Rayleigh, Taylor, etc., os quais medem a importância relativa de vários termos nas equações fundamentais, servindo, portanto, de guias para simplificações dessas mesmas equações. Alguns destes tópicos serão considerados em futuras publicações.
Este artigo já foi visualizado 9370 vezes.



