Ângulos e rotações

Se o ponto descreve um quarto de volta, o ângulo (de rotação) será igual a \(\displaystyle\frac{1}{4}\times 360º=90º\). Um outro exemplo, \(300º\) representa o valor do ângulo correspondente à rotação positiva de P de \(\displaystyle\frac{300}{360}= \displaystyle\frac{15}{18}\) de volta inteira.

Quando \(P\) roda no sentido negativo (horário), os ângulos são negativos.

Não há qualquer razão matemática para que uma volta inteira corresponda a \(360º\), ou, de outra forma, para que a unidade de medida seja o grau = \(\displaystyle\frac{1}{360}\) de volta inteira. De facto a única razão é de carácter histórico - é assim desde a antiguidade clássica. Como veremos, existe uma unidade de medida mais apropriada do ponto de vista matemático - o radiano.

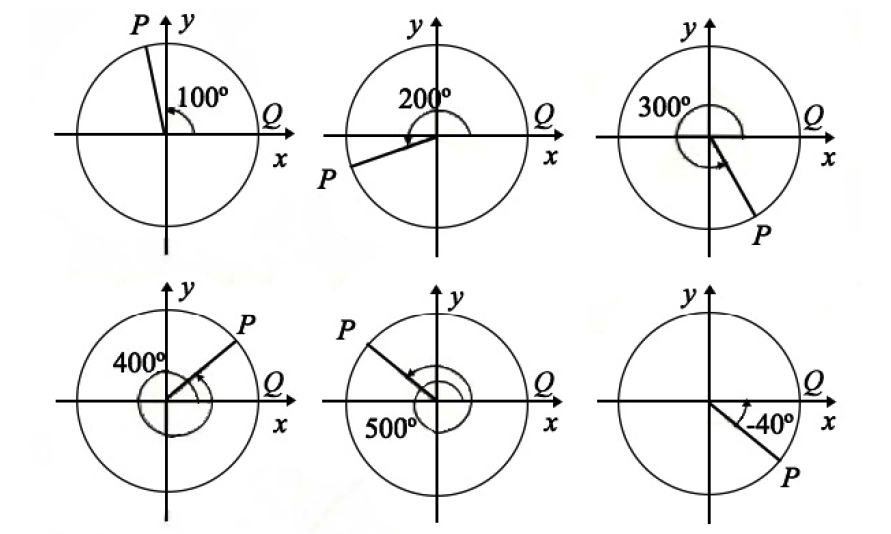
Mas o que significa um ângulo (de rotação) de \(500º\)? Como \(5800º=360º+140º\), significa que o ponto P deu uma volta inteira, no sentido positivo, a que correspondem \(360º\), e depois continuou a rodar descrevendo um ângulo (de rotação) correspondente à rotação positiva de \(P\) de \(\displaystyle\frac{140}{360}= \displaystyle\frac{7}{18}\) de volta inteira (veja a figura).

Podemos pois definir ângulos de rotação, ou mais simplesmente, ângulos de qualquer valor, racional ou irracional, positivo ou negativo, medidos em graus.

Ângulos orientados

Noção de ângulo

Uma semi-reta de origem \(O\), pertencente a um dado plano, pode mover-se nesse plano rodando em torno de \(O\) em dois sentidos: ou no sentido contrário ao do movimento dos ponteiros do relógio que será o sentido positivo, ou no sentido oposto, sentido negativo.

Quando a semi-reta partindo da posição \(a\), roda em torno da origem \(O\) acabando por ocupar a posição \(b\), diz-se que descreveu o ângulo \(\angle a,b\). À semi-reta \(a\) chamamos lado origem e à semi-reta \(b\) lado extremidade. O ponto \(O\) é o vértice do ângulo.

Assim, o ângulo é positivo ou negativo, conforme o sentido de rotação que leva o lado origem a ocupar a posição lado extremidade seja positivo ou negativo. Nestas condições, a ordem pela qual se consideram lados do ângulo não é indiferente tendo o ângulo um sentido (ângulo orientado).

Quando a semirreta a descreve uma rotação em torno da origem O de tal forma que vem a ocupar a posição inicial, efetuando assim uma revolução completa num dado sentido, dizemos que essa semirreta descreveu o ângulo de um giro, ou mais simplesmente, um ângulo giro. E como nada impede que esse movimento de rotação continue (no sentido positivo ou negativo), concebem-se assim ângulos (positivos ou negativos) que podem exceder um ou mais ângulos giros.

Portanto, um par ordenado (a,b) de duas semirretas com a mesma origem O corresponde a um ser geométrico múltiplo chamado ângulo trigonométrico, constituído por um número infinito de determinações, cada uma das quais se refere à amplitude e sentido da rotação que leva o lado origem a coincidir com o lado extremidade.

Medida dos ângulos

Se \(A\) e \(U\) forem duas grandezas (da mesma espécie contínua) e se \(U\) for não nula, existe um e um só número real \(\alpha\) tal que, \(A=\alpha U\). A este número \(\alpha\) chama-se a medida de \(A\) relativamente a \(U\). Determinar \(\alpha\) é medir a grandeza \(A\) tomando para unidade a grandeza \(U\).

Considerando agora os ângulos orientados, podemos afirmar que dadas duas determinações \(A\) e \(U\), (\(U\) não nulo), de dois ângulos, existe um e um só número real \(m\) tal que, \(A=m U\). O número \(m\) representa assim a medida da determinação do ângulo \(A\) relativamente à unidade \(U\).

Fixada a unidade \(U\) estabelece-se assim uma correspondência biunívoca entre o conjunto dos ângulos orientados e conjunto dos números reais (medidas dos ângulos). Esta correspondência é tal que a relação de igualdade, a relação de grandeza e a adição de ângulos se traduz, respetivamente, na relação de igualdade, na relação de grandeza e na adição de números reais.

A escolha da unidade \(U\) é arbitrária, mas habitualmente usa-se um dos três sistemas de unidades definidos em seguida.

Sistema sexagesimal

No sistema sexagesimal admite-se como unidade fundamental o grau. Um grau corresponde a \(\displaystyle \frac{1}{90}\) do ângulo reto que por sua vez é um quarto de um ângulo giro.

Assim sendo, um ângulo reto mede \(90º\) (90 graus) e um ângulo giro mede \(360º\) (360 graus) pois \(90\times4=360\).

Como submúltiplos do grau usam-se:

O minuto sexagesimal \((1')\) corresponde a \(\displaystyle \frac{1}{60}\) do grau, ou seja, 60 minutos sexagesimais são 1 grau.

O segundo sexagesimal \((1' ')\) corresponde a \(\displaystyle \frac{1}{60}\) do minuto e portanto \(\displaystyle \frac{1}{3600}\) do grau, ou seja, 3600 segundos sexagesimais são 1 grau.

O décimo do segundo, o centésimo do segundo etc.

Submúltiplos do grau	Um grau
Minutos	60
Segundos	3600
Décimos de segundo	36000
Centésimos do segundo	360000
\(\dots\)	\(\dots\)

Exemplo

Um ângulo composto de 30 graus, 12 minutos, 8 segundos e 2 centésimos que simbolicamente podemos representar por \(30º\) \(12'\) \(8' '\) \(,02\) tem uma medida em graus de \(\displaystyle 30+\frac{12}{60}+\frac{8}{3600}+\frac{2}{360\times 100} \simeq 30,2023\).

Para indicar a medida deste ângulo usamos habitualmente a notação \(30º\) \(12'\) \(8' '\) \(,02\) para nos referirmos ao número anterior.

Sistema centesimal

No sistema centesimal admite-se como unidade fundamental o grado. Um grado corresponde a \(\displaystyle \frac{1}{100}\) do ângulo reto que por sua vez é um quarto de um ângulo giro.

Assim sendo, um ângulo reto mede \(100^{g}\) (100 grados) e um ângulo giro mede \(400^{g}\) (400 grados) pois \(100\times4=400\).

Como submúltiplos do grado usam-se:

O minuto centesimal \((1^{‵})\) corresponde a \(\displaystyle \frac{1}{100}\) do grau, ou seja, 100 minutos centesimais são 1 grado.

O segundo centesimal \((1‶)\) corresponde a \(\displaystyle \frac{1}{100}\) do minuto e portanto \(\displaystyle \frac{1}{10000}\) do grado, ou seja, 10000 segundos centesimais são 1 grado.

O décimo do segundo centesimal, o centésimo do segundo centesimal etc.

Submúltiplos do grado	Um grado
Minutos	100
Segundos	10000
Décimos de segundo centesimal	100000
Centésimos do segundo centesimal	1000000
\(\dots\)	\(\dots\)

Exemplo

Um ângulo composto de 20 grados, 8 minutos e 24 segundos que simbolicamente podemos representar por \(20^{g}\) \(8^{‵}\) \(24‶\) tem uma medida em grados de \(\displaystyle 20+\frac{8}{100}+\frac{24}{10000}=20,0824\).

Para indicar a medida deste ângulo no sistema centesimal usamos habitualmente a notação \(20^{g}\) \(8^{‵}\) \(24‶\) para nos referirmos ao número anterior.

Sistema circular

No sistema circular a unidade de medida é o radiano. Como sabemos um radiano é a medida de um ângulo ao centro definido num círculo por um arco com o mesmo comprimento que o raio do círculo. Sabemos também que existe proporcionalidade direta entre a medida de um ângulo ao centro e o comprimento do arco correspondente. Considerando o ângulo da FIGURA 1 podemos então estabelecer que:

\[\frac{\mbox{medida de um radiano}}{\mbox{medida de um ângulo giro}}=\frac{\mbox{comprimento do arco } AB}{\mbox{comprimento da circunferência}}\]

Como o comprimento do arco \(AB\) é igual ao raio do círculo, resulta que

\[\frac{\mbox{medida de um radiano}}{\mbox{medida de um ângulo giro}}=\frac{r}{2\pi r}=\frac{1}{2\pi}\]

Esta relação mostra que a medida de um ângulo giro é de \(2\pi\) radianos. Estabelecendo a relação com os dois sistemas de unidades anteriores temos que:

\(360º=2\pi \mbox{ radianos}\) e \(400^{g}=2\pi \mbox{ radianos}\)

Daqui resulta que,

\(\displaystyle 1 \mbox{ radiano}={\left(\frac{360}{2\pi}\right)}^{\circ} \simeq \, 57º \,\, 17' \,\, 45' '\)

\(\displaystyle 1 \mbox{ radiano}=\left(\frac{400}{2\pi}\right)^{g} \simeq \, 63,6620^g \)

Passagem de um sistema de unidades para outro

Consideremos um ângulo \(\angle a,b\) qualquer e designemos por \(s\), \(c\) e \(d\) as suas medidas nos sistemas sexagesinal, centesimal e circular, respetivamente. Necessitamos de estabelecer uma relação destas medidas com medidas já conhecidas, como por exemplo, a medida de um ângulo raso, que é de \(180º\) no sistema sexagesimal, de \(200^{g}\) no centesimal e de \(\pi \mbox{ rad}\) no circular. Como a razão entre grandezas da mesma espécie é o quociente das suas medidas relativamente a uma unidade comum, resulta que a razão entre o ângulo \(\angle a,b\) e o ângulo raso pode ser expressa pelos números \(\displaystyle \frac{s}{180}\), \(\displaystyle \frac{c}{200}\) ou por \(\displaystyle \frac{d}{\pi}\).

Como os três números anteriores são iguais então temos que:

\(\quad \frac{s}{180}=\frac{c}{200}=\frac{d}{\pi} \quad\)

Esta relação permite-nos, conhecendo a medida de um ângulo num dos sistemas, determinar a medida desse mesmo ângulo num dos outros dois sistemas de unidades.

Exemplo

Cálculo das medidas do ângulo \(28º\) \(48'\) nos sistemas centesimal e circular.

Usando a relação anterior temos que \(s=28,8\) pois \(48'=0,8º\),então

\(\displaystyle \frac{28,8}{180}=\frac{c}{200} \, \Leftrightarrow \, c=\frac{200 \times 28,8}{180}=32\)

Da mesma forma determinamos a medida do ângulo no sistema circular:

\(\displaystyle \frac{28,8}{180}=\frac{d}{\pi} \, \Leftrightarrow \, d=\frac{\pi \times 28,8}{180}=\frac{28,8}{180}\pi=\frac{4}{25}\pi \simeq 0,503\)

Logo, o ângulo \(28º\) \(48'\) mede \(32^{g}\) no sistema centesimal e aproximadamente \(0,503 \mbox{ rad}\) no sistema circular.

Notas históricas

Dos três sistemas de unidade descritos anteriormente é o sistema circular que parece suscitar maior interesse teórico pela quantidade de assuntos matemáticos em que intervém. Já os outros dois sistemas, sistema sexagesimal e sistema centesimal, são mais utilizados nas aplicações práticas mais elementares.

O sistema sexagesimal será, dos três sistemas de unidades, o mais antigo, como podemos ler na Enciclopédia das Matemáticas Elementares (Berzolari, Milão, 1937, Vol.II p.545), «O sistema sexagesimal é de origem remotíssima. Os Babilónios dividiam a circunferência em 360 partes iguais e esta subdivisão transmitiu-se aos Gregos e Árabes e chegou até nós».

O sistema centesimal parece datar do séc.XV. O notável geómetra H.Briggs (1556-1630) utilizou a subdivisão centesimal na construção duma tábua trigonométrica. Mais tarde, o matemático francês J.L.Lagrange (1736-1813) mostrou-se defensor da substituição do sistema sexagesimal pelo sistema centesimal de unidades de medida de ângulo. Apesar do sistema centesimal ser mais cómodo a nível de cálculo, uma vez que se usam medidas expressas em números decimais, ainda hoje podemos verificar que o sistema mais utilizado e mais comum é o sistema sexagesimal.