Qual a equação cartesiana desta recta?

Como se sabe da geometria analítica plana, a equação da recta que une os pontos A e B é:

\(\displaystyle y-f(a)=\frac{f(a+h)}{(a+h)-a}(x-a)\)

ou:

\(\displaystyle y=f(a)+ \Delta_af(h)\, (x-a)\)

Portanto o declive desta recta, isto é, a tangente do ângulo positivo que esta recta faz com a parte positiva do eixo dos xx, é igual à taxa média de variação de f em a.

Qual a posição limite desta recta quando \(\displaystyle h\to 0\)?

Quando \(\displaystyle h\to 0\) a taxa média de variação de f em a, \(\displaystyle \Delta_af\),converge para a taxa instantânea de variação de f em a, isto é, converge para a derivada f'(a) de f em a (supondo que esta existe).

Portanto a recta que une A e B tem uma posição limite que não é mais do que a recta tangente ao gráfico de f no ponto \(\displaystyle A=(a,f(a))\). A respectiva equação é obtida a partir da equação anterior em , fazendo \(\displaystyle h\to 0\):

\(\displaystyle y=f(a)+ f'(a) (x-a)\)

O declive da recta tangente ao gráfico de f no ponto \(\displaystyle A=(a,f(a))\), é pois igual à derivada \(\displaystyle f'(a)\) de f em a.

Considere ainda os pontos seguintes:

\(\displaystyle B=(a+h,f(a+h))\), no gráfico de f e \(\displaystyle B'=(a+h,f(a)+f'(a)\,h)\), na recta tangente ao gráfico de f no ponto \(\displaystyle A(a,f(a))\)

A diferença das ordenadas destes dois pontos é igual a:

\(\displaystyle f(a+h)- [f(a)+f'(a)\,h]\)

e esta diferença é cada vez mais pequena quanto mais próximo de 0 estiver o "acréscimo" h. Neste sentido podemos pois dizer que o valor exacto 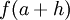é aproximadamente igual a \(\displaystyle f(a)+f'(a)\,h\), sendo esta aproximação cada vez mais precisa quanto mais pequeno é o valor de h:

\(\displaystyle f(a+h) \approx f(a)+ f'(a)h\)

Mais concretamente: se definirmos o erro \(\displaystyle e(a;h)\) através da diferença:

\(\displaystyle e(a;h) \doteq f(a+h)- [f(a)+ f'(a)h ]\)

podemos dizer que:

\(\displaystyle \lim_{h\to 0} \frac{e(a;h)}{h}=0\)

Diz-se então que o erro \(\displaystyle e(a;h)\) é um infinitésimo de ordem superior a h.

A diferencial da função f no ponto a, é a função \(\displaystyle df_a:\mathbb{R}\longrightarrow \mathbb{R}\) que a cada acréscimo \(\displaystyle h \in \mathbb{R}\) associa o valor

\(\displaystyle df_a\doteq f'(a)\cdot h\). É pois uma função linear em \(\displaystyle h\) - de facto a função linear que melhor aproxima f em a, no sentido em que:

\(\displaystyle \lim_{h\to 0} \frac {(f(a+h)-f(a))- df_a(h)}{h}=0\)

que não é mais do que a versão formal do que se disse antes, e que se presta a generalização.