Equação de estado de van der Waals
📧
- Universidade do Porto
Referência Lage, E., (2019) Equação de estado de van der Waals, Rev. Ciência Elem., V7(1):005
DOI http://doi.org/10.24927/rce2019.005
Palavras-chave van der Waals;
Resumo
A equação de estado de van der Waals para um gás corrige as hipóteses básicas para a validade da equação de estado de um gás ideal, considerando que as partículas (átomos ou moléculas) ocupam um certo volume e que interatuam entre si de forma atrativa ou repulsiva. Daqui resulta uma equação de estado que pode ser interpretada como uma modificação da equação dos gases ideais para corrigir o volume acessível às partículas e corrigir a pressão pelo efeito das interações entre as partículas.
É bem conhecida a equação de estado de um gás ideal, a relação termodinâmica entre a pressão que o gás exerce, o volume que ocupa e a temperatura absoluta a que está submetido:
\(P=\frac{N}{V}kT\) (1)
Aqui, \(N\) é o número de partículas do gás e \(k\) é a constante de Boltzmann: \(k=\frac{R}{N_A}\), onde \(R\) é a constante dos gases perfeitos e \(N_A\) é o número de Avogadro. Esta equação, apresentada pela primeira vez por Émile Clapeyron, em 1834, integra os resultados empíricos anteriormente obtidos por Charles, Gay-Lussac e Avogadro e é ainda hoje muito usada como uma primeira abordagem no estudo de gases reais. Contudo, ela falha quando a interação entre as partículas (átomos ou moléculas) não puder ser ignorada (FIGURA 1), como acontece para elevadas densidades ou para baixas temperaturas, isto é, quando a distância média entre partículas vizinhas é inferior ao alcance da energia de interação entre elas (da ordem de 4 ou 5 vezes \(R_{min}\) ) ou quando a energia cinética média dessas partículas, determinada pela temperatura absoluta, é comparável com essa mesma energia de interação (da ordem de \(\mid𝜀_{min}\mid\)). Esta energia tem, certamente, que ser levada em consideração se quisermos descrever a condensação de um gás real.
Em 1873, Johannes Diderik van der Waals propôs uma nova equação de estado que já incorporava algumas das caraterísticas da energia de interação.
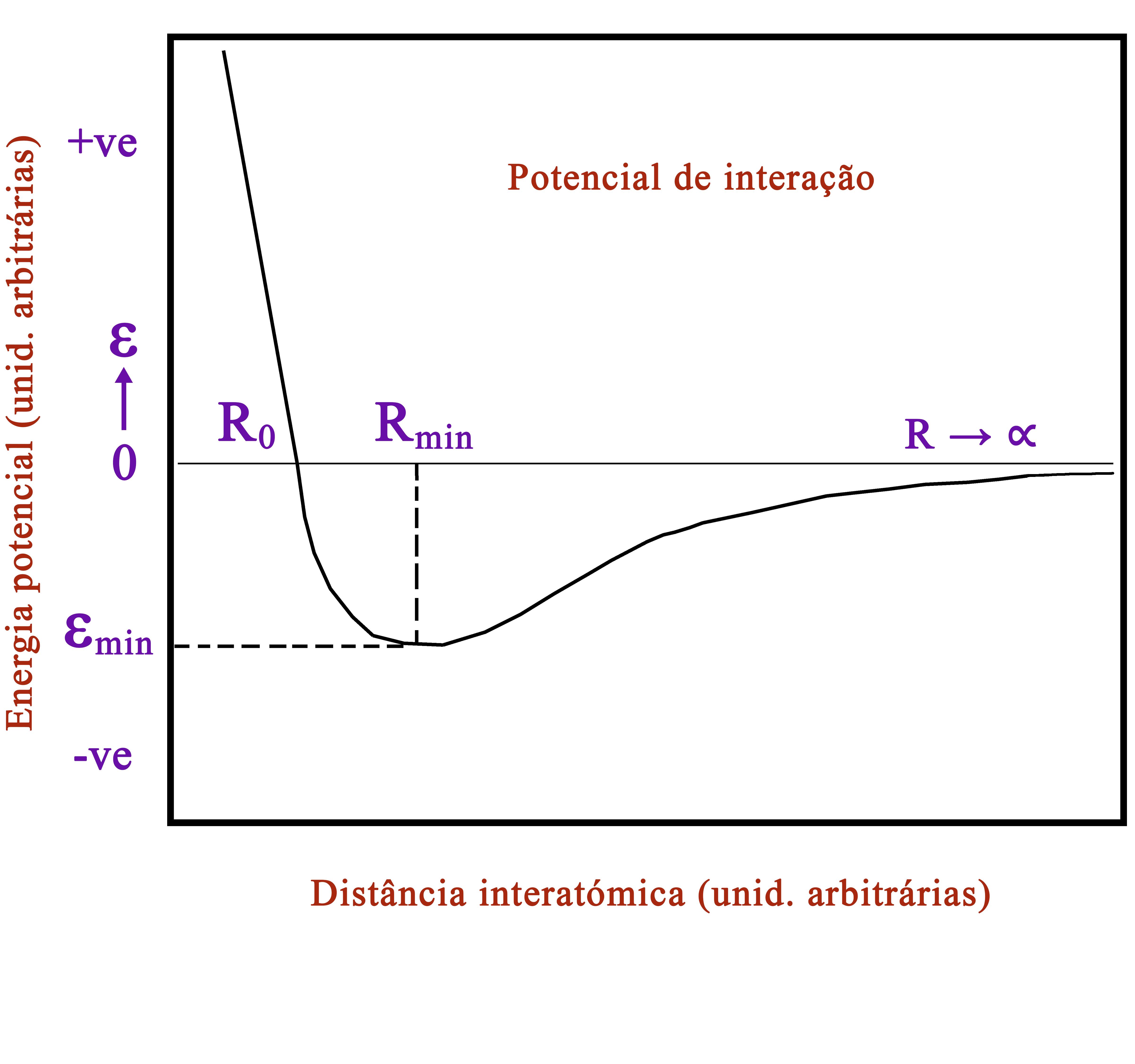
A primeira correção assenta na observação (FIGURA 1) que existe uma forte repulsão interatómica para distâncias, entre os seus núcleos, inferiores a \(R_0\) que pode, por isso, ser considerado uma estimativa do diâmetro atómico. Quer dizer, cada átomo exclui um volume, que designaremos por \(b\sim\frac{4\pi}{3}R_0^3\), de modo que as \(N\) partículas movem-se num volume efetivo da ordem de \(V − Nb\).

A segunda correção leva em conta a parte atrativa da energia de interação. Na teoria atómica, a pressão \(P\) de um gás ideal resulta das colisões, supostas elásticas, que, em cada segundo, as partículas efetuam com as paredes do recipiente. Ora, existindo aquela parte atrativa na interação, as partículas colidem com as paredes com uma velocidade média menor que no gás ideal porque são travadas pelas que se situam mais no interior. É, assim, de esperar que a pressão \(p\) de um gás real seja inferior à pressão \(P\) do gás ideal, sendo a diferença determinada pelo número de pares de partículas, umas na unidade de volume que irão colidir com a parede, outras na unidade de volume que puxam aquelas para o interior, i.e., \(p ≈ P − n^2 a\), onde \(n=\frac{N}{V}\) é o número de partículas por unidade de volume; e \(a\sim𝜀_{min}R_{min}^3\) deve ser considerada, tal como \(b\), uma grandeza fenomenológica.
Substituindo estas correções na equação de estado do gás perfeito, obtemos a equação de van der Waals:
\((p+an^2)(V-Nb)=NkT\) (2)
Esta equação de estado, apesar da sua simplicidade, apresenta um grande progresso em relação à equação dos gases perfeitos. A FIGURA 3 exibe as isotérmicas para várias temperaturas.
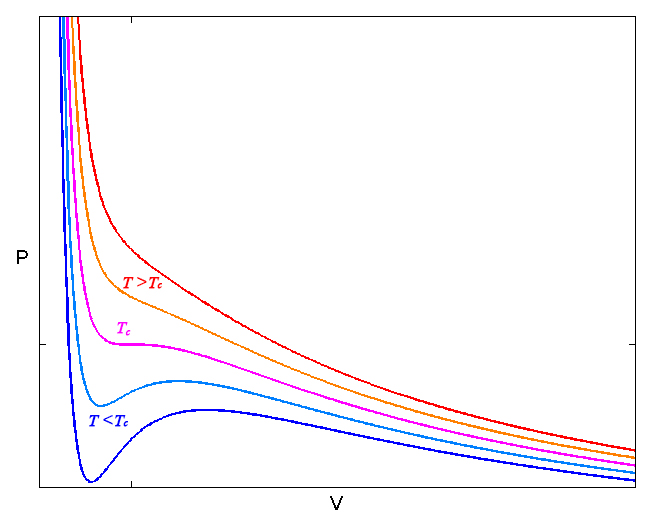
Vemos que, para altas temperaturas (conceito que se tornará preciso mais abaixo), as isotérmicas têm a forma hiperbólica como no gás ideal. Mas existe uma temperatura \(T_C\) que apresenta um ponto de inflexão, isto é, são nulas a primeira e a segunda derivadas:
\(\left(\frac{\partial p}{\partial V}\right)_{T_C,V_C}=\left(\frac{\partial^2 p}{\partial V^2}\right)_{T_C,V_C}=0\) (3)
Usando a equação de estado (2), é fácil encontrar:
\(kT_C=\frac{8a}{27b} \ \ \ \ \ \ \ V_C=3Nb \ \ \ \ \ \ \ p_C=\frac{a}{27b^2}\) (4)
A existência de um tal ponto crítico é bem conhecida em gases reais: acima de uma temperatura crítica \(T_C\), um gás não condensa, por maior que seja a pressão exercida!
Mas, que se passa abaixo desta temperatura crítica? Num gás real, há separação do fluido em duas fases, uma líquida e a outra vapor, coexistindo às mesmas temperatura e pressão. As isotérmicas de van der Waals não parecem descrever esta situação. Pior: abaixo da temperatura crítica, as isotérmicas apresentam regiões onde \(\frac{\partial p}{\partial V}>0\), uma clara violação da estabilidade termodinâmica. Uma solução \(ad hoc\) deste problema foi apresentada por Maxwell em 1875 e está exibida na FIGURA 4: na isotérmica, a porção \(adbec\) é substituída pelo segmento horizontal \(abc\) correspondente a uma pressão (\(P_V\) na figura) determinada pela exigência de igualdade das áreas sobre \(adb\) (azul) e \(sob bec\) (amarela). Porquê? Porque o trabalho extraído do ciclo \(adbecba\) deve ser nulo, conforme o exige a 2ª lei da Termodinâmica (não é possível obter trabalho a partir de uma fonte a temperatura uniforme), isto é, \(∮ dV p(V,T) = 0\) (integral sobre o ciclo referido) e este resultado não é mais do que a igualdade das áreas referidas. Com esta construção, a isotérmica passa a ter um patamar horizontal em \(P_V\), ficando determinado o equilíbrio do volume na fase líquida \(V_L\), de maior densidade, e do volume na fase de vapor \(V_G\).
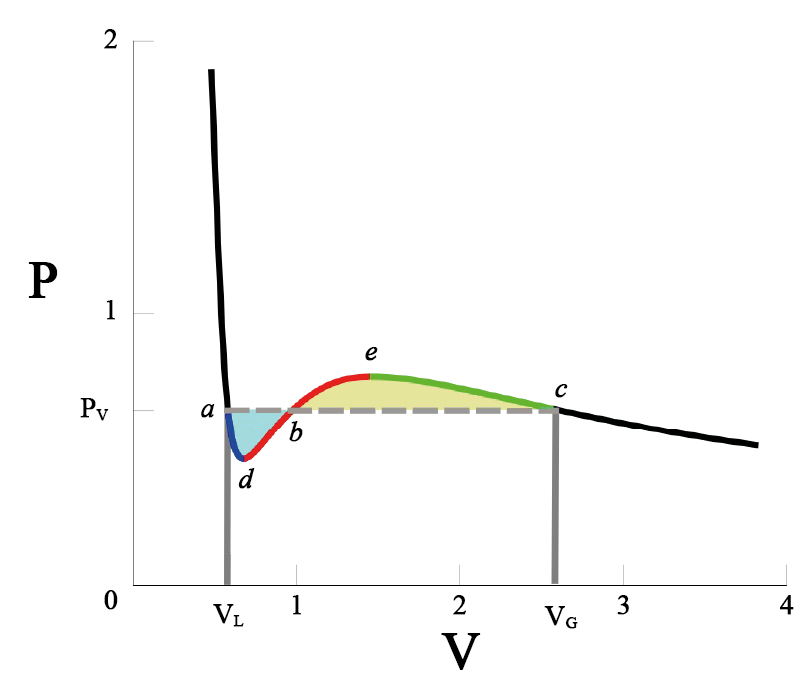
Adicionalmente, ficam, também, definidos os limites de estabilidade da fase líquida (ponto \(d\), na figura), correspondente a sobreaquecimento, e da fase de vapor (ponto \(e\)), correspondente a subarrefecimento (no caso, será preferível designa-los por sub-pressão e sobre-pressão, respetivamente).
Regressando à equação de van der Waals, podemos escrevê-la sob forma adimensional, o que elimina qualquer referência às constantes \(a\) e \(b\). Para tal, definimos \(V'\equiv\frac{V}{V_C},p'\equiv\frac{p}{p_C}\) e \(T'\equiv\frac{T}{T_C}\), obtendo-se:
\(p'=\frac{8T'}{3V'-1}-\frac{3}{V'2}\) (5)
Esta expressão é conhecida por lei dos estados de van der Waals correspondentes e ela sugere que um comportamento universal para todos os fluidos pode ser obtido representando adimensionalmente as variáveis de estado, recorrendo aos seus valores no ponto crítico, um resultado que transcende a própria equação de van der Waals e sobrevive na moderna teoria das transições de fase.
Mas também mostra uma outra limitação daquela equação de estado porque admite pressões negativas se \(T'<\frac{27}{32}\). Apesar disso, a equação de van der Waals não tem apenas valor histórico: ela representa um real progresso em relação à equação dos gases perfeitos e mostra claramente que é possível tratar transições de fase dentro dos princípios da Termodinâmica.
Referências
- 1 Atkins, P. & Paula, J., Physical chemistry, 8th Edn., pp. 17-22, 104f, 632-641, New York, NY, USA: Macmillan, 2006, ISBN 0716787598
- 2 Klein, M. J., The Historical Origins of the van der Waals Equation. Physica. 73 (1): 31, 1974.
- 3 Lebowitz, J., Exact derivation of the Van der Waals equation. Physica. 73, 48-60, 1974.
- 4 Robert. J. S. et al. Physical Chemistry (4th ed.). Wiley, 2004, ISBN 978-0471215042
Este artigo já foi visualizado 23038 vezes.



