Na Teoria da Relatividade Geral existem singularidades inerentes à teoria, como foi demonstrado por Stephen Hawking e Roger Penrose (para uma exposição detalhada ver por exemplo, “Large Scale Structure of Space Time” escrito em colaboração com o físico sul-africano George Ellis, publicado em 1973¹). Uma dessas singularidades corresponde ao início do Universo – Big Bang – , outras apresentam-se nos buracos negros. Estes podem ser estelares, que advêm do colapso gravitacional de uma estrela com pelo menos três massas solares, ou galáticos, supostamente no centros das galáxias e muito particularmente daquelas com o núcleo central ativo, ou ainda serem objetos mais exóticos - os buracos negros primordiais, formados da matéria inicial do Universo. Apesar de serem bastante bizarros, os buracos negros podem existir em profusão no Universo. De facto, há inúmeros indícios de que a maioria das galáxias alberga no seu centro um buraco negro supermaciço, sendo que a primeira imagem de um objeto desta natureza com uma massa de 6,5 mil milhões vezes a do Sol, residente no centro da galáxia M87 a 55 milhões de anos-luz da Terra, foi obtida pelo projeto Event Horizon Telescope e divulgada no dia 10 de abril de 2019.

A primeira solução exata das equações de campo de Einstein no vazio, descoberta por Karl Schwarzschild em 1916, descreve o espaço-tempo exterior a um buraco negro estático através do elemento de linha nas coordenadas de Schwarzschild³:

\(ds^2=-\left(1-\frac{r_{sc}}{r}\right)c^2dt^2+\left(1-\frac{r_{sc}}{r}\right)^{-1}dr^2+r^2dΩ\)

onde \(r_{sc}=2 GM⁄c^2\) é o raio de Schwarzschild que relaciona a constante da gravitação de Newton, G, a massa do buraco negro, M, e a velocidade da luz, c; \(dΩ=sin(θ)^2 dθ^2+dϕ^2\) é o elemento de ângulo sólido, escrito em coordenadas esféricas.

Outra solução exata refere-se aos buracos negros eletricamente carregados com carga, Q, e uma putativa carga magnética (monopolo magnético), P: os buracos negros de Reissner-Nordstrom:

\(ds^2=-\left(\frac{r^2-r_{sc}r+\overline{Q}^2}{r^2}\right) c^2 dt^2+\left(\frac{r^2dr^2}{r^2-r_{sc}r+\overline{Q}^2}\right)+r^2 dΩ,\)

em que \(\overline{Q}^2=G (Q^2+P^2 )⁄4 \piϵ_0 c^4\) com o fator \(1⁄4 \piϵ_0\) sendo a constante de Coulomb. Notemos ainda que quando é nula, a expressão \(\frac{r^2-r_{sc}r+\overline{Q}^2}{r^2}\) admite raízes reais distintas, reais degeneradas (ambas correspondendo a horizonte de eventos), ou complexas as quais se pensa não corresponderem a realidades físicas uma vez que a singularidade seria “nua”, não estando protegida causalmente por um horizonte de eventos e, como tal, violando a hipótese da censura cósmica de Roger Penrose. Assim, surge a condição \(2\overline{Q}< r_{sc}\).

Existem também os buracos negros de Kerr-Newman, os quais apresentam uma rotação, e correspondem à solução mais geral de buraco negro estacionário no contexto da Teoria da Relatividade Geral. O seu elemento de linha, em coordenadas de Boyer-Linquist, escreve-se como³:

\(ds^2=-\left(\frac{\Delta^2-a^2 sin(\theta)^2}{\Sigma}\right)c^2 dt^2-2asin(\theta)^2\frac{r^2+a^2-\Delta}{\Sigma}cdtd\phi+\frac{(r^2+a^2 )^2-\Delta a^2 sin(\theta)^2}{\Sigma}sin(\theta)^2d\phi^2+\frac{\Sigma}{\Delta}dr^2+\Sigma d\theta^2\)

onde \(\Delta =r^2-r_{sc} r+a^2+\overline{Q}^2\), sendo \(a=J⁄Mc\) a razão entre o momento angular e a massa do buraco negro, e \(\Sigma =r^2+a^2 cos(\theta)^2\). Notemos que se \(\overline{Q}=0\), então o buraco negro diz-se simplesmente de Kerr. De modo análogo ao caso anterior, surge a condição entre carga e momento angular \(\overline{Q}^2+a^2 < r_ {sc}^2⁄4\) para que não haja singularidades nuas.

Através da métrica e da Teoria Quântica de campos em espaços curvos podemos descrever a dinâmica dos buracos negros. É possível verificar que apresenta uma notável semelhança com as quatro leis conhecidas da termodinâmica. Um passo decisivo neste domínio foi dado por Stephen Hawking ao demonstrar que os buracos negros emitem radiação térmica e que no processo perdem massa por evaporação devido ao aumento das forças de maré responsáveis pela criação de pares partícula/antipartícula, sendo a temperatura dada por⁴:

\(T_H=\frac{ℏc^3}{8\pi k_B GM}\)

onde ℏ é a constante de Planck reduzida e \(k_B\) a constante de Boltzmann.

Podemos, pois, esquematizar a analogia entre as descrições dinâmica e termodinâmica dos buracos negros através do quadro seguinte^3,4:

	Mecânica de Buraco Negro	Termodinâmica
Lei Zero	O estado estacionário de um buraco negro é caraterizado pela gravidade de superfície \(κ=\frac{\sqrt{r_{sc}^2-4\overline{Q}^2-4a^2}}{r_{sc}^2-2\overline{Q}^2+r_{sc} \sqrt{r_{Sc}\ ^2-4\overline{Q}^2-4a^2}}\) , no seu horizonte. Esta é a aceleração que uma partícula em repouso sente perto do horizonte de eventos, medida por um observador no infinito.	O estado de equilíbrio térmico de um corpo é caraterizado pela sua temperatura, \(T\), constante.
Primeira Lei	A variação de energia (massa) de um buraco negro estacionário relaciona-se com as variações da sua área, \(A\), do seu momento angular, \(J\), e da sua carga elétrica, \(Q\), através de: \(\delta E=\frac{κ}{8\pi G} \delta A+\Omega c^2 \delta J+\Phi \delta Q\) onde \(Ω\) é a velocidade angular e \(Φ\) o potencial elétrico no horizonte.	A variação da energia interna do sistema relaciona-se com a variação da entropia, \(S\), do volume, \(V\), e do número de partículas, \(n\), por: \(\delta E=T\delta S-P\delta V+\mu\delta n\) onde \(P\) é a pressão e \(μ\) é o potencial químico.
Segunda Lei	Assumindo que a densidade de energia é positiva, então, a área do horizonte de eventos de um buraco negro nunca diminui: \(\delta A≥0\) Uma consequência é que da colisão de dois buracos negros, a área do horizonte de eventos do buraco negro resultante é maior que a soma das áreas dos buracos negros originais, o que é visualizado pelo chamado “diagrama de calças” em \(S^2\times\mathbb{R}\): 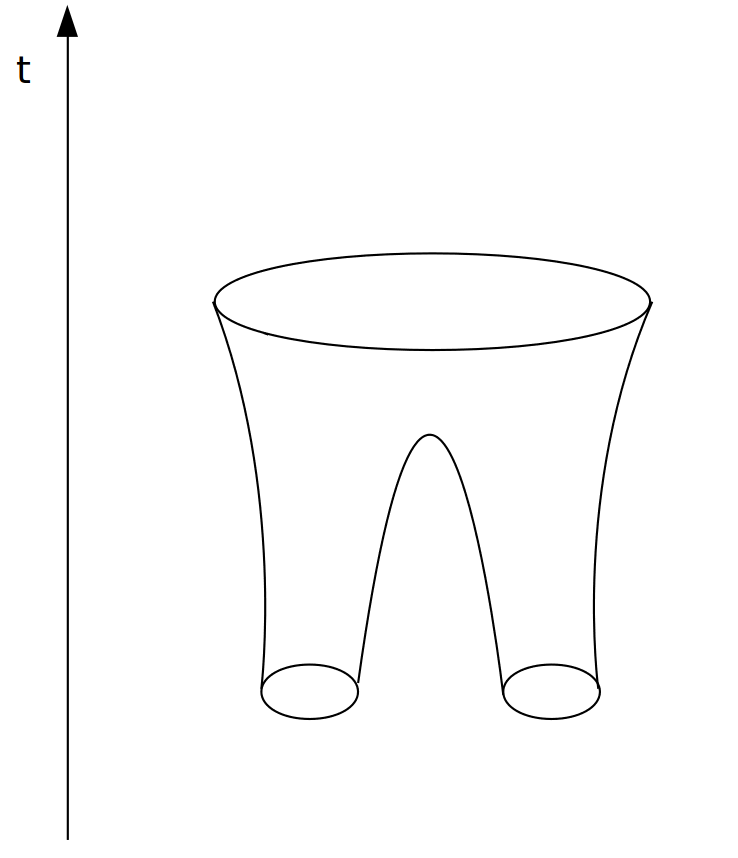Todavia, para ser compatível com a termodinâmica tem-se de considerar também a matéria circundante de um buraco negro.	A entropia de um sistema isolado nunca diminui: \(\delta S_{MAT}≥0\) Esta lei teve de ser generalizada para os buracos negros: a entropia total de um buraco negro e do seu exterior nunca diminui: \(\delta (S_{BN}+S_{MAT})≥0\), onde \(S_{BE}=\frac{c^3 A}{4Gℏ}\) é a entropia de Bekenstein-Hawking5,6.
Terceira Lei	Não são possíveis buracos negros com gravidade de superfície nula, excetuando os chamados buracos negros extremos, ou seja, quando se tem \(r_{sc}^2=\overline{Q}^2+a^2\) (ver acima).	A entropia de um sistema é uma constante bem definida e tende para zero à medida que a temperatura \(T\rightarrow 0K\). O zero absoluto \((T=0K)\) é inacessível, pois exige um número infinito de transformações termodinâmicas para ser atingido.

De facto, esta correspondência entre as leis geometro-dinâmicas dos buracos negros com as de uma termodinâmica adaptada a estes objetos é impressionante e sugere uma relação mais fundamental! Considerando a distribuição de Planck para um corpo negro com a temperatura de Hawking encontra-se a seguinte relação entre esta e a gravidade de superfície³: \(T_H=\frac{ℏκ}{2\pi k_B c}\). Assim, a entropia do buraco negro deverá corresponder a uma descrição macroscópica de um conjunto de microestados do sistema, no contexto de uma teoria quântica da gravidade, como, por exemplo, a teoria de cordas quânticas ou a gravidade quântica de “loop”⁷.