Iremos, aqui, apresentar uma descrição quantitativa do comportamento do fluido apenas nas vizinhanças do seu ponto crítico. Apesar desta restrição, ela é muito rica quer na obtenção de resultados analíticos quer na grande universalidade de tratamento dos mais variados fluidos e, mais geralmente, na unificação de descrições em muitos outros campos da Física onde ocorrem pontos críticos tais como em sistemas magnéticos ou ferroelétricos, supercondutores, cristais líquidos, etc. É, habitualmente, designada por teoria de Landau das transições de fase.

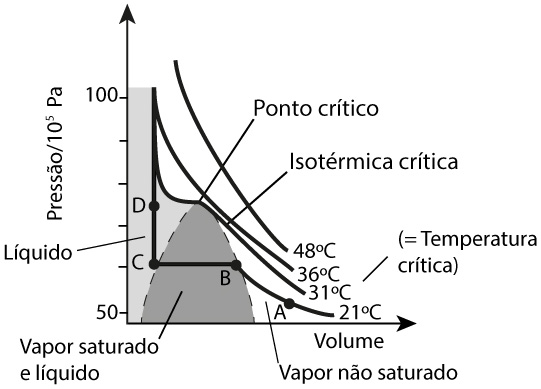
A Figura 1 mostra o diagrama de fases para o monóxido de carbono, mas que é típico para qualquer outro fluido (com uma só componente química). A isotérmica crítica apresenta um ponto de inflexão (ponto crítico) correspondente a uma pressão e volume bem definidos. Ela separa dois regimes: para temperaturas superiores, o fluido apresenta, apenas, uma fase; para temperaturas inferiores, existe uma região de equilíbrio das fases vapor e líquido (zona sombreada). O ponto crítico é, pois, definido, por serem nulas as primeira e segunda derivadas da pressão em ordem ao volume, i.e., tangente horizontal e mudança de curvatura, respetivamente:

\(\mathit{\left ( \frac{\partial p}{\partial V} \right )_{T_{c},V_{c}}=\left ( \frac{\partial ^{2}p}{\partial V^{2}} \right )_{T_{c},V_{c}}=0}\) (1)

Podemos, agora, aceitar, junto do ponto crítico, um desenvolvimento em série para a pressão, que o fluido exerce, em função do volume. Para isso, começamos por designar por \(\vartheta \equiv T-T_{c}\), o desvio da temperatura absoluta em relação à temperatura crítica; e por \(\vartheta \equiv \frac{V-V_{c}}{N}\), onde \(N\) é o número de partículas, o desvio do volume em relação ao volume crítico. Então, para \(\left | \vartheta \right |\ll T_{c}\) e \(\left | \vartheta \right |\ll \frac{V_{c}}{N}\), escrevemos:

\(p(v,\vartheta )=p_{c}-A\vartheta v+B\vartheta v^{2}-Cv^{3}+...\) (2)

\(C>0\) porque na isotérmic crítica \((\vartheta =0)\) a pressão diminui quando o volume aumenta;

\(A>0\) porque, para \(T>T_{c}\) (i.e.,\(\vartheta >0\)), a condição de estabilidade termodinâmica \(\left ( \frac{\partial p}{\partial p} \right )_{T}<0\) é verificada;

\(B>0\) porque, para \(T>T_{c}\) (i.e., \(\vartheta >0\)), a curvatura das isotérmicas é positiva \(\left ( \frac{\partial ^{2}p}{\partial v^{2}} \right )_{T}>0\).

(Note que, se utilizar a equação de van der Waals¹, obtém-se: \(A=\frac{6p_{c}}{T_{c},v_{c}};B=\frac{9p_{c}}{T_{c}v_{c}^{2}};C=\frac{3p_{c}}{2v_{c}^{3}}\).)

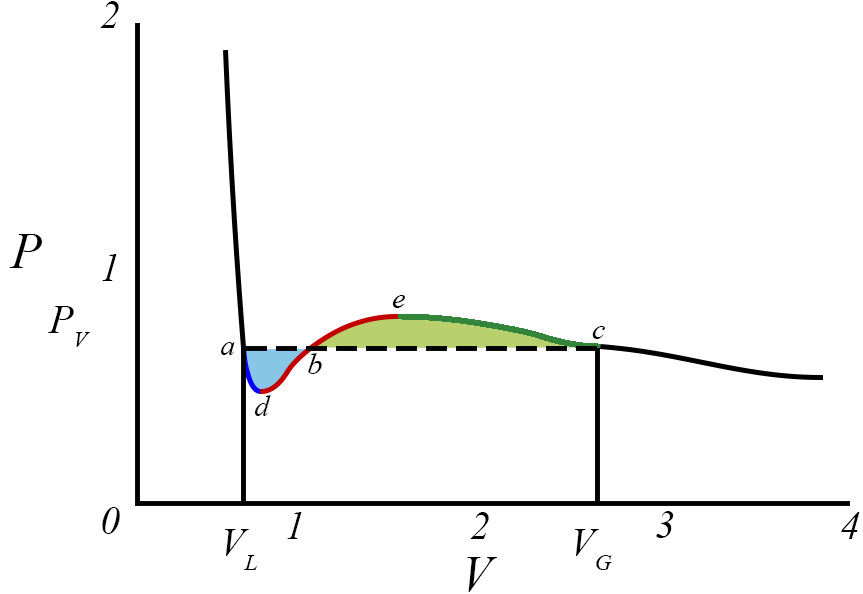
Contudo, abaixo de \(T_{c}\) a eq. (2) contém regiões de instabilidade termodinâmica que são regularizadas pela construção de Maxwell, como se mostra a seguir, e que é recordada na Figura 2. Para a isotérmica exibida, É determinada a pressão \(p\) de equilíbrio vapor-líquido exigindo a igualdade das áreas azul e amarela, isto é, pelo anulamento do trabalho ao longo do ciclo adbeca, isto é, \oint dv(p-p(v,\vartheta ))=0 porque, pela 2ª lei da Termodinâmica, não é possível extraír trabalho de um ciclo isotérmico. Assim:

\(p(v_{G}-v_{L})=\int_{v_{L}}^{v_{G}}dvp(v,\vartheta )\)

Adicionalmente, as coordenadas dos pontos \(a\) e \(c\) satisfazem à eq. (2) para a mesma pressão \(p\)

\(p=p(v_{G},\vartheta )=p(V_{L},\vartheta \)

Estas três equações determinam as três incógnitas \(p,v_{G}\) e \(v_{L}\). Efectuando estes cálculos, simples mas algo laboriosos, encontra-se:

\(v_{L}=-\sqrt{\frac{A\left | \vartheta \right |}{C}} v_{G}=\sqrt{\frac{A\left | \vartheta \right |}{C}} p=p_{c}-\frac{AB\vartheta ^{2}}{3C}\)

onde se conservaram, apenas, os termos de menor ordem em \(\vartheta \). Ficam, assim, encontrados os volumes das fases líquida e vapor, sendo este maior porque menor é a densidade do vapor, bem como a pressão de equilíbrio para a temperatura desta isotérmica. A Figura 2 mostra, também, que a fase liquida pode persistir até ao ponto \(d\) onde perde estabilidade porque \(\frac{\partial p}{\partial v}=0\) nesse ponto; analogamente, a fase de vapor pode persistir até ao ponto \(e\) onde perde estabilidade por ser nula a mesma derivada. Usando a eq. (2), é fácil encontrar as coordenadas destes pontos:

\(v_{d}=-\sqrt{\frac{A\left | \vartheta \right |}{3C}}\rightarrow p(d)=p_{c}-2C\left ( \frac{A\left | \vartheta \right |}{3C} \right )^{\frac{3}{2}}\)

\(v_{c}=-\sqrt{\frac{A\left | \vartheta \right |}{3C}}\rightarrow p(c)=p_{c}+2C\left ( \frac{A\left | \vartheta \right |}{3C} \right )^{\frac{3}{2}}\)

Quer isto dizer que, diminuindo a pressão, o fluido pode permanecer líquido até se atingir \(p(d)\), altura em que todo ele transita para vapor; do mesmo, aumentando a pressão, o fluido pode permanecer vapor até se atingir p(c), altura em que todo ele condensa em líquido.

Dois outros importantes resultados podem ser obtidos a partir da eq. (2):

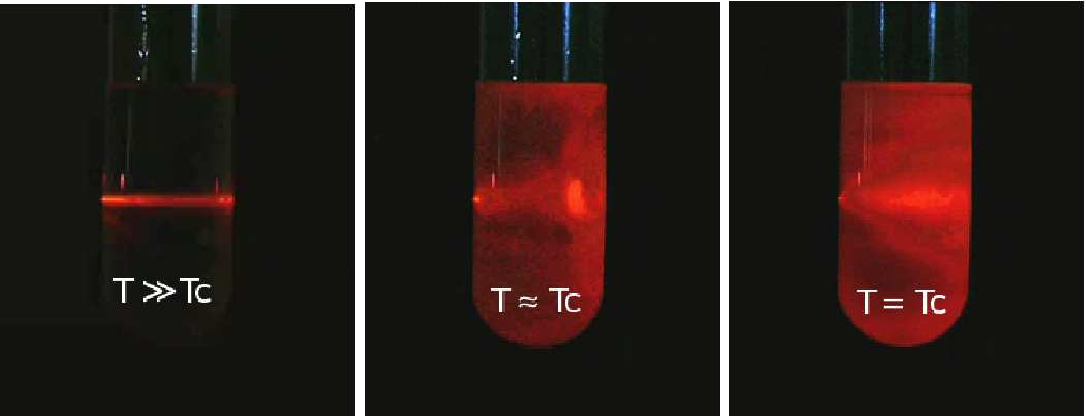
1º Acima da temperatura crítica \((\vartheta >0)\), se a pressão for ligeiramente aumentada de \(\delta p\), haverá uma ligeira diminuição de volume \(\delta v\cong -\frac{\delta p}{A\vartheta }\), pelo que a compressibilidade isotérmica \(k_{T}=\frac{1}{v}\left ( \frac{\partial v}{\partial p} \right )\cong \frac{1}{A\vartheta }\) diverge no ponto crítico. Tal significa que o mesmo número de partículas está a ocupar volumes sujeitos a grandes flutuações, i.e., há enormes flutuações na densidade, daí resultando flutuações divergentes do índice de refração: luz que seja enviada para o fluido nestas condições, sofre espalhamentos em todas as direções, um fenómeno conhecido por opalescência crítica (figura 3).

2º Mantendo o fluido na temperatura crítica \((\vartheta =0)\), a mesma eq. (2) mostra que, na vizinhança do ponto crítico, o volume já não varia linearmente com a pressão: \(v\cong \left ( \frac{p-p_{c}}{C} \right )^{\frac{1}{3}}\).

Estes expoentes que têm vindo a ser encontrados para diversas grandezas, junto do ponto crítico, são conhecidos por expoentes críticos e os seus valores aqui obtidos designam-se por expoentes críticos clássicos ou de campo médio. Eles voltam a ser encontrados em muitos outros tópicos da Física das Transições de Fase, sempre com os mesmos valores clássicos, mas que raramente são encontrados pelos resultados experimentais. Este desencontro entre os expoentes clássicos e os experimentais tem origem na não consideração das flutuações nas vizinhanças de pontos críticos, um tópico que não cabe aqui desenvolver.

A exposição anterior, baseada na construção de Maxwell, apresenta um problema de princípio. Com efeito, naquela construção, o ciclo isotérmico imaginado por Maxwell, contém, na sua parte “sinuosa” instabilidades termodinâmicas, i.e., regiões onde \(\left ( \frac{\partial p}{\partial v} \right )_{T}>0\). No que se segue, será apresentado um método diferente, assente na teoria de Landau, que evita a construção de Maxwell, mas que conduz aos mesmos resultados. Não podemos senão admirar a intuição de Maxwell: usando procedimentos pouco justificáveis, atingiu, contudo, resultados verdadeiros!

A teoria de Landau

O primeiro passo desta teoria é identificar a função termodinâmica que carateriza o equilíbrio termodinâmico. Essa função, deduzida, de forma simples, no apêndice, é:

\(\psi (v,\vartheta ,p_{0})=f(v,\vartheta )+p_{0}v\) (3)

onde \(f(v,\vartheta )\) é a energia livre de Helmholtz (dividida pelo número de partículas) e \(p_{0}\) é uma pressão constante, exteriormente aplicada sobre o sistema. O volume do sistema \(v\) não está determinado - é definido pela condição de equilíbrio termodinâmico do fluido: mínimo absoluto da função \(\psi \):

\(\left ( \frac{\partial \psi }{\partial v} \right )_{\vartheta ,p_{0}}=0\Leftrightarrow \left ( \frac{\partial f}{\partial v} \right )_{\vartheta }+p_{0}=0\Leftrightarrow p(v,\vartheta )=p_{0}\) (4)

Aqui, foi invocada a diferencial da energia livre²:

\(df(v,\vartheta )=-s(v,\vartheta )d\theta -p(v,\vartheta )dv\)

\(s(v,\vartheta )\) é a entropia (por partícula) e \(p(v,\vartheta )\)

é a pressão exercida pelo sistema que admitiremos ser definida pela eq. (2). Esta primeira condição de equilíbrio tem, assim, um significado simples: no equilíbrio, a pressão exercida pelo sistema é igual à pressão aplicada pelo exterior. Por outro lado, a condição determina o volume (ou volumes) do fluido no equilíbrio.

Mas só esta condição não basta: a função \(\psi \) deve apresentar um mínimo para as soluções encontradas pela primeira condição,isto é,

\(\left ( \frac{\partial ^{2}\psi }{\partial v^{2}} \right )_{\vartheta ,p_{0}}\geq 0\Leftrightarrow \left ( \frac{\partial ^{2}f}{\partial v^{2}} \right )_{\vartheta }\geq 0\Leftrightarrow -\left ( \frac{\partial p}{\partial v} \right )_{\vartheta }\geq 0\)

Vemos, aqui, a condição de estabilidade termodinâmica já antes recordada. Se houver mais do que um mínimo da função \(\psi \), o equilíbrio é determinado pelo mínimo absoluto: outros eventuais mínimos representam estados metastáveis. Se houver dois (ou mais) mínimos absolutos correspondentes ao mesmo valor de \(\psi \), teremos, então, equilíbrio de fases. O valor de \(\psi \) no mínimo é, então, \(f(v,\vartheta )+p(v,\vartheta )v\). É, afinal, o potencial químico do fluido e, portanto, o equilíbrio de fases é reinterpretável como igualdade dos potenciais químicos para cada fase.

Posto isto, comecemos por encontrar a função \(\psi (v,\vartheta ,p_{0})\) para a equação de estado definida em (2). Então, devemos, primeiro, encontrar a energia livre \(f(v,\vartheta )\) partindo de (2):

\(\left ( \frac{\partial f}{\partial v} \right )_{\vartheta }=-p(v,\vartheta )=-p_{c}+A\vartheta v-B\theta v^{2}+Cv^{3}+...\)

Integrando, obtém-se:

\(f(v,\vartheta )=f(0,\vartheta )-p_{c}v+\frac{1}{2}A\vartheta v^{2}-\frac{1}{3}B\vartheta v^{3}+\frac{1}{4}C\vartheta v^{4}+...\) (5)

As reticências representam termos de ordem superior em \(v\) . Serão ignoradas no que se segue.

Note-se que, aqui, \(f(0,\vartheta )\) é a energia livre para \(v=0\), isto é, \(V=V_{c}\). Agora, usando a eq. (3) tem-se:

\(\psi (v,\vartheta ,p_{0})=f(0,\vartheta )-(p_{c},\vartheta )-(p_{c}-p_{0})v+\frac{1}{2}A\vartheta v^{2}-\frac{1}{3}B\vartheta v^{3}+\frac{1}{4}Cv^{4}\)

O termo cúbico pode ser eliminado com uma simples mudança de variável:

\(v=\frac{B\vartheta }{3C}+\phi\) (6)

Substituindo e ignorando termos de ordem superior em \(\vartheta\), obtemos:

\(\psi (v,\vartheta ,p_{0})=f(0,\vartheta )-(p_{c}-p_{0})\frac{B\theta }{3C}+g(h,\phi ,\vartheta )\) (7)

onde:

\(g(h,\phi ,\vartheta )\equiv -h\phi +\frac{1}{2}A\vartheta \phi ^{2}+\frac{1}{4}C\phi ^{4}\) (8)

e:

\(h\equiv p_{c}-p_{0}-\frac{AB\vartheta ^{2}}{3C}\) (9)

Resumindo: a procura do mínimo de \(\psi \) em ordem a \(v\), equivale a procurar o mínimo de \(g(h,\phi ,\vartheta )\) em ordem a \(\phi \) : a eq. (6) relaciona estas duas variáveis. O parâmetro de controle exercido pela pressão exterior \(p_{0}\) é, na eq. (8), executado pelo “campo” \(h\).

A eq. (8) é a teoria de Landau das transições de fase de 2ª ordem. Como antes referido, ela aparece em tantos outros contextos da Física que vale a pena estuda-la, aqui, com algum detalhe.

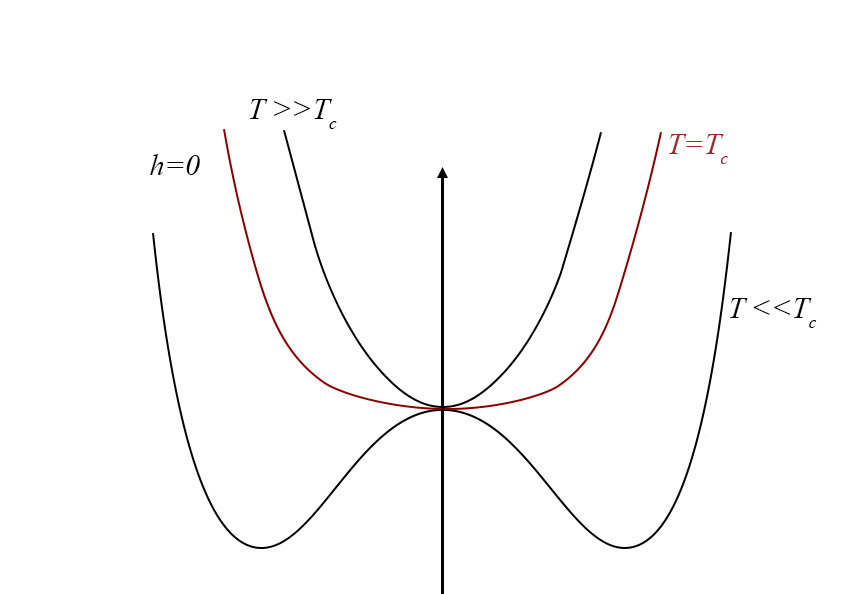
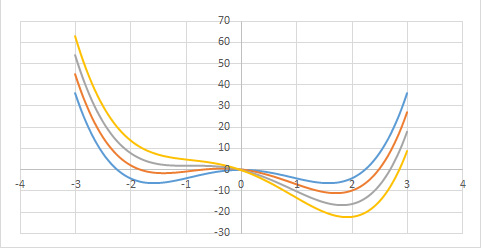
A Figura 4 exibe a função \(g(0,\phi ,\vartheta )\) para várias temperaturas.

1º Comecemos por considerar \(\vartheta >0\). A função \(g(h,\phi ,\vartheta )\) apresenta um único mínimo em \(\phi \) definido por \(A\vartheta \overline{\phi }\cong h\) (o termo quártico dá correções de ordem superior). Assim, para \(h\rightarrow 0\), obtém-se \(v\cong \overline{\phi }\cong \frac{P_{c}-p_{0}}{A\vartheta }\), resultado coincidente com o obtido atrás e que se traduz na divergência da compressibilidade isotérmica.

2º Na isotérmica crítica \((\vartheta =0)\), o termo quártico é dominante originando um mínimo na origem (para \(h=0\)) junto da qual a função \(g(\phi )\) permanece quase nula num domínio bastante alargado do seu argumento, o que se traduz por grandes flutuações no volume do fluido. Para \(h\neq 0\), o mínimo ocorre em \(\overline{\phi }\cong \left ( \frac{p_{c}-p_{0}}{C} \right )^{\frac{1}{3}}\), como já se encontrara.

3º Abaixo da temperatura crítica \((\vartheta <0)\), o termo quártico é fundamental para garantir a existência de mínimos. Observando a Figura 4, vemos que a função g(\phi ) apresenta dois mínimos, para \(h=0\), em ±\(\overline{\phi }\), com \(\overline{\phi }=\sqrt{\frac{A\left | \vartheta \right |}{C}}\) determinando o mesmo valor da função: trata-se, pois, de equilíbrio de duas fases: a líquida, de volume \(v_{L}=-\frac{B\left | \vartheta \right |}{3C}-\sqrt{\frac{A\left | \vartheta \right |}{C}}\), e vapor, de volume \(v_{V}=-\frac{B\left | \vartheta \right |}{3C}+\sqrt{\frac{A\left | \vartheta \right |}{C}}\), resultados já antes obtidos. As duas fases coexistem para \(h=0\), i.e., \(p_{c}-p_{0}=\frac{ABv^{2}}{3C}\), relação que define a curva de coexistência na Figura 1 (a tracejado). Mas, agora, podemos ir mais longe: usando a expressão da energia livre (eq. 5), deduzimos a entropia:

\(s(\vartheta ,v)=-\left ( \frac{\partial f}{\partial \vartheta } \right )_{\vartheta }=s(\vartheta ,0)-\frac{1}{2}Av^{2}+\frac{1}{3}Bv^{3}\)

Como são diferentes os volumes de líquido e vapor, há, então, uma diferença de entropia entre estas duas fases:

\(\Delta s\equiv s(\vartheta ,v_{V})-s(\vartheta ,v_{L})=\frac{4}{3}B\left ( \frac{A\left | \vartheta \right |}{C} \right )^{\frac{3}{2}}\)

Daqui decorre o calor latente de vaporização (dividido pelo número de partículas) \(l=T_{c}\Delta _{s}\propto \left | \vartheta \right |^{\frac{3}{2}}\), que se anula no ponto crítico, como sempre acontece em transições de 2ª ordem.

4º Se afastarmos a pressão externa \(p_{0}\) da linha de coexistência, o valor de h deixa de ser nulo, mas continuam a existir dois mínimos, um menor que o outro (Figura 5) enquanto não atingir um valor que se calculará a seguir. Considerando, como exemplo, que \(p_{0}\) diminui, \(h\) torna-se positivo: o mínimo absoluto ocorre para um valor \(\phi _{V}>0\), correspondendo à fase dominante de vapor, e o outro mínimo ocorre para \(\phi _{L}<0\), correspondente à fase líquida. Esta deve, então, ser considerada metastável porque o equilíbrio é definido pelo mínimo absoluto: a mínima perturbação poderá fazer o fluido saltar de \(\phi _{L}\) para \(\phi _{V}\) originando uma vaporização quase instantânea. Qual o valor de h que faz desaparecer o segundo mínimo? Para esse valor, a função \(g(\phi )\) apresentará, em \(\phi _{L}\) primeira e segunda derivadas nulas. Ora, \(g''(\phi )=-A\left | \vartheta \right |+3\phi ^{2}\), pelo que esse valor limite de \(\phi _{L}\) é \(\phi _{L}=-\sqrt{\frac{A\left | \vartheta \right |}{3C}}\). O anulamento da primeira derivada neste ponto fornece o valor de \(h\) procurado: \(h=-A\left | \vartheta \right |\phi _{L}+C\phi _{L}^{3}=2C\left ( \frac{A\left | \vartheta \right |}{3C} \right )^{\frac{3}{2}}\). Para valores superiores de \(h\), i.e., para \(p_{0}i.e., tornando \(h<0\), o mínimo absoluto situa-se na fase líquida e o mínimo relativo na fase de vapor, desaparecendo este para \(h<-2C\left ( \frac{A\left | \vartheta \right |}{3C} \right )^{\frac{3}{2}}\), i.e. \(p_{0}>p_{c}+2C\left ( \frac{A\left | \vartheta \right |}{3C} \right )^{\frac{3}{2}}\frac{AB\vartheta ^{2}}{3C}\).

Apêndice: Condição de equilíbrio para um sistema submetido a pressão exterior constante.

A 2ª lei da Termodinâmica informa que, num sistema isolado, onde são mantidos constantes a energia interna \(U\), o volume \(V\) e o número de partículas \(N\), a entropia evoluirá sempre para um máximo, o qual representa o estado de equilíbrio e onde a entropia é, apenas, função daquelas variáveis, \(S=S(U,V,N)\). Para um sistema em contacto com uma fonte de calor temperatura (absoluta) \(T\), o máximo da entropia para o conjunto sistema+fonte equivale ao mínimo da energia livre \(F=U-TS\) definida, apenas, para o sistema de interesse. Tal significa que qualquer processo espontâneo que ocorra no sistema, sempre em contacto com a fonte, a energia livre só pode diminuir, atingindo o mínimo no equilíbrio: a variação de \(F\) a partir deste mínimo não pode ser negativa. \(\delta F\geq 0\). Se o sistema está submetido a uma pressão constante \(p_{0}\), podendo variar o seu volume, o trabalho realizado por esta pressão para uma variação \(\delta V\) do volume, é \(-p_{0}\delta V\): a pressão externa realiza trabalho positivo se o volume diminuir \((\delta V<0)\). Ora, tal trabalho é igual à variação da energia livre, i.e., \(\delta F=-p_{0}\delta V\), ou \(\delta (F+p_{0}V)=0\). É, assim, a função \(\Psi =F+p_{0}V\) que deverá caraterizar o equilíbrio para volume variável do sistema submetido a pressão exterior constante e temperatura fixa.

Regressando à energia livre, a sua diferencial, no caso geral, é \(dF=-SdT-pdV+\mu dN\), onde \(p\) é a pressão exercida pelo sistema e \(\mu \) é o potencial químico o sistema. Assim, \(T\), \(V\) e \(N\) são os argumentos “naturais” da energia livre: \(F=F(T,V,N)\). Mas \(F\), tal como \(V\) e \(N\), é uma função extensiva, i.e., \(xF=F(T,xV,xN)\) para qualquer número real, positivo \(x\). Então, derivando em ordem a \(x\) e pondo \(x=1\), obtém-se:

\(F=V\frac{\partial F}{\partial V}+N\frac{\partial F}{\partial N}=-pV+\mu N\)

Quando se atinge o equilíbrio no sistema com volume variável, a função \(\Psi \) atinge um mínimo (em relação ao volume), caracterizado por \(p=p_{0}\). No mínimo, então, \(\Psi =F+pV=\mu N\). Assim, a função utilizada no texto \(\psi =\Psi /N\) é, no seu mínimo, \(\psi =\mu \), como foi referido.