A mecânica quântica nasceu em Dezembro de 1900 quando Max Planck deduziu a expressão matemática que obtivera, dois meses antes, como ajuste numérico, mas muito preciso, aos resultados experimentais relativos à intensidade da radiação emitida por um corpo negro. Na sua dedução, Planck postulou que um oscilador harmónico, de frequência natural \(v\), só pode ter as energias \(E_{n}=nhv\) com \(n=0,1,2,...\) e \(h=6,676...\times 10^{-34}Js\) uma constante que passou a ser conhecida por constante de Planck.

Em 1905, Albert Einstein analisou as flutuações de energia da radiação do corpo negro, concluindo que cada onda eletromagnética, de frequência \(v\), da radiação electromagnética transporta uma energia quantificada, como se fosse constituída por partículas com uma energia individual \(hv\), hipótese que viria a ser confirmada no efeito fotoelétrico. O quantum de luz passou, mais tarde, a designar-se por fotão.

Em 1913, Niels Bohr introduz o quantum no átomo de hidrogénio, postulando que as órbitas permitidas estão quantificadas nos estados estacionários, havendo emissão ou absorção de um fotão quando o eletrão salta de uma dessas órbitas para outra, obtendo desse modo as séries espectrais dos hidrogenóides (átomos ou iões com um único eletrão).

Em 1924, na sua tese de doutoramento, Victor de Broglie introduz a hipótese de cada partícula ter associada uma onda de comprimento:

\(\lambda =\frac{h}{p}\)(1)

onde \(p\) é o momento linear da partícula. Mostra que as órbitas permitidas de Bohr não são mais do que estados estacionários destas ondas.

Estes resultados, cada um dos quais merecedor de um artigo mais elaborado, estão, claramente, em contradição com a Física Clássica, mas revelaram-se de enorme valor na exploração inicial das propriedades atómicas e moleculares, fundamentando o que passou a ser conhecido por teoria quântica-clássica, um conjunto de regras enxertadas em modelos clássicos, justificando-se, apenas, pelo acordo com a experiência. Esta teoria ainda hoje é utilizada como primeira abordagem a um novo problema e constitui, realmente, a base da linguagem que usamos para descrever fenómenos à escala atómica.

Em Junho de 1925, Werner Heisenberg (FIGURA 1) inventa a mecânica matricial, um formalismo baseado unicamente em grandezas observáveis, representadas por matrizes, tendo ele mesmo deduzido o resultado de Planck e, no mesmo ano, Wolfgang Pauli obtém, usando aquela mecânica, a quantificação dos níveis de energia de Bohr. Em Outubro de 1925, Max Born e Pascual Jordan publicam a teoria completa da mecânica matricial, da qual deduzem um resultado bastante estranho:

\(\mathbf{xp}_{x}-\mathbf{p}_{x}\mathbf{x}=i\frac{h}{2\pi}\mathbf{1}\)(2)

Aqui, \(x\) e \(p_{x}\) são matrizes associadas, respetivamente, com a posição e o momento linear de uma partícula ( e \(1\) é a matriz unidade). Mas qual o significado físico desse resultado?

Em Janeiro de 1926, Erwin Schrödinger apresenta a mecânica ondulatória, baseada na hipótese de Victor de Broglie, e introduz a equação, que passou a ter o seu nome, para a função de onda \(\psi\) que descreve a partícula (ou, mais geralmente, o sistema), deduzindo quer a quantificação de Planck, quer os níveis de energia de Bohr e mostrando que o seu formalismo era equivalente ao de Heisenberg.

Mas qual o significado físico destes formalismos? Um primeiro passo foi obtido por Born: a função de onda \(\psi (x)\) contém toda a informação sobre a partícula, sendo que: \(\left | \psi (x) \right |^{2}dx\) é a probabilidade de uma medição da posição da partícula a encontrar em \(\left [ x,x+dx \right ]\).

Há, assim, um indeterminismo intrínseco na Mecânica Quântica, em completo contraste com o determinismo da Física Clássica. Com a interpretação de Born, podemos calcular onde, em média, se localiza a partícula:

\(\left \langle x \right \rangle=\int dx\left | \psi \left ( x \right ) \right |^{2}x\)

e, de modo análogo, se definem momentos de maior ordem. Em particular, o desvio padrão da posição:

\(\delta x=\sqrt{\left \langle x^{2} \right \rangle -\left \langle x \right \rangle^{2}}\)

Deste modo, podemos dizer que, com grande probabilidade, a partícula será encontrada em \(\left [ \left \langle x \right \rangle -\delta x,\left \langle x \right \rangle +\delta x\right ]\). Algumas observações importantes:

1ª O desvio padrão não tem qualquer relação com erros experimentais na medição da posição. Tais erros podem, em princípio, ser eliminados, reduzidos ou compensados. O desvio padrão, tal como a média, informa como se distribuem os resultados da medição das posições de um grande número de partículas idênticas, independentes e igualmente preparadas inicialmente, i.e., descritas pela mesma função de onda.

2ª Após a medição da posição da partícula, a função de onda não é mais a anterior \(\psi \left ( x \right )\) - diz-se que esta função de onda colapsou. A nova função de onda leva em conta o resultado obtido pela medição.

Podíamos, é claro, optar por medir o momento linear da partícula. Para tal, a sua distribuição de probabilidades é obtida a partir da transformada de Fourier de \(\psi \left ( x \right )\):

\(\phi \left ( p_{x} \right )=\frac{1}{\sqrt{h}}\int dxe^{i\frac{2\pi xp_{x}}{h}}\psi \left ( x \right )\)

Então, \(\left | \phi \left ( p_{x} \right ) \right |^{2}dp_{x}\) tem o mesmo significado anterior, agora adaptado a uma medição do momento linear, i.e., \(\left | \phi \left ( p_{x} \right ) \right |^{2}dp_{x}\) é a probabilidade de uma medição do momento linear da partícula a encontrar em \(\left [ px,px+dpx \right ]\). E, de modo análogo, definimos \(\left \langle p_{x} \right \rangle\) e \(\delta p_{x}\), respetivamente, o valor médio e o desvio padrão do momento linear, mantendo-se as observações atrás apresentadas:

\(\left \langle p_{x} \right \rangle=\int dp_{x}\left | \phi \left ( p_{x} \right ) \right |^{2}p_{x}\)

\(\delta p_{x}=\sqrt{\left \langle p_{x}^{2} \right \rangle-\left \langle p_{x} \right \rangle^{2}}\)

Ora, da eq. (2), deduz-se:

\(\delta x\delta p_{x}\geq \frac{h}{4\pi}\)(3)

Este resultado significa que medições infinitamente precisas e simultâneas da posição e do momento linear são impossíveis, em total contraste com a Física Clássica. Nada obsta a que, por exemplo, uma medição da posição tenha um erro \(\varepsilon _{x}\) mas, então, a determinação simultânea do momento linear terá uma imprecisão \(\varepsilon _{p_{x}}\geq \frac{h}{4\pi}\). É este o conteúdo do Princípio da Incerteza e a eq. (3) é a sua tradução matemática. Os pares de variáveis, tais como \(x\) e \(p_{x}\), satisfazendo à eq. (2) e, portanto, obedecendo ao Princípio da Incerteza, designam-se por variáveis conjugadas.

Os exemplos seguintes elucidam estas considerações.

Exemplo 1: Difracção por duas fendas

A FIGURA 2 esquematiza a experiência clássica de Young: luz monocromática (comprimento de onda \(\lambda\) incide sobre um anteparo vertical fixo onde existem duas fendas A e B, de largura \(a\ll \lambda\), distantes \(b\) uma da outra. A onda incidente é difractada pelas fendas, gerando uma figura de interferência no alvo, paralelo ao anteparo e a uma distância \(D\gg b\). A intensidade medida no alvo é:

\(I(\theta )=I_{0}\left [ cos\left ( \frac{\pi b}{\lambda} sen\left ( \theta \right )\right ) \right ]^{2}\)

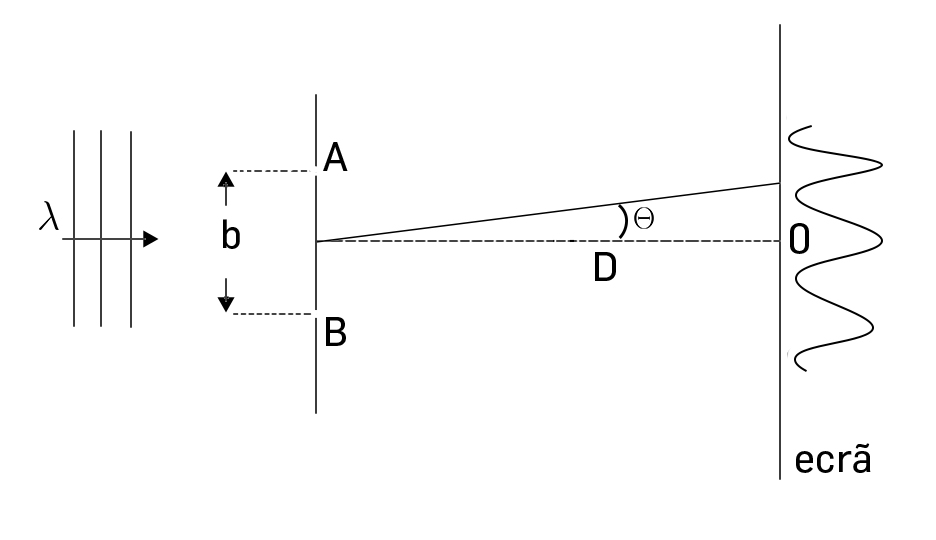
A figura de difracção, característica de um fenómeno ondulatório, é constituída por faixas iluminadas alternando com zonas escuras: as primeiras correspondem a máximos da intensidade \(\left ( sen\left ( \theta \right )=0,\pm \frac{\lambda}{b},\pm \frac{2\lambda}{b},... \right )\) e as segundas a intensidade nula. Aceitando, para simplificar, \(\lambda \ll b\ll D\), a distância, no alvo, entre máximos consecutivos (designada por interfranja) é \(\approx \frac{D}{b}\lambda =\frac{\lambda}{\alpha}\), onde \(\alpha\) é o ângulo, em O, do triângulo isóscele OAB.

Imaginemos, agora, que reduzimos a intensidade da onda incidente de modo a só existir um fotão em trânsito. Nestas circunstâncias, não se observa, no alvo, qualquer figura de interferência, antes um brilho aqui, outro além, aparentemente aleatórios, anunciando a detecção dos correspondentes fotões (FIGURA 3). Para cada fotão, não sabemos a que ponto do alvo chegará; mas se registarmos as posições de chegada de sucessivos fotões, vemos emergir a figura de interferência. Quer dizer, a figura de interferência representa a estatística de chegada ao alvo dos fotões!

Há uma outra questão interessante: por qual das fendas passou um fotão? Com a montagem experimental acima indicada, não é possível responder à questão. Mas podemos alterar essa montagem, por exemplo, suspendendo o anteparo, com as duas fendas, por uma mola. Considere-se um fotão detectado em \(\theta =0\): se passou pela fenda A, adquiriu um momento linear \(-\frac{p\alpha}{2}\) segundo o eixo vertical (eixo \(y\)), obrigando o anteparo a “subir” (\(p=\frac{h}{\lambda}\) é o momento linear do fotão); se passar pela fenda B, adquire o momento \(\frac{p\alpha}{2}\), obrigando o anteparo a “descer” (FIGURA 4).

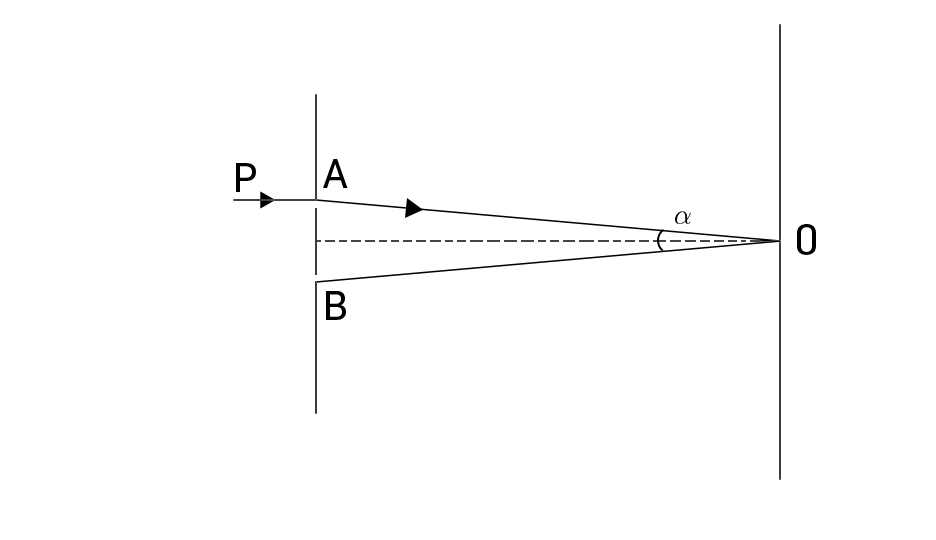
Observando o movimento do anteparo, saberíamos por qual das fendas passou o fotão. Mas, para isso, necessitamos de conhecer o momento linear do anteparo com uma precisão \(\delta P_{y}\ll \frac{p\alpha}{2}\); então, pela relação de Heisenberg, a posição do anteparo tem uma incerteza \(\delta y\approx \frac{h}{2\delta P_{y}}\gg \frac{h}{p\alpha }=\frac{\lambda}{2\pi \alpha }\), i.e., muito maior que a interfranja. Quer dizer, a identificação da fenda por onde passou o fotão destrói a figura de interferência!

De modo inverso, se queremos manter a figura de interferência, o momento linear da parede deve ser nulo com uma imprecisão \(\delta P_{y}\ll p\theta \), onde \(\theta\) é a separação angular entre um máximo e um mínimo consecutivos da figura de interferência: \(\theta =\frac{\lambda}{2b}\). Assim, \(\delta P_{y}\ll \frac{p\lambda}{2b}=\frac{h}{2b}\), pelo que (relação de Heisenberg) a imprecisão na posição do anteparo é \(\delta y\approx \frac{h}{2\delta P_{y}}\gg \frac{b}{2\pi}\), i.e., não sabemos por qual das fendas passou o fotão!

Há muitas outras experiências conceptuais semelhantes à aqui considerada (ver Referências) - em todas elas, o resultado é o anterior: se soubermos por qual fenda passou o fotão (natureza corpuscular), destruímos a figura de interferência (natureza ondulatória), e vice-versa. As duas naturezas excluem-se mutuamente, mas são complementares, no sentido em que cada uma ilumina um aspecto do comportamento observado. Outras importantes conclusões estão remetidas para os comentários finais.

Exemplo 2: O microscópio de Heisenberg

Imaginemos um microscópio com a objectiva focada sobre uma linha onde se situa um electrão praticamente em repouso (FIGURA 5). Um fotão (raio \(\gamma\),) de momento \(p=\frac{h}{\lambda}\), colide com o eletrão sob o foco da lente e é desviado (efeito Compton) para a objectiva, sendo detetado pelo observador. Designando por \(\theta\) a abertura angular da lente (objectiva), parece que podemos conhecer exactamente quer a posição do electrão quer o seu momento linear após colisão \(p_{x}=psen\left ( \frac{\theta }{2} \right )\). Mas não é assim! Com efeito, o fotão foi desviado para o interior do cone de focagem, não se sabendo exactamente a sua trajectória, pelo que há a imprecisão \(\delta p_{x}=psen\left ( \frac{\theta }{2} \right )\) no momento linear.

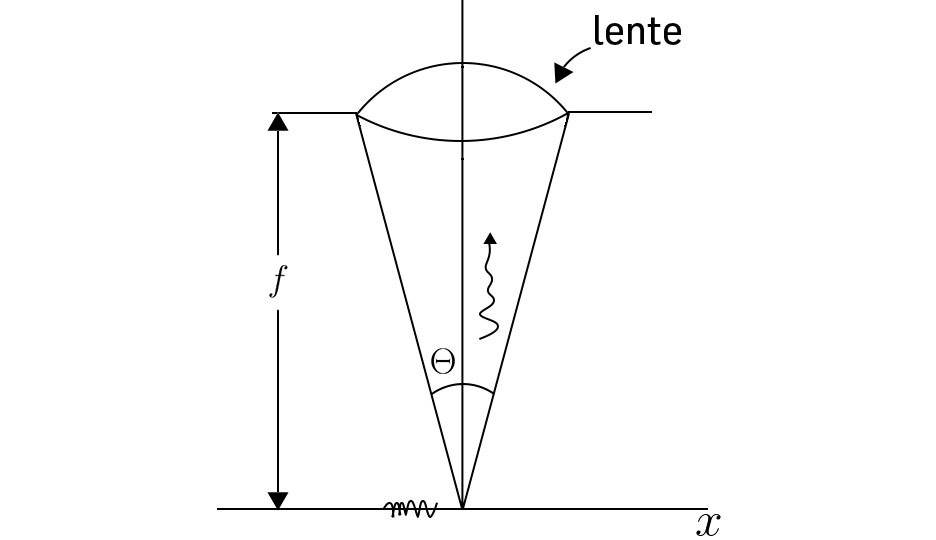
Por outro lado, a onda electromagnética de que o fotão é o quantum, com um comprimento de onda \(\lambda\), difracta nos bordos da lente, o que limita o poder separador do microscópio: se o electrão se situar sob o foco com uma imprecisão de posição \(\delta x\approx \frac{\lambda}{2sen\frac{\theta }{2}}\), sua imagem é a mesma. Assim:

\(\delta x\delta p_{x}\approx \frac{p\lambda}{2}=\frac{h}{4\pi}\)

tal como exigido pela relação de incerteza.

Exemplo 3: Desvio num campo magnético

Uma partícula (massa \(m\), carga \(q\), momento linear \(p\)) incide perpendicularmente sobre uma abertura (largura \(a\)) para além da qual existe um campo magnético uniforme \(B\).

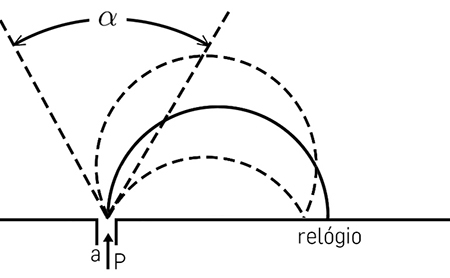
O campo desvia a partícula fazendo-a incidir sobre um detetor, na parede, que regista o “tempo de voo”, da entrada ao detetor (FIGURA 4). Em Física Clássica, este dispositivo poderia servir para determinar a energia da partícula. Com efeito, ela descreve uma semicircunferência (raio R é metade da distância da abertura ao detector) com a velocidade angular \(\omega _{c}=\frac{qB}{m}\) (frequência ciclotrónica). Assim, a velocidade da partícula é \(\nu =\omega _{c}R\), conhecendo-se quer a sua energia, \(E=\frac{1}{2}m\nu ^{2}\), quer o tempo do voo, \(t=\frac{\pi}{\omega _{c}}\). Contudo, a análise é um pouco mais elaborada. Comecemos por notar que o raio tem uma imprecisão \(\delta R\approx \frac{a}{2}\), devido à largura finita da abertura. Por outro lado, a partícula tem uma onda associada (de Broglie), de comprimento \(\lambda=\frac{h}{p}\). A onda vai, necessariamente, difractar na abertura, originando uma imprecisão \(\delta \alpha \approx \frac{\lambda}{a}\) no angulo que define a direcção inicial da velocidade dentro do campo. Como consequência, a trajectória é um arco de círculo que se inicia subtendendo um ângulo no intervalo \(\left [ \pi -\frac{\delta \alpha}{2},\pi +\frac{\delta \alpha}{2} \right ]\), pelo que o tempo de voo tem uma incerteza \(\delta t\approx \frac{\delta \alpha}{2\omega _{c}}\). Ora, a imprecisão no raio determina uma imprecisão na velocidade: \(\delta E=m\nu \delta \nu =\frac{p\omega _{c}a}{2}\). Assim:

\(\delta E\delta t\approx \frac{p\lambda}{4}=\frac{h}{4}\)(4)

Esta é uma outra forma do Princípio da Incerteza, relacionando, genericamente, a imprecisão na energia de um sistema com a imprecisão no tempo durante o qual o sistema interagiu com outro para medir essa mesma energia . Uma importante aplicação deste resultado é a seguinte: um átomo ou molécula num estado excitado decai, ao fim de algum tempo, para o estado fundamental; este tempo de decaímento não é conhecido (obedece, frequentemente, a uma distribuição de Poisson), mas tem um valor médio \(\tau\). Há, assim, uma imprecisão \(\delta E\approx \frac{h}{\tau }\) na energia do estado excitado, originando uma imprecisão \(\delta \omega \approx \frac{1}{\tau }\) na frequência da luz emitida: esta imprecisão é conhecida por largura intrínseca da risca.

Comentários finais

Não terá passado despercebido ao leitor que, no primeiro exemplo atrás considerado, a relação de incerteza foi aplicada ao anteparo com as duas fendas, um objecto macroscópico. Não há uma linha divisória que separe um domínio onde se aplica a teoria quântica de outro onde impera a Física Clássica. A teoria quântica não prescinde da Física Clássica porque aceita ser nesta que, para efeitos práticos, funcionam os aparelhos de medida, se registam leituras exatas (a menos de erros experimentais) e fundamenta a linguagem que descreve os fenómenos limitada, como está, pela nossa experiência “macroscópica”. Mas um aparelho de medida (tal como o anteparo) pode ele próprio revelar-se um sistema quântico, sujeito ao Princípio da Incerteza, se, para tal, forem reunidas as condições necessárias. Para observar esse comportamento quântico, temos de empregar outros aparelhos que, para efeitos práticos, obedecem à Física Clássica. O anteparo, por exemplo, está sujeito a flutuações térmicas: para uma massa de 0,1Kg, o seu momento linear médio, devido à agitação térmica, é \(p\approx 2\times 10^{-11}\) Kgm/s, e se o erro experimental na medida da sua posição for 10-³m, então ter-se-á \(\delta p\delta x\approx 2\times 10^{-14}Js\), muito maior que a constante de Planck. Estes erros experimentais não impedem o anteparo de originar a figura de interferência; mas se quisermos, como naquele primeiro exemplo, que o anteparo se comporte como um objecto quântico, temos de anular todas as fontes de ruído (flutuações térmicas ou da pressão, dilatações por absorção de luz, etc.). É evidente que isso é experimentalmente muito difícil de conseguir para objectos macroscópicos e é por isso que o comportamento quântico é, sobretudo, observado em sistemas de pequena dimensão, tais como átomos ou moléculas.

Por último, o leitor questionará: o fotão ou o electrão são, afinal, partículas ou ondas? A resposta, seguindo Bohr, é a seguinte: a Física não se debruça sobre o que é, mas sim sobre como se comporta. E o mesmo Bohr dá uma definição de fenómeno que passou a ser aceite por toda a comunidade física: um fenómeno é uma observação, incluindo os meios usados para observar. Assim, as palavras “fotão” ou “electrão” designam fenómenos que se comportam como partículas quando usamos métodos para detectar partículas e se comportam como “ondas” quando usamos métodos para detectar ondas. Os dois comportamentos nunca são observados em simultâneo e ambos informam sobre tais fenómenos, auto-excluindo-se, mas complementando-se. Tal é o conteúdo do Princípio da Complementaridade (Bohr, 1927).

Feynman¹ apresenta uma excelente discussão sobre a experiência de difração por duas fendas com deteção individual de fotões. A dedução formal das relações de incerteza pode ser encontrada no bem conhecido texto de Schiff². Para os fundamentos e aplicações da teoria quântica, o teto de Park³ é bastante completo e fácil de ler.