O Sistema Internacional de Unidades (SI)
📧
- UNSW Sydney/ IUPAC/ CICECO/ Universidade de Aveiro
Referência Magalhães, C., (2021) O Sistema Internacional de Unidades (SI), Rev. Ciência Elem., V9(1):003
DOI http://doi.org/10.24927/rce2021.003
Palavras-chave Sistema Internacional de Unidades; SI; unidade de base; unidade fundamental; massa; kilograma; quilograma; tempo; segundo; comprimento; metro; corrente elétrica; ampere; temperatura termodinâmica; kelvin; intensidade luminosa; candela
Resumo
As definições das unidades do Sistema Internacional de Unidades (SI) assentam em sete unidades de base para as quais há novas definições para a unidade de base da massa, o kilograma, e a unidade de base da quantidade de matéria, a mole, que passaram a vigorar internacionalmente a partir de 20 de maio de 20191. A tradução portuguesa oficial foi fixada pelo Decreto-Lei nº 76/2020 de 25 de setembro2.
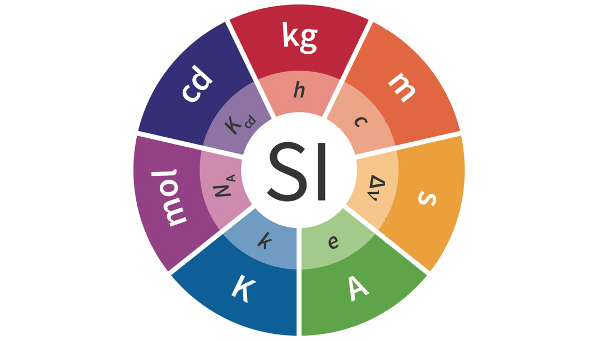
As novas definições das unidades de base (unidades fundamentais), pretendem criar um sistema coerente que assenta nos valores exatos de sete constantes universais que são, por definição, invariáveis e imutáveis. Os valores exatos das constantes universais fixados em acordo com os valores, anteriormente, determinados experimentalmente em diversos laboratórios internacionais de metrologia através das melhores técnicas disponíveis, foram definidos pelo Comité de Dados para a Ciência e Tecnologia (CODATA) e adotados pela 26ª reunião da Conferência Geral de Pesos e Medidas (CGPM), que se reuniu em Versailles de 13 a 16 de novembro de 20181, 2.
Na TABELA 1 apresentam-se as sete constantes universais, os respetivos símbolos, os valores fixados como exatos, pelo que não têm qualquer incerteza associada, e a respetiva unidade2.
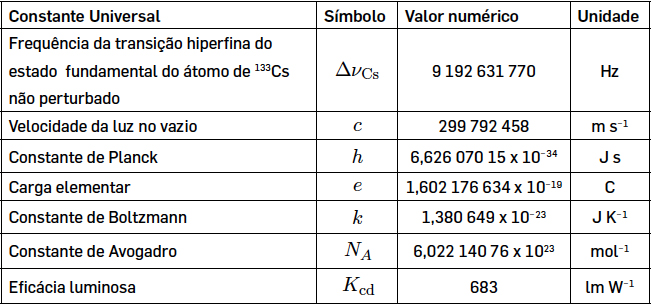
Estas constantes universais foram escolhidas de modo a que cada unidade de base possa ser definida a partir dessas constantes ou a partir de produtos ou quocientes dessas constantes. Entre as unidades hertz (Hz), joule (J), coulomb (C), lúmen (lm) e watt (W) e as unidades segundo (s), metro (m), kilograma (kg), ampere (A), kelvin (K), mole (mol) e candela (cd) existem as relações seguintes:
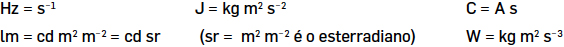
Na TABELA 2 apresentam-se as sete grandezas fundamentais, respetivas unidades de base, símbolos das unidades e as constantes universais a partir das quais se define diretamente a respetiva unidade de base.1, 2

Definições das unidades fundamentais
Todas as definições estão redigidas com um formato semelhante – primeiro indica-se para cada grandeza física qual a unidade de base e respetivo símbolo. Numa outra frase define- se a relação entre a unidade de base e a constante universal com a qual se relaciona e como se relaciona. Como se pode ver pelo texto há uma certa ordenação na definição das unidades das várias grandezas, uma vez que algumas delas necessitam de mais do que uma constante universal para a sua definição.
Unidade de tempo
O segundo, símbolo s, é a unidade de tempo do SI. Define-se tomando o valor numérico fixado da frequência do césio, \(\Delta\nu_{\textrm{Cs}}\), a frequência da transição hiperfina do estado fundamental do átomo de césio-133 não perturbado, igual a 9 192 631 770, quando expressa na unidade hertz, que é igual a s-1.
Esta definição implica a relação exata:
\(\Delta\nu_{\textrm{Cs}}\)= 9 192 631 770 Hz ou \(\Delta\nu_{\textrm{Cs}}\)= 9 192 631 770 s−1
\(\textrm{1 s}=\frac{9\; 192\; 631\; 770}{\Delta\nu_{\mathrm{Cs}}}\)
Um segundo é o tempo que demoram 9 192 631 770 períodos da radiação resultante da transição entre dois níveis hiperfinos do estado fundamental do átomo 133Cs não perturbado.3
Unidade de comprimento
O metro, símbolo m, é a unidade de comprimento do SI. Define-se tomando o valor numérico fixado da velocidade da luz no vazio, \(c\), igual a 299 792 458, quando expressa na unidade m s-1, sendo o segundo definido em função de \(\Delta\nu_{\textrm{Cs}}\).
Esta definição implica a relação exata:
\(c\)= 299 792 458 m s−1
\(\textrm{1 m}=\left ( \frac{c}{299\; 792\; 458} \right )\textrm{s}=\frac{9\; 192\; 631\; 770}{299\; 792\; 458}\frac{c}{\Delta\nu_{\mathrm{Cs}}}=30,663\; 319\; 0\frac{c}{\Delta\nu_{\mathrm{Cs}}}\)
Um metro é o comprimento percorrido pela luz no vazio no intervalo de tempo de 1 / 299 792 458 do segundo.3
Unidade de massa
O kilograma, símbolo kg, é a unidade de massa do SI. Define-se tomando o valor numérico fixado da constante de Planck, \(h\), igual a 6,626 070 15 x 10−34, quando expressa na unidade J s, que é igual a kg m2 s-1, sendo o metro e o segundo definidos, respetivamente, em função de \(c\) e \(\Delta\nu_{\textrm{Cs}}\).
Esta definição implica a relação exata:
\(h\) = 6,626 070 x 10−34 kg m2 s−1
\(\textrm{1 kg}=\left ( \frac{h}{6,626\; 070\; 15\times^{-34}} \right )m^{-2}s\)
\(\textrm{1 kg}=\frac{\left ( 299\; 792\; 458 \right )^{2}\left ( 9\; 192\; 631\; 770 \right )}{\left ( 9\; 192\; 631\; 770 \right )^{2}\left ( 6,626\; 070\; 15\times10^{-34} \right )}\frac{\left ( \Delta\nu_{\mathrm{Cs}} \right )^{2}h}{\Delta\nu_{\mathrm{Cs}}\; c^{2}}=\)
\(=\frac{\left ( 299\; 792\; 458 \right )^{2}}{\left ( 9\; 192\; 631\; 770 \right )\left ( 6,626\; 070\; 15\times 10^{-34} \right )}\frac{\left ( \Delta\nu_{\mathrm{Cs}} \right )h}{c^{2}}\)
\(\textrm{1 kg}=1,475\; 521\; 40\times10^{40}\frac{\left ( \Delta\nu_{\mathrm{Cs}} \right )h}{c^{2}}\)
A definição de kilograma só é possível em função da constante de Planck.3
Unidade de corrente elétrica
O ampere, símbolo A, é a unidade de corrente elétrica do SI. Define-se tomando o valor numérico fixado da carga elementar, \(e\), igual a 1,602 176 634 x 10−19, quando expressa na unidade C, que é igual a A s, sendo o segundo definido em função de \(\Delta\nu_{\textrm{Cs}}\).
Esta definição implica a relação exata:
\(e\) = 1,602 176 634 x 10−19 A s
\(\textrm{1 A}=\left ( \frac{e}{1,602\; 176\; 634\times10^{-19}} \right )\; \textrm{s}^{-1}\)
\(\textrm{1 A}=\frac{1}{\left ( 1,602\; 176\; 634\times 10^{-19} \right )\left ( 9\; 192\; 631\; 770 \right )}\Delta\nu_{\mathrm{Cs}}e=\)
\(=6,789\; 686\; 817\times^{8}10^{8}\Delta \nu_{\mathrm{Cs}}\; e\)
Um ampere é a corrente elétrica correspondente ao fluxo de 1 / (1,602 176 634 x 10−19) cargas elementares por segundo.3
Unidade de temperatura termodinâmica
O kelvin, símbolo K, é a unidade de temperatura termodinâmica do SI. Define-se tomando o valor numérico fixado da constante de Boltzmann, \(k\), igual a 1,380 649 x 10−23, quando expressa na unidade J K-1}, que é igual a kg m2 s-2 K-1, sendo o kilograma, o metro e o segundo definidos, respetivamente, em função de \(h\), \(c\) e \(\Delta\nu_{\textrm{Cs}}\).
Esta definição implica a relação exata:
\(k\) = 1,380 649 x 10−23 kg m2 s−2 K−1
\(\textrm{1 K}=\left ( \frac{1,380\; 649}{k} \right )\times 10^{-23}\textrm{kg}\; \textrm{m}^{2}\; \textrm{s}^{-2}\)
\(\textrm{1 K}=\frac{1,380\; 649\times 10^{-23}}{\left ( 6,626\; 070\; 15\times 10^{-34} \right )\left ( 9\; 192\; 631\; 770 \right )}\frac{\Delta\nu_{\mathrm{Cs}}h}{k}=\)
\(=2,266\; 665\frac{\Delta\nu_{\mathrm{Cs}}h}{k}\)
Um kelvin é igual à variação da temperatura termodinâmica que resulta da variação de 1,380 649 x 10−23 J na energia térmica \(kT\).3
Unidade de intensidade luminosa
A candela, símbolo cd, é a unidade de intensidade luminosa do SI numa dada direção. Define-se tomando o valor numérico fixado da eficácia luminosa de uma radiação monocromática de frequência 540 x 1012 Hz, \(K\)cd, igual a 683, quando expressa na unidade lm W-1, que é igual a cd sr W-1 ou cd sr kg-1 m-2 s3, sendo o kilograma, o metro e o segundo definidos, respetivamente, em função de \(h\), \(c\) e \(\Delta\nu_{\textrm{Cs}}\).
Esta definição implica a relação exata:
\(K\)dc= 683 cd sr kg−1 m−2 s3
para a radiação monocromática com a frequência 540 x 1012 Hz.
\(\textrm{1 cd}=\left ( \frac{K_{\mathrm{cd}}}{683} \right )\textrm{kg}\; \textrm{m}^{2}\; \textrm{s}^{-3}\; \textrm{sr}^{-1}\)
\(\textrm{1 cd}=\frac{1}{\left ( 6,626\; \; 070\; 15\times 10^{-34} \right )\left ( 9\; 192\; 631\; 770 \right )^{2}683}\left ( \Delta\nu_{\textrm{Cs}} \right )^{2}h\; K_{\textrm{cd}}=\)
\(=2,614\; 830\times 10^{10}\left ( \Delta\nu_{\textrm{Cs}} \right )^{2}h\; K_{\textrm{cd}}\)
Uma candela é a intensidade luminosa, numa dada direção, de uma fonte que emite uma radiação monocromática de frequência 540 × 1012 Hz e cuja intensidade energética nessa direção é 1/683 W/sr.3
Unidade de quantidade de matéria
A mole, símbolo mol, é a unidade de quantidade de matéria do SI. Uma mole contém exatamente 6,022 140 76 x 1023 entidades elementares. Este número é o valor numérico fixado da constante de Avogadro, \(N\)A, quando expressa em mol-1 e é designado por “número de Avogadro”.
A quantidade de matéria, símbolo \(n\), de um sistema é uma representação do número de entidades elementares especificadas. Uma entidade elementar pode ser um átomo, uma molécula, um ião, um eletrão, ou qualquer outra partícula ou agrupamento especificado de partículas.
Esta definição implica a relação exata:
\(N\)A = 6,022 140 76 x 1023 mol−1
\(\textrm{1 mol}=\frac{6,022\; 140\; 76\times 10^{23}}{N_{\textrm{A}}}\)
Uma mole é a quantidade de matéria de um sistema que contém 6,022 140 76 x 1023 das entidades elementares especificadas.3
NOTA
O Decreto-Lei nº 76/2020 de 25 de setembro utiliza as denominações quantidade de matéria para quantidade de substância e eficácia luminosa para eficiência luminosa.
Referências
- 1 BUREAU INTERNATIONAL DES POIDS ET MESURES (BIPM), Le Système international d’unités/The International System of Units, BIPM, Sèvres, France, 9, 216 p. 2019. (consultado em 12 de fevereiro de 2021)
- 2 DIÁRIO DA REPÚBLICA, Decreto-Lei nº 76/2020, 1ª Série, nº 188, 12-21.
- 3 BUREAU INTERNATIONAL DES POIDS ET MESURES (BIPM), Les unités de mesure: Le SI. (consultado em 12 de fevereiro de 2021)
Este artigo já foi visualizado 19225 vezes.



