Forças em campos magnéticos
📧
- Universidade do Porto
Referência Lage, E., (2021) Forças em campos magnéticos, Rev. Ciência Elem., V9(1):017
DOI http://doi.org/10.24927/rce2021.017
Palavras-chave campos magnéticos, LHC, aceleradores, ciclotrão, correntes, espiras, força de Laplace, força electromotriz, indução de Faraday
Resumo
O movimento de partículas carregadas em campos magnéticos estacionários é de grande importância em Física e Astrofísica estando na base dos grandes aceleradores, como LHC no CERN, de que o ciclotrão foi precursor. E também determinam a natureza dos transportadores no efeito Hall. As forças entre correntes elétricas, mensuráveis em diversos tipos de dispositivos, foram historicamente utilizadas na definição do ampére, a unidade da intensidade da corrente no SI. Para correntes localizadas e submetidas a um campo magnético quase uniforme, a força que este exerce deriva de uma energia potencial que faz intervir apenas o momento magnético daquele sistema de correntes.
É apresentada uma breve discussão sobre a relação entre os trabalhos, em espiras, da força de Laplace e da força eletromotriz originada pela indução de Faraday, mostrando- se que ambos derivam de ser nula a potência da força de Lorentz.
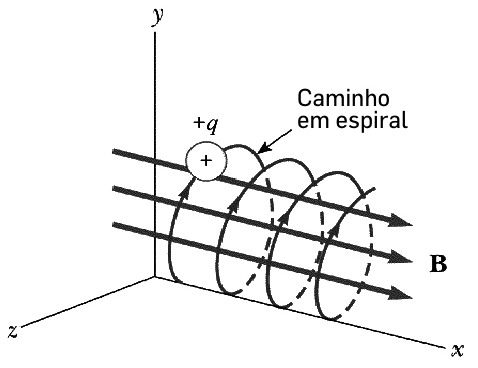
Partículas com carga elétrica (eletrões, protões, iões, etc.) em movimento numa região onde existe um campo magnético, ficam submetidas à força de Lorentz1, apresentando uma rica variedade de comportamentos com inúmeras aplicações. A FIGURA 1 representa um exemplo simples para um campo uniforme: projetando nos eixos a equação de movimento, tem-se:
\(\frac{dv_{x}}{dt}=0\rightarrow v_{x}=\textrm{constante}\)
\(\frac{dv_{y}}{dt}=\omega _{c}v_{z}\) (1)
\(\frac{dv_{z}}{dt}=\omega _{c}v_{y}\)
onde:
\(\omega _{c}=\frac{qB}{m}\) (2)
é a frequência ciclotrónica (\(q\) e \(m\) são a carga e massa da partícula). Se \(v_{x}=0\), o movimento é uniforme e circular com um raio:
\(R=\frac{1}{\omega _{c}}\sqrt{v_{y}^{2}+v_{z}^{2}}\) (3)
Um ciclotrão (E. Lawrence, 1932) é constituído por dois semicilindros (os “Dês”) onde se fez o vácuo, mergulhados num campo magnético uniforme com a direção do eixo dos cilindros.
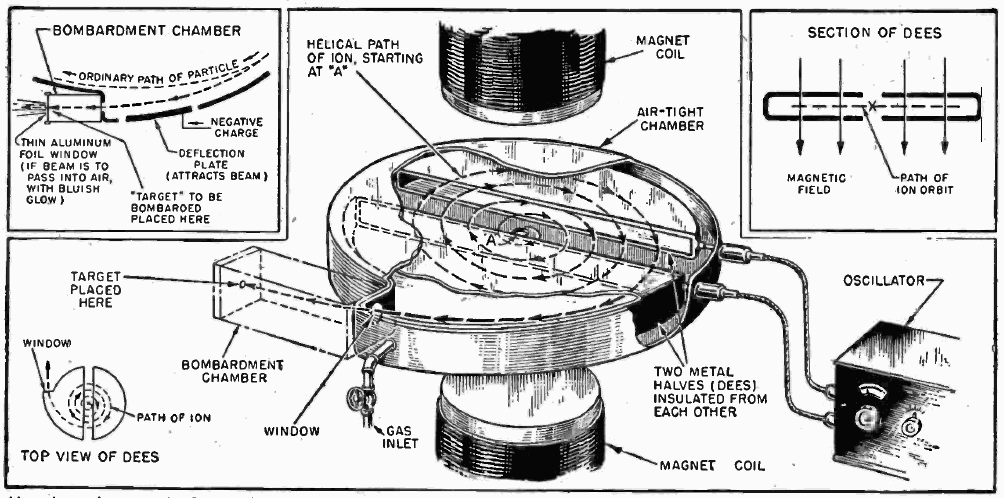
Entre as faces planas dos “Dês” é aplicada uma tensão de radiofrequência que origina um campo elétrico capaz de acelerar as partículas antes de penetrarem no campo magnético. O correspondente movimento circular fá-las regressar à região do campo RF, tendo este a frequência ciclotrónica pelo que, em cada volta da partícula num “Dê”, se encontra nas condições para nova aceleração. Deste modo, a partícula vai ganhando energia, aumentando o raio da trajetória circular. O aumento relativista da massa da partícula origina uma diminuição da frequência ciclotrónica – o campo RF sincroniza a sua frequência com aquela, designandose por sincrociclotrão um tal acelerador.
Regressando à FIGURA 1, é este movimento helicoidal que desvia raios cósmicos ou o vento solar para os polos magnéticos da Terra onde colidem e ionizam moléculas da alta atmosfera originando as auroras boreais. Uma carga acelerada emite radiação: num pulsar, uma estrela de neutrões em rápida rotação cujo eixo não coincide com o dipolo magnético2, o fortíssimo campo magnético origina emissões de grande intensidade na direção NS magnética a qual roda com a estrela, como se fosse um farol. Esta radiação é recebida na Terra, caso esta se encontre no alinhamento da emissão: a extrema regularidade destes impulsos de radiação, com períodos de rotação característicos de cada pulsar, faz destes faróis cosmológicos relógios de precisão extrema e que, por isso, são usados como referências na navegação de sondas espaciais em viagens de longo curso.
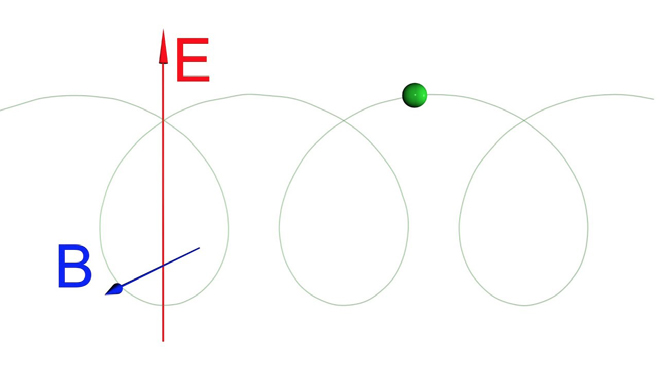
A FIGURA 3 representa o movimento de uma partícula carregada sob ação de campos elétrico (segundo \(y\)) e magnético (segundo \(z\)) uniformes e ortogonais. As equações de movimento ficam:
\(\frac{dv_{x}}{dt}=\frac{qB}{m}v_{y}\)
\(\frac{dv_{y}}{dt}=\frac{q}{m}\left ( E-v_{x}B \right )\) (4)
\(\frac{dv_{z}}{dt}=0\)
É interessente observar que o movimento será retilíneo e uniforme, com a velocidade \(v_{x}=\frac{E}{B}\) se a partícula entrar apenas com esta velocidade na região dos campos: o dispositivo tanto serve como seletor de velocidades como medidor das intensidades dos campos elétrico ou magnético. Para \(v_{x}\left ( 0 \right )\neq \frac{E}{B}\), a solução das equações de movimento, admitindo, para simplificar, \(v_{z}=0\), é:
\(v_{x}\left ( t \right )=\left [ v_{x}\left ( 0 \right )-\frac{E}{B} \right ]cos\left ( \omega _{c}t \right )+\frac{E}{B}\)
\(v_{y}\left ( t \right )=-\left [ v_{x}\left ( 0 \right )-\frac{E}{B} \right ]sen\left ( \omega _{c}t \right )\)
O movimento é plano e consiste na sobreposição de um movimento uniforme na direção perpendicular aos campos, com um movimento circular uniforme no plano perpendicular ao campo magnético (FIGURA 3).
No efeito Hall (FIGURA 4), uma corrente elétrica (intensidade \(I\)) atravessa longitudinalmente uma amostra de metal ou semicondutor.
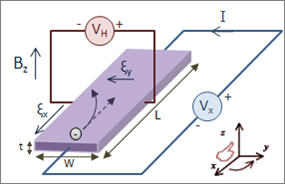
Os transportadores podem ter carga negativa (eletrões) ou positiva (vazios), são desviados por um campo magnético uniforme \(\left ( B_{z} \right )\) que os faz acumular numa das faces laterais até originarem um campo elétrico \(E_{y}-v_{x}B_{z}=0\) que anula a força de Lorentz na situação estacionária e define a tensão Hall \(V_{H}=E_{y}w=v_{x}B_{z}w\). O sinal deste campo depende do sinal de \(v_{x}\), o qual é definido pelo tipo de transportadores. Para eletrões, é \(I=-n_{e}\left | q_{e} \right |v_{x}wt\), onde \(n_{e}\) é a densidade eletrónica, pelo que \(V_{H}=-\frac{IB_{z}}{n_{e}\left | q_{e} \right |t}\); para vazios, obtém-se, de forma análoga, \(V_{H}=\frac{IB_{z}}{n_{v}\left | q_{e} \right |t}\), onde \(n_{v}\) é a densidade de vazios. Em qualquer caso, define-se a resistência Hall por \(R_{H}=\frac{\left | V_{H} \right |}{I}\) que, contudo, não é dissipativa, ao contrário da resistência habitual da amostra, origem da queda de tensão que acompanha a corrente. O efeito Hall é atualmente utilizado em sensores na medição de campos magnéticos.
Correntes elétricas em condutores retilíneos e paralelos (distantes \(a\)), atraem-se se tiverem o mesmo sentido e repelem-se se tiverem sentidos opostos (FIGURA 5).
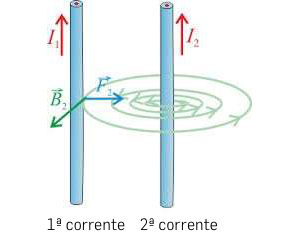
Com efeito, o campo magnético criado pela corrente \(I_{2}\) é2 \(\frac{B_{\phi }}{\mu_{0}}=\frac{I_{2}}{2\pi r}\) onde \(r\) é a distância ao eixo do segundo condutor, o qual se identificou com o eixo z de coordenadas cilíndricas. Este campo atua sobre a corrente \(I_{1}\) com a força de Laplace que, por unidade de comprimento daquele condutor, é:
\(\frac{d\vec{F}_{12}}{dl}=-I_{1}B_{\phi }\left ( a \right )\vec{e}_{r}=-\mu_{0}\frac{I_{1}I_{2}}{a}\vec{e}_{r}\) (5)
Assim, para \(I_{1}=I_{2}=1A\) e \(a = 1m)\), a força é atrativa valendo \(2\times 10^{-7}\frac{N}{m}\), resultado que serviu para definir a unidade de corrente até muito recentemente.
Se os fios condutores forem complanares, mas ortogonais (FIGURA 6), cada um experimenta agora uma distribuição de forças de resultante nula, mas de momento resultante não nulo que tende a rodar os fios de modo a ficarem paralelos.
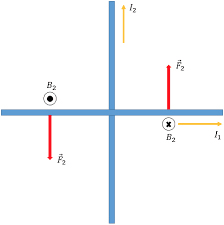
Na balança de correntes (FIGURA 7), um quadro de espiras retangulares, paralelas, é suspenso verticalmente do braço de uma balança.

O quadro é mergulhado na região entre polos de um íman, que cria um campo uniforme e horizontal \(\vec{B}_{a}\) perpendicular ao quadro. Se este for percorrido por uma corrente \(i\), a porção horizontal, de comprimento l, de cada espira experimenta a força vertical \(F_{z}=IlB_{a}\) que é medida através do peso acrescentado ao outro prato da balança para equilibrar. Este método permite, assim, determinar a intensidade da corrente ou do campo magnético do íman. Para um sistema de correntes localizadas numa região finita do espaço sob ação de um campo magnético aplicado \(\vec{B}^{\left ( a \right )}\), a resultante das forças é:
\(\vec{F}=\int dV\vec{i}\left ( \vec{r} \right )\wedge \vec{B}^{\left ( a \right )}\left ( \vec{r} \right )\)
Conclui-se imediatamente que se o campo aplicado for uniforme na região das correntes, esta resultante é nula. Escolha-se um ponto naquela região para origem do sistema de eixos cartesianos. Se o campo aplicado variar ligeiramente na região, tem-se:
\(\vec{F}=\int dV\vec{i}\left ( \vec{r} \right )\wedge \left ( \vec{r}\cdot \bigtriangledown \right )\vec{B}^{\left ( a \right )}\left ( 0 \right )\)
significando que as derivadas devem ser tomadas na origem. Considere-se, por exemplo, a componente \(F_{x}\) da força. Vem:
\(F_{x}=\int dV\left [ i_{y}\left ( \vec{r} \right )\left ( x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+z\frac{\partial }{\partial z} \right )B_{z}^{\left ( a \right )}-i_{z} \left ( \vec{r} \right )\left ( x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+z\frac{\partial }{\partial z} \right )B_{y}^{\left ( a \right )} \right ]\)
Ora2, o tensor \(\int dVi_{k}\left ( \vec{r} \right )x_{j}\) é anti-simétrico e os seus elementos não diagonais definem o momento magnético do sistema de correntes, por exemplo \(\int dVxi_{y}\left ( \vec{r} \right )=\mu _{z}\), obtendo-se as outras componentes por permutação circular. Deste modo, a expressão anterior fica:
\(F_{x}=\mu_{z}\frac{\partial B_{z}^{\left ( a \right )}}{\partial x}-\mu_{x}\frac{\partial B_{z}^{\left ( a \right )}}{\partial z}+\mu_{y}\frac{\partial B_{y}^{\left ( a \right )}}{\partial x}-\mu_{x}\frac{\partial B_{y}^{\left ( a \right )}}{\partial y}\)
Atendendo a que \(\bigtriangledown \cdot\vec{B}^{\left ( a \right )}=0\), os termos que multiplicam \(\mu_{x}\) dão \(\mu_{x}\frac{\partial B_{x}^{\left ( a \right )}}{\partial x}\), obtendo-se a expressão final:
\(F_{x}=\mu_{x}\frac{\partial B_{x}^{\left ( a \right )}}{\partial x}+\mu_{y}\frac{\partial B_{y}^{\left ( a \right )}}{\partial x}+\mu_{z}\frac{\partial B_{z}^{\left ( a \right )}}{\partial x}=\vec{\mu}\cdot \frac{\partial \vec{B}^{\left ( a \right )}}{\partial x}\) (6)
Analogamente se obtém as outras componentes.
Na experiência de Stern-Gerlach (1922), um feixe colimado de iões de prata entra numa região onde existe um campo magnético não homogéneo com \(\frac{\partial B_{z}^{\left ( a \right )}}{\partial z}\) constante (FIGURA 8).
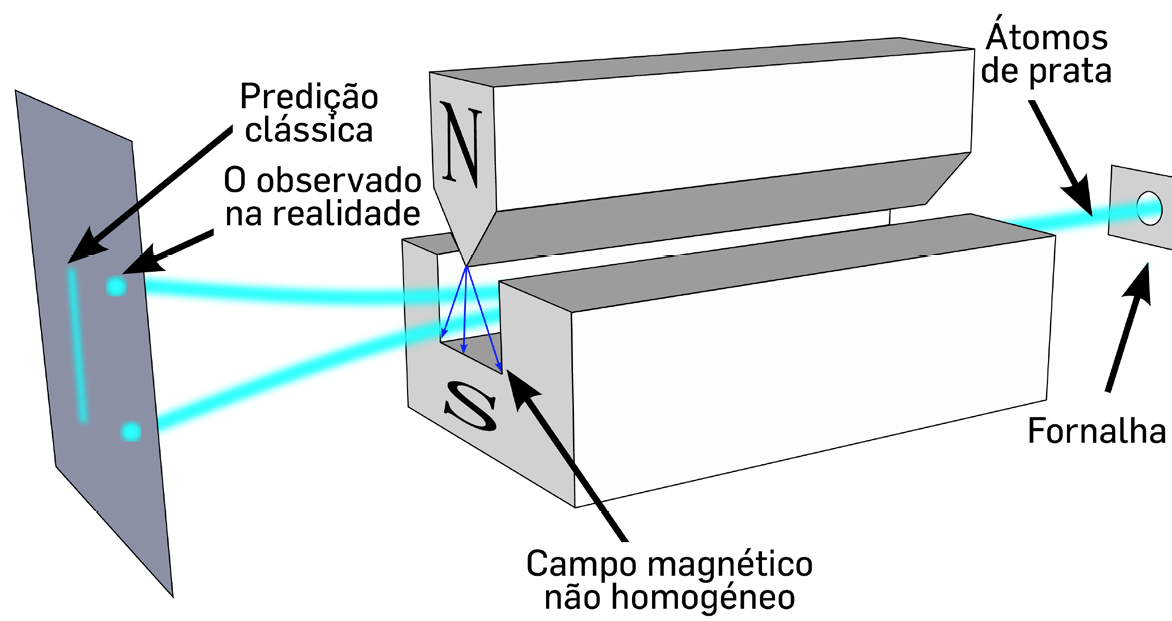
Os iões têm um momento magnético devido ao eletrão solitário no estado \(5s^1\). Assim, são atuados pela força \(F_{z}=\mu_{z}\frac{\partial B_{z}^{\left ( a \right )}}{\partial _{z}}\). Em Física Clássica, \(\mu_{z}\) poderia ter qualquer valor entre \(\pm \mu_{B}\) (\(\mu_{B}\) é o magnetão de Bohr2), prevendo-se, então, uma distribuição contínua no alvo, mas não é isso que é observado. Com efeito, segundo a teoria quântica, é \(\vec{\mu}=-2\mu_{B}\vec{s}\) onde \(\vec{s}\) é o spin que só pode tomar os valores \(\pm \frac{1}{2}\) (em unidades de \(\frac{h}{2\pi}\)) em qualquer direção. Portanto, a previsão desta teoria é o feixe dividir-se em dois, porque \(F_{z}=\pm \mu _{B}\frac{\partial B_{z}^{\left ( a \right )}}{\partial z}\), originando, apenas, dois “pontos” no alvo, o que é confirmado pela experiência, uma demonstração inequívoca do spin do eletrão.
Defina-se a energia de interação magnética, designando, agora, por \(\vec{r}\) a posição da origem escolhida no sistema de correntes em relação a uma origem fixa no laboratório:
\(U\left ( \vec{r} \right )=-\mu \cdot\vec{B}^{\left ( a \right )}\left ( \vec{r} \right )\) (7)
Se se deslocar rigidamente o sistema de correntes de \(\delta \vec{u}=\delta u\vec{e}_{x}\), a variação desta energia é:
\(dU=-\vec{\mu}\cdot \left [ \vec{B}^{\left ( a \right )}\left ( \vec{r}+\delta \vec{u} \right ) -\vec{B}^{\left ( a \right )}\left ( \vec{r}' \right ) \right ]=-\vec{\mu}\cdot\frac{\partial \vec{B}^{\left ( a \right )}}{\partial x}\delta u\)
Ora, o trabalho realizado pelas forças do campo neste deslocamento é:
\(\delta W=F_{x}\delta u\)
com \(F_{x}\) determinado na eq. (6). Deste modo, tem-se:
\(\delta W=-dU\)
Imagine-se, agora, uma rotação rígida3 do sistema de correntes definida por \(\delta \vec{\Omega }\). Nestas condições, o momento magnético alterou-se de \(\delta \vec{u}=\delta \vec{\Omega }\wedge \vec{\mu}\), originando \(dU=-\delta \vec{\mu}\cdot\vec{B}^{\left ( a \right )}=-\left ( \delta \vec{\Omega }\wedge \vec{\mu} \right )\cdot \vec{B}^{\left ( a \right )}=-\left ( \vec{\mu}\wedge \vec{B}^{\left ( a \right )} \right )\cdot \delta \vec{\Omega }\).
Por outro lado, o trabalho realizado pelas forças escreve-se \(\delta W=\vec{M}\cdot \delta \vec{\Omega }\) onde \(\vec{M}\) é o momento das forças. Então, pela relação anterior entre trabalho e variação da energia magnética, obtém-se:
\(\vec{M}=\vec{\mu}\wedge \vec{B}^{\left ( a \right )}\) (8)
As equações (6) e (8) são análogas às obtidas para um dipolo elétrico4. Um dipolo magnético abandonado livremente tende a orientar-se paralelamente ao campo aplicado e a mover-se para onde o campo é mais intenso, em ambos os casos procurando minimizar a energia de interação magnética, eq. (7). O movimento de limalhas de ferro nas proximidades de um íman exemplifica bem estes resultados (FIGURA 9).

Usando a eq. (7) e considerando que o campo aplicado tem origem noutro dipolo magnético2, obtém-se a energia de interação entre dipolos:
\(U=-\frac{\mu_{0}}{4\pi}\frac{3\vec{\mu}_{2}\cdot\left ( \vec{r}_{2}-\vec{r}_{1} \right )\vec{\mu}_{1}\cdot\left ( \vec{r}_{2}-\vec{r}_{1} \right )-\vec{\mu}\cdot\vec{1}\left | \vec{r}_{2}-\vec{r}_{1} \right |^{2}}{\left | \vec{r}_{2}-\vec{r}_{1} \right |^{5}}-\frac{\mu_{0}}{4\pi}\vec{\mu}_{2}\cdot\vec{\mu}_{1}\delta \left ( \vec{r}_{2}-\vec{r}_{1} \right )\) (9)
O último termo só existe se os dois dipolos estiverem sobrepostos – tal acontece, por exemplo, na interação magnética eletrão-protão no hidrogénio, ambos possuidores de momentos magnéticos intrínsecos. Tal termo levanta a degenerescência de spin no estado \(1s\) (porque a função de onda deve ser não nula no núcleo), originando a linha de 21 cm identificadora do hidrogénio em Cosmologia. Ignorando este termo, a energia de interação entre dipolos magnéticos é inteiramente semelhante à energia de interação entre dipolos elétricos.
Um supercondutor (do tipo \(I\)) expele qualquer campo magnético do seu interior (efeito Meissner). Assim, se se aproximar um magneto do supercondutor, são geradas correntes superficiais que anulam o campo no seu interior, originando um campo, no exterior, que repele o magneto fazendo-o levitar (FIGURA 10).

Um modelo simples que captura o essencial desta experiência, consiste em considerar um dipolo magnético a uma certa distância da superfície plana e horizontal de um supercondutor (FIGURA 11).
O anulamento do campo no interior deste, exige que seja nula a componente vertical do campo magnético imediatamente no acima da superfície. O método das imagens5 permite, então, determinar o campo em toda a região acima da superfície e, dessa forma, calcular a força que se exerce sobre o dipolo. Para isso, começa-se por recordar a expressão do campo criado por um dipolo magnético:
\(\vec{B}\left ( \vec{r} \right )=\frac{\mu_{0}}{4\pi}\frac{3\left ( \vec{\mu}\cdot \vec{n} \right )\vec{n}-\vec{\mu}}{r^{3}}\)
Aqui, \(\vec{r}\) é a distância do dipolo ao ponto de observação e \(\vec{n}\) é um versor que aponta do dipolo para o mesmo ponto. Se o dipolo fizer um angulo \(\theta\) com a vertical, é imediato reconhecer que o dipolo-imagem deve estar à mesma distância do plano (azul na FIGURA 12) e fazer um ângulo \(\pi -\theta\) com a vertical (FIGURA 12).
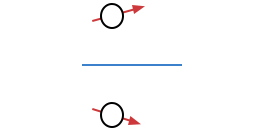
Usando a eq. (9), com o último termo obviamente ausente, a energia de interação entre os dois dipolos é:
\(U=\frac{\mu_{0}}{4\pi}\frac{\mu^{2}}{\left ( 2z \right )^{3}}\left [ 1+\left ( cos\theta \right )^{2} \right ]\)
onde \(z > 0\) é a cota do dipolo original (origem de coordenadas na interseção do eixo vertical que passa pelo dipolo, eixo \(x\) na interseção do plano definido pelo dipolo e a vertical). Esta energia é mínima para \(\theta=\frac{\pi}{2}\) (dipolos paralelos), o que se considera doravante. É, então, esta a energia para a FIGURA 11. Para obter a cota de equilíbrio, suponha-se que se desloca o dipolo de \(\delta z\); a sua imagem desloca-se em sentido contrário. O trabalho realizado pelas forças do campo é, então \(F_{z}\times 2\delta z=-dU\), i.e., \(F_{z}=-\frac{1}{2}\frac{\partial U}{\partial z}\). Esta força equilibra o peso mg do dipolo (\(m\) é a sua massa), obtendo-se, para a cota no equilíbrio \(z=\left [ \frac{3\mu_{0}\mu^{2}}{64\pi mg} \right ]^{\frac{1}{4}}\).
O campo imediatamente acima do supercondutor, reduz-se no plano à soma das componentes horizontais dos campos do dipolo e sua imagem; sendo nulo no supercondutor, há uma descontinuidade originada por correntes superficiais2:
\(i_{x}^{\left ( s \right )}\left ( x \right )=-\frac{\mu}{2\pi}\frac{1}{\left ( r'^{2}+z^{2} \right )^{\frac{3}{2}}}\frac{3r'^{2}\textrm{cos}\phi \textrm{sen}\phi}{r'^{2}+z^{2}}\)
\(i_{y}^{\left ( s \right )}\left ( x \right )=-\frac{\mu}{2\pi}\frac{1}{\left ( r'^{2}+z^{2} \right )^{\frac{3}{2}}}\left [\frac{3r'^{2}\left ( \textrm{cos}\phi \right )^{2}}{r'^{2}+z^{2}}-1 \right ]\)
Aqui, \(r'\) e \(\phi\) são coordenadas polares no plano e z é a cota atrás obtida. São estas correntes que determinam o efeito Meissner.
O trabalho da força de Laplace
A FIGURA 13 representa uma espira, não necessariamente plana, percorrida por uma co rente constante \(I\) cujo sentido define o sentido da circulação na espira de que \(d\vec{l}\) é um pequeno vetor, tangente à espira e de grandeza igual ao elemento de comprimento naquela linha, ficando, assim, também definida a normal unitária à superfície (em estriado azul) que nela se apoia. A espira desloca-se no espaço onde reside um campo magnético estacionário \(\vec{B}\) (linhas de força a vermelho). Cada ponto da espira sofre um deslocamento \(\vec{w}\) (linhas negras), não necessariamente uniforme. Deste modo, fica construído um cilindro deformado do qual a base inferior é a superfície que se apoia na espira na sua posição inicial e a base superior é a superfície que se apoia na espira na sua posição final, sendo a superfície lateral do cilindro definida pelo campo de deslocamentos. Note- -se que o sentido da circulação determina (regra do saca-rolhas) o sentido da normal em cada base: este aponta para o exterior do cilindro na base superior e para o seu interior na base inferior.
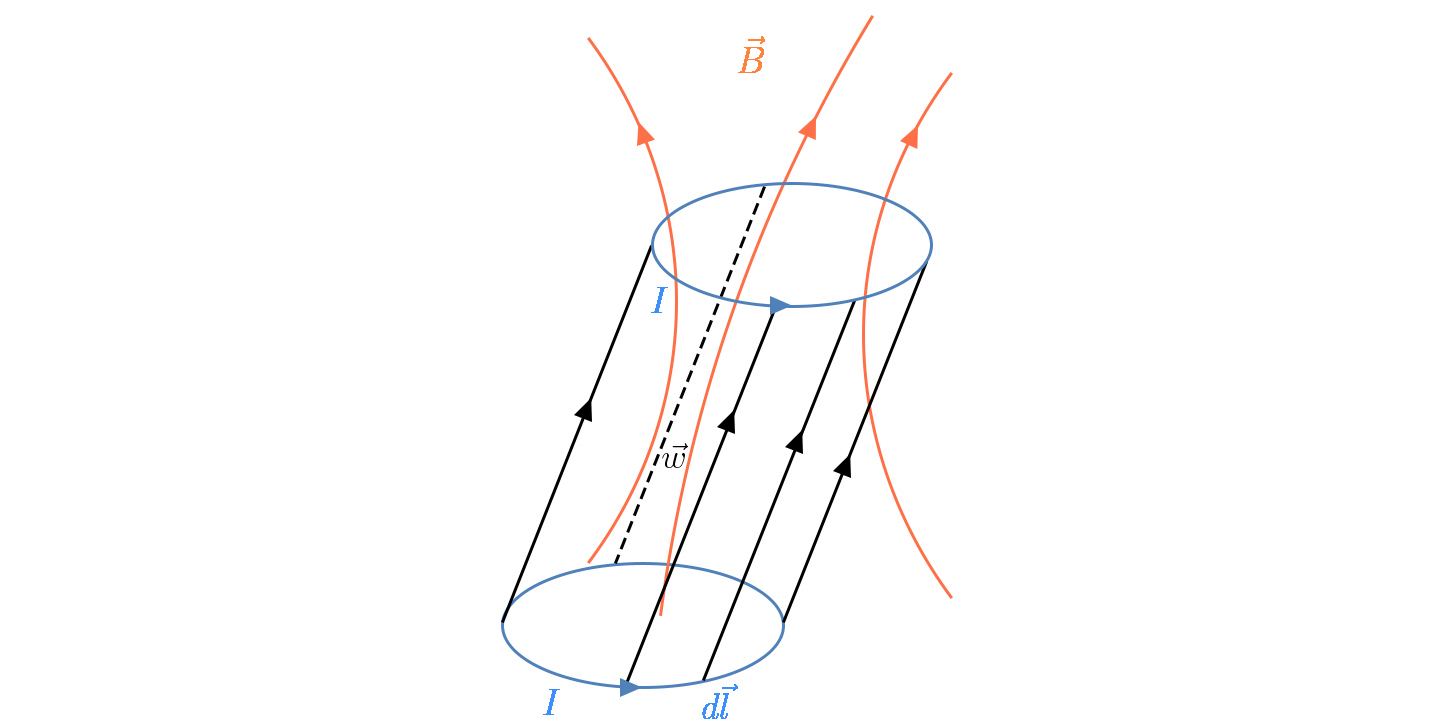
Na superfície lateral, o pequeno vetor \(d\vec{l}\wedge \vec{w}\) aponta para o exterior do cilindro e a sua grandeza é o elemento de área nesta superfície. Ora, a força de Laplace que atua sobre o elemento \(d\vec{l}\) é \(Id\vec{l}\wedge \vec{B}\), pelo que o trabalho realizado no deslocamento fica: \(Id\vec{l}\wedge \vec{B}\cdot\vec{w}=-Id\vec{l}\wedge \vec{w}\cdot \vec{B}\), o que, somado ao longo do circuito, dá \(-I\oint d\vec{l}\wedge \vec{w}\cdot\vec{B}\), i.e., o produto da corrente pelo fluxo do campo magnético através da superfície lateral do cilindro e para o seu interior. Ora, o fluxo do campo através de todo o cilindro é nulo, pelo que aquele fluxo iguala a diferença \(\delta \Phi \) dos fluxos entre a base superior e a base inferior. Mais simplesmente, \(\delta \Phi \) é a variação do fluxo através da espira. Resumindo: o trabalho realizado pelas forças de Laplace no deslocamento do circuito é:
\(\delta W_{L}=I\delta \Phi \) (10)
Este resultado é muito útil e reproduz facilmente algumas conclusões anteriores. Por exemplo, se a espira for muito pequena, envolvendo uma área \(S\), tem-se: \(I\Phi =IS\vec{n}\cdot \vec{B}=\vec{\mu}\cdot\vec{B}\), onde \(\vec{\mu}\) é o momento magnético, pelo que o trabalho numa translação da espira, é \(\delta W=\vec{\mu}\cdot\delta \vec{B}\), como atrás se encontrou.
A eq. (10) merece alguns comentários adicionais. Com efeito, é sabido que o campo magnético não realiza trabalho, o que parece estar em contradição com aquela equação. Ora, ao deslocar-se através do campo magnético. A mesma variação de fluxo gera (Faraday) uma força eletromotriz \(\varepsilon =-\frac{d\Phi }{dt}\), portanto, uma potência \(I\varepsilon\) que, integrada no intervalo de tempo do deslocamento, é:
\(\delta W_{F}=-I\delta \Phi \) (11)
(Lembra-se que a corrente é mantida constante). Este “trabalho de Faraday” compensa exactamente o “trabalho de Laplace” e, na verdade, existe um outro “trabalho de Faraday”, igual ao anterior, porque, no seu deslocamento o campo magnético da espira faz variar o fluxo no circuito que gera o campo magnético que a espira atravessou. A soma destes três trabalhos do campo eletromagnético corresponde à diminuição da energia magnética em todo o espaço, conforme se discutiu em “Os fundamentos do eletromagnetismo” e se voltará a discutir a propósito da lei de indução de Faraday.
Um comentário final sobre a força de Lorentz como origem das eqs. (10) e (11). Voltando à FIGURA 13, designe-se por \(\vec{v}\) a velocidade das cargas ao longo da espira e por \(\vec{V}\) a sua velocidade na translação da espira. Para cada carga, a força de Lorentz é \(q\left ( \vec{v}+\vec{V} \right )\), sendo, evidentemente, nula a sua potência:
\(0=\left ( \vec{v}+\vec{V} \right )\wedge \vec{B}\cdot\left ( \vec{v}+\vec{V} \right )=\vec{v}\wedge \vec{B}\cdot\vec{V}+\vec{V}\wedge \vec{B}\cdot\vec{v}\)
Se \(n\) for o número de transportadores por unidade de comprimento da espira, a intensidade da corrente é \(I=nq\left | \vec{v} \right |\). Multiplicando por \(nqdl\) a identidade acima, substituindo \(nq\vec{v}dl\) por \(Id\vec{l}\) e integrando ao longo da espira, obtém-se:
\(I\oint d\vec{l}\wedge \vec{B}\cdot \vec{V}+I\oint \vec{V}\wedge \vec{B}\cdot d\vec{l}=0\)
O primeiro termo é a potência da força de Laplace para a translação da espira; o segundo termo é a potência da indução de Faraday na espira (\(\vec{V}\wedge \vec{B}\) é a força de Lorentz sobre a unidade de carga que, por integração ao longo da espira, é a força eletromotriz). Ficará, assim, mais claro por que os dois trabalhos são iguais e de sinais opostos.
Uma discussão mais completa e profunda da lei de Faraday deverá ocupar um outro trabalho.
Referências
- 1 LAGE, E., O sólido rígido, Rev. Ciência Elem., V8(3):044. (2020). DOI: 10.24927/rce2020.044.
- 2 LAGE, E., Imagens elétricas e o método de separação de varíaveis, Rev. Ciência Elem. no prelo.
Este artigo já foi visualizado 6622 vezes.



